Содержание
- 2. Эпиграф Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда
- 3. Доказать одно из свойств арифметических прогрессий и воспользоваться им на практике. Цель исследовательской работы:
- 4. Арифметическая прогрессия - это последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним
- 5. 7.32. 1) Найдите сумму первых 20 совпадающих членов двух арифметических прогрессий: 3, 8, 13, … и
- 6. Первый совпадающий член двух данных прогрессий можно найти, непосредственно выписав несколько последовательных членов каждой из них.
- 7. 1) НОК(Наименьшим общим кратным) натуральных чисел а и b называют наименьшее натуральное число, которое кратно и
- 8. Если а : b и а : c a : b x c НОК(Ra; Rb) =
- 9. Дано: (аn) и (bn) – арифметические прогрессии, соответственно с разностями d1 и d2, НОД(d1;d2) = 1;
- 10. См d = c2 – c1 = al – aR = a1 – a1 + d1(l
- 11. См примеры: 1) 12 : 4 12 = НОК(4; 3);см НОД(4;3) = 1 12 : 3
- 12. Примечание: Свойство НОК: Если а и b – не взаимно простые числа, НОК(Ra; Rb) = RНОК(а;
- 13. 7.32. 1)Найдите сумму первых 20 совпадающих членов двух арифметических прогрессий: 3, 8, 13, … 4, 11,
- 14. 3) d1 = a2 – a1 = 8 – 3 = 5 d2 = b2 –
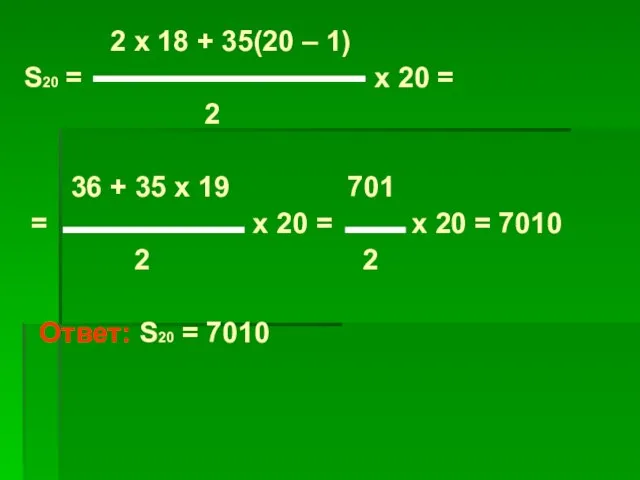
- 15. 2 x 18 + 35(20 – 1) S20 = x 20 = 2 36 + 35
- 16. 2) Найдите сумму первых 10 совпадающих членов двух арифметических прогрессий: 3, 7, 11, … и 1,
- 17. 3) d1 = a2 – a1 = 7 – 3 = 4 d2 = b2 –
- 18. 2 x 19 + 36(10 – 1) S10 = x 10 = 2 38 + 36
- 19. 12.98. В арифметической прогрессии 3; 6; 9; … содержится 463 члена, в арифметической прогрессии 2; 6;
- 20. 2) d1 = a2 – a1 = 6 – 3 = 3 d2 = b2 –
- 21. 5) сn = c1 + d(n – 1); n - ? 6 + 12(n – 1)
- 22. В заключении строки из романа А. С. Пушкина «Евгений Онегин», сказанные о его герое: «…Не мог
- 23. Ямб – стихотворный размер с ударениями на чётных слогах стиха (н: Мой дядя самых честных правил),
- 24. Хорей – стихотворный размер с ударением на нечётных слогах (н: Буря мглою небо кроет). Номера ударных
- 25. Практическая значимость 1)Моя работа может использоваться на уроках алгебры при изучении темы «Арифметические прогрессии». 2)Данное исследование
- 27. Скачать презентацию












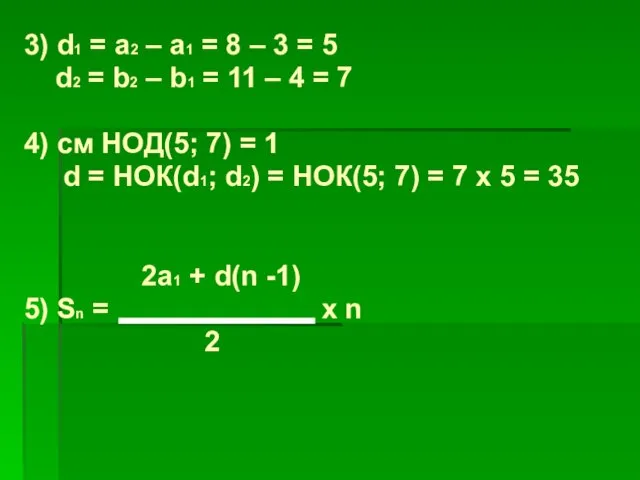










 О генномодифицированных продуктах
О генномодифицированных продуктах  Мой город Троицк
Мой город Троицк Крымские готы
Крымские готы ABBYY FineReader 10презентация продукта
ABBYY FineReader 10презентация продукта Склонение причастий.7 класс. Русский язык
Склонение причастий.7 класс. Русский язык lektsia_6
lektsia_6 курорты Кавказских минеральных вод- Драгоценные камни Юга России
курорты Кавказских минеральных вод- Драгоценные камни Юга России Итоговая годовая аттестация обучающихся
Итоговая годовая аттестация обучающихся День матери
День матери Компьютерный анализ естественно-языкового текста
Компьютерный анализ естественно-языкового текста Краеведческий музей МОУ лицей с.Верхний Мамон
Краеведческий музей МОУ лицей с.Верхний Мамон Финансовые рынки
Финансовые рынки Seven Wonders of the World
Seven Wonders of the World  Презентация на тему Вирусные Заболевание животных
Презентация на тему Вирусные Заболевание животных Презентация Лекция №2 (1)
Презентация Лекция №2 (1) Эффективные переговоры
Эффективные переговоры Как тебя зовут?
Как тебя зовут? Буровая сталь для шпуров малого диаметра
Буровая сталь для шпуров малого диаметра Аппликация из ватных дисков
Аппликация из ватных дисков Преступления против свободы, чести и достоинства
Преступления против свободы, чести и достоинства Творческая лаборатория «Методическая копилка»
Творческая лаборатория «Методическая копилка» Керлинг
Керлинг Международные event и MICE мероприятия
Международные event и MICE мероприятия Перемещение тела при прямолинейном равноускоренном движении без начальной скорости (по оси х)
Перемещение тела при прямолинейном равноускоренном движении без начальной скорости (по оси х) Различные виды деревьев в стихотворениях Сергея Есенина
Различные виды деревьев в стихотворениях Сергея Есенина Putzmeister. Новая версия
Putzmeister. Новая версия Византия
Византия Самовольная постройка
Самовольная постройка