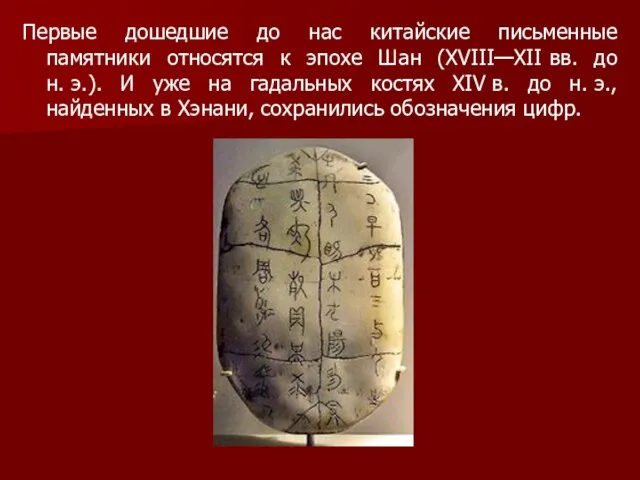
секторы круга, круговое кольцо . Операции с дробями. Алгоритм поиска наибольшего общего делителя двух чисел, аналогичный евклидовскому.
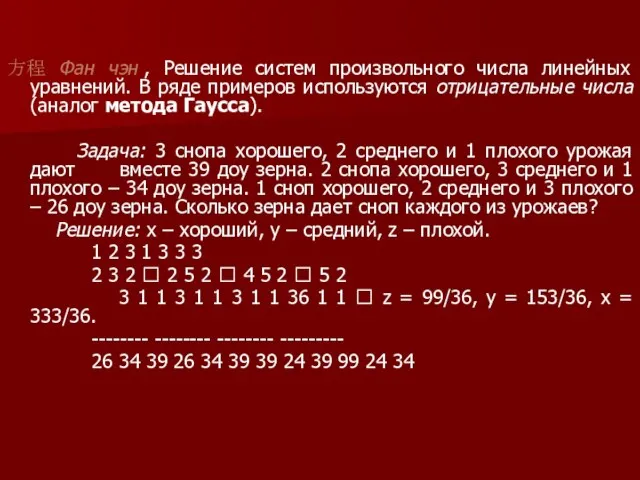
粟米 Су ми, «Соотношение злаков» — Правила обмена и торговли, в основном для зерновых культур (задачи на пропорции).
衰分 Шуай фэнь, «Деление по ступеням» — Пропорциональное распределение товара.
少廣 Шао гуан , Теория делимости. Извлечение квадратных и кубических корней. Измерение круга, сферы и шара.
商功 Шан гун, «Оценка работ» — Объёмы различных тел: параллелепипед, призма, пирамида, цилиндр, конус. Расчёт трудозатрат при строительстве.
均輸 Цзюнь шу, «Пропорциональное распределение» — Дополнительные сведения о пропорциональном распределении и задачи разного характера:бассейн, встречи, зерновые поставки, дальность перевозки и т.д..
Математика в девяти книгах
Каждая из 9 глав (книг) представляет собой завершённый текст, не ссылающийся на другие главы.









 Анненский Иннокентий Федорович
Анненский Иннокентий Федорович Экспертные советы по переходу на новую версию Microsoft SQL Server 2005
Экспертные советы по переходу на новую версию Microsoft SQL Server 2005 Мир в начале нового времени
Мир в начале нового времени Mark Zuckerberg
Mark Zuckerberg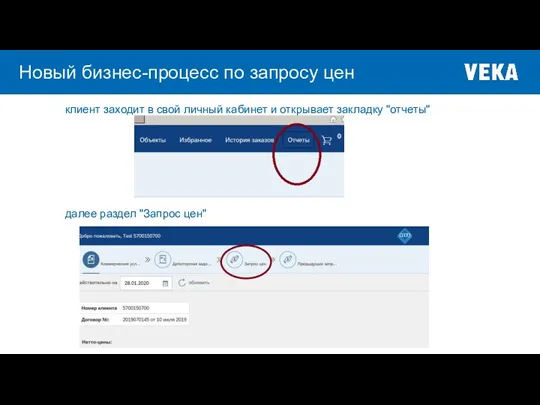 Новый бизнес-процесс по запросу цен
Новый бизнес-процесс по запросу цен Презентация на тему Глобальные мировые проблемы Сырьевая и энергетическая проблема мира
Презентация на тему Глобальные мировые проблемы Сырьевая и энергетическая проблема мира  Классификация магнитных материалов. Лекция 8
Классификация магнитных материалов. Лекция 8 Прецеденты. Вопросы, возникающие при определении исполнителей и задач. (Лекция 3)
Прецеденты. Вопросы, возникающие при определении исполнителей и задач. (Лекция 3) Действительные причастия прошедшего времени
Действительные причастия прошедшего времени Изучение математической модели иммунной защиты организма
Изучение математической модели иммунной защиты организма  Презентация на тему Измерение количества информации
Презентация на тему Измерение количества информации Мутационная изменчивость.
Мутационная изменчивость. МОУ гимназия №35 г.о. ТольяттиУчитель истории Егоров Вячеслав Валерьевич
МОУ гимназия №35 г.о. ТольяттиУчитель истории Егоров Вячеслав Валерьевич Разработка нового ассортимента кулинарной продукции из птицы и технологии их приготовления
Разработка нового ассортимента кулинарной продукции из птицы и технологии их приготовления Женское и мужское предпринимательство
Женское и мужское предпринимательство Методика проведения информированного добровольного тестирования учащихся на наличие наркотических и психотропных веществ
Методика проведения информированного добровольного тестирования учащихся на наличие наркотических и психотропных веществ Презентация на тему Тепловые электростанции
Презентация на тему Тепловые электростанции  0000c97f-4a15f5f3
0000c97f-4a15f5f3 Астрономические координаты
Астрономические координаты Поэзия 20 века о родной природе
Поэзия 20 века о родной природе Управление качеством образования на муниципальном уровне
Управление качеством образования на муниципальном уровне Бумажная филигрань Бумагокручение Квиллинг
Бумажная филигрань Бумагокручение Квиллинг Чувство Родины
Чувство Родины Модель регионального рынка электрической энергии – пилотный проект ЗАО «Энерговыбор»
Модель регионального рынка электрической энергии – пилотный проект ЗАО «Энерговыбор» Возвышение Москвы. Куликовская битва
Возвышение Москвы. Куликовская битва Содержание образования (литература)
Содержание образования (литература)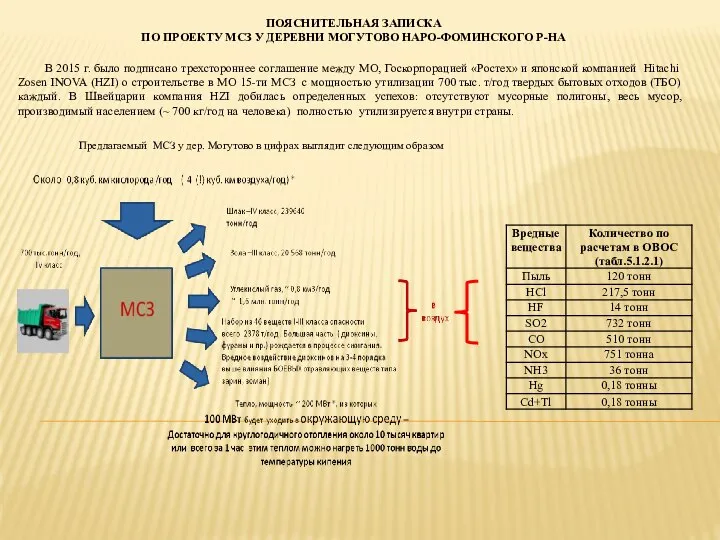 Пояснительная записка по проекту МСЗ у деревни Могутово Наро-Фоминского района
Пояснительная записка по проекту МСЗ у деревни Могутово Наро-Фоминского района Матрицы. Продавец. Инвестор. Помощник. Сетевик
Матрицы. Продавец. Инвестор. Помощник. Сетевик