Основные понятия теории автоматов

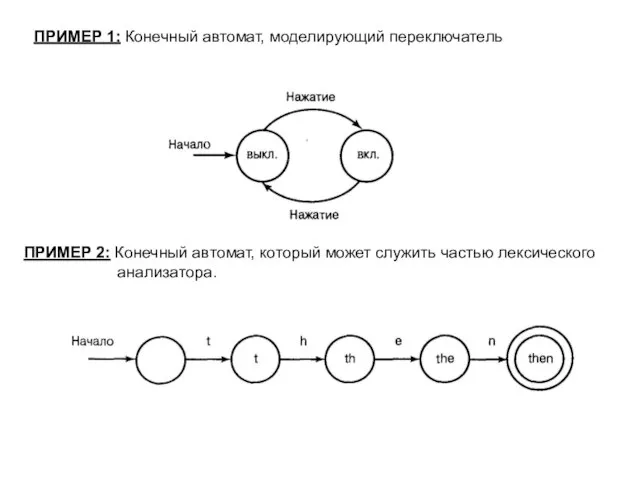
ПРИМЕР 1: Конечный автомат, моделирующий переключатель
ПРИМЕР 2: Конечный автомат, который может служить частью лексического анализатора.

Алфавитом называется конечное непустое множество символов.
Σ={0,1} – бинарный алфавит;
Цепочка в алфавите Σ – это конечная последовательность символов из Σ.
01101 – цепочка в бинарном алфавите;
Пустая цепочка ε - это цепочка, не содержащая символов. Можно рассматривать, как цепочку в любом алфавите.
Длиной цепочки х называется число различных вхождений символов в х.
Степень алфавита – определим Σk как множество всех цепочек длины k, состоящих из символов алфавита Σ.
Σ0={ε} независимо от алфавита;

Конкатенацией цепочек x и y называется цепочка xy.
Если цепочка имеет вид xyz, то x-префикс, y-подцепочка, z-суффикс.

Пусть I – алфавит. Регулярные выражения над I и языки, представляемые ими, рекурсивно определяются следующим образом:
∅ является регулярным выражением и представляет пустое множество.
ε является регулярным выражением и представляет множество {ε}.
Для каждого a∈I символ a является регулярным выражением и представляет множество {a}.
Если p и q – регулярные выражения, представляющие множества P и Q соответственно, то (p+q), (pq) и (p*) являются регулярными выражениями и представляют множества , и P* соответственно.

ПРИМЕР 1:
01 – регулярное выражение, представляющее множество {01}.
(0+1)* представляет {0,1}*.
1(0+1)*1+1 представляет множество всех цепочек, начинающихся и заканчивающихся символом 1.

Язык называется регулярным, если его можно представить регулярным выражением.
Два регулярных выражения α и β называют эквивалентными (и пишут α=β), если они представляют одно и то же множество.
Например, (0+1)*=(0*1*)*.

Языком над алфавитом Σ называют произвольное множество цепочек в Σ.
Пусть L1 и L2 – два языка. Язык L1L2, называемый конкатенацией L1 и L2, есть множество
Пусть L – язык. Тогда положим и при i≥1. Замыканием Клини
(итерацией) L* языка L называют язык
а позитивной итерацией L+ - язык

ПРИМЕРЫ ЯЗЫКОВ:

Язык представим регулярным выражением тогда и только тогда, когда он допускается некоторым конечным автоматом.
Недетерминированным конечным автоматом (НКА) называется пятёрка (S,I,δ,s0,F), где:
S – конечное множество состояний устройства управления;
I – алфавит входных символов;
δ - функция переходов, отображающая в множество подмножеств множества S;
- начальное состояние устройства управления;
- множество заключительных (допускающих состояний).

Мгновенным описанием (МО) НКА М называется пара (s,w), где s∈S – состояние блока управления и w∈I* - неиспользованная часть входной цепочки (т.е. символ, обозреваемый входной головкой, и все символы справа от него).
Начальным МО автомата М называется МО, у которого первой компонентой служит начальное состояние, а второй – распознаваемая цепочка, т.е. (s0,w) для некоторой цепочки w∈I*.

Допускающие МО – это МО вида (s,ε), где s∈F.
Представим шаги НКА бинарным отношением ├ на множестве мгновенных описаний. Если δ(s,a) содержит s/, то пишут (s,aw)├ (s/,w) для всех w∈I*(где a – это или ε, или символ из I).
Если a=ε, то состояние изменяется независимо от обозреваемого входного символа. Если a≠ε, то символ a должен стоять в очередной клетке входной ленты, а входная головка сдвигается на одну клетку вправо.

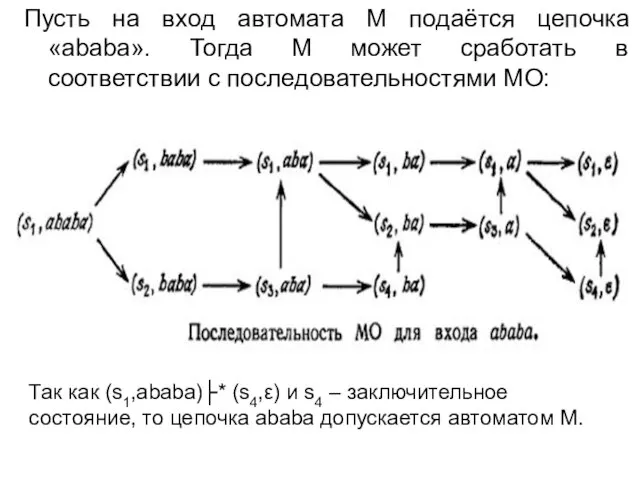
Рефлексивное и транзитивное замыкание отношения ├ обозначается через ├*.
Говорят, что цепочка w допускается автоматом М, если (s0,w)├* (s,ε) для некоторого s∈F. Иными словами, входная цепочка w допускается автоматом М, если найдётся последовательность из нуля или более шагов, переводящая М из начального МО (s0,w) в допускающее МО (s,ε).
Множество цепочек L(M), допускаемых автоматом М, называют языком, допускаемым автоматом М.

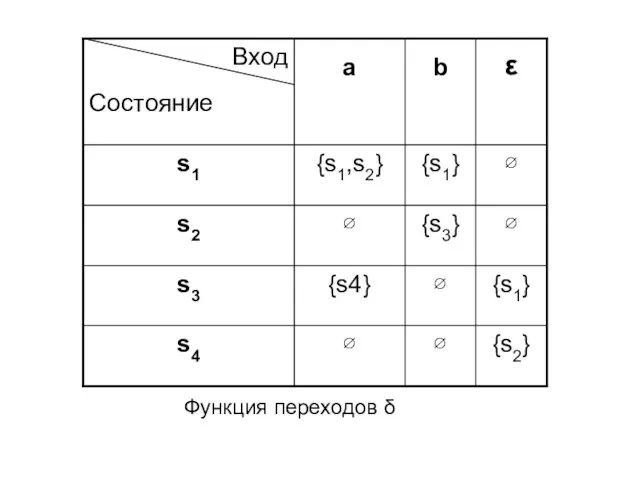
Пример 2:
Рассмотрим НКА М, допускающий все те цепочки из символов a и b, которые оканчиваются цепочкой «aba», т.е. L(M)=(a+b)*aba.
Пусть М=({s1,s2,s3,s4},{a,b},δ,s1,{s4}), где функция δ определена на рис. (без ε-переходов можно обойтись).

Функция переходов δ

Пусть на вход автомата М подаётся цепочка «ababa». Тогда М может сработать в соответствии с последовательностями МО:
Так как (s1,ababa)├* (s4,ε) и s4 – заключительное состояние, то цепочка ababa допускается автоматом М.

§2 Детерминированный конечный автомат
Детерминированный конечный автомат (ДКА) состоит из следующих элементов:

Способы описания автоматов:
Диаграмма переходов, которая представляет собой граф.
Таблица переходов, дающая табличное представление функции δ. Из неё очевидны состояния и входной алфавит.