Содержание
- 2. История открытия теоремы Обычно открытие теоремы Пифагора приписывают древнегреческому философу и математику Пифагору (VI в. до
- 3. Способы доказательства теоремы Пифагора Да, путь познания не гладок. Но знайте вы со школьных лет: Загадок
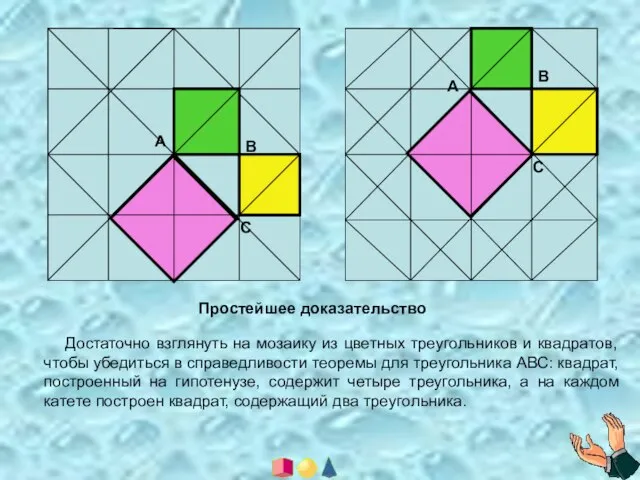
- 4. А В С А В С Простейшее доказательство Достаточно взглянуть на мозаику из цветных треугольников и
- 5. С2 b2 a2 а а а а а а а а b b b b b
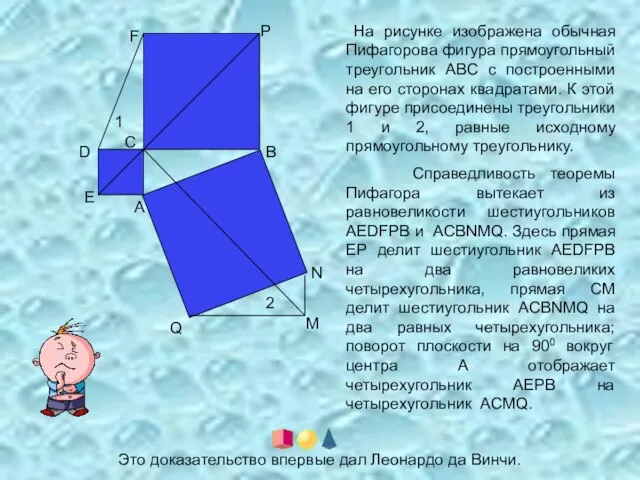
- 6. 1 2 A B C D E F P N M Q На рисунке изображена обычная
- 7. А В С D F E a b c Оригинальное доказательство, предложенное Гофманом. Здесь треугольник АВС
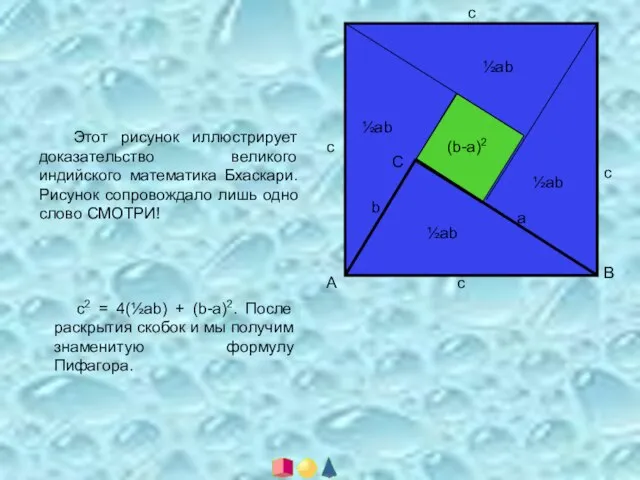
- 8. с с с с ½ab ½ab ½ab ½ab (b-a)2 A B C b a Этот рисунок
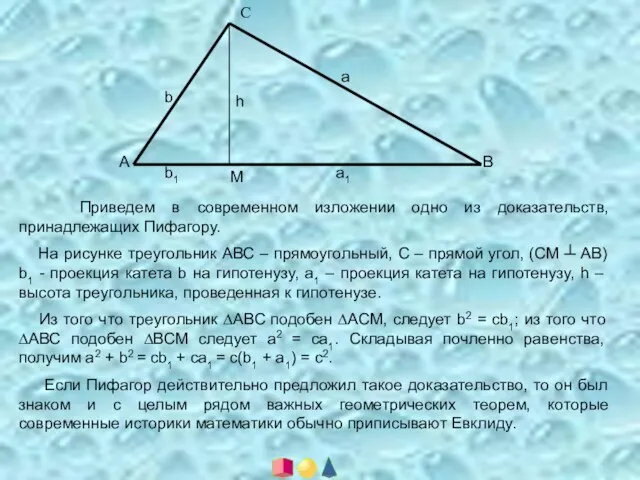
- 9. А С В h M b1 a1 a b Приведем в современном изложении одно из доказательств,
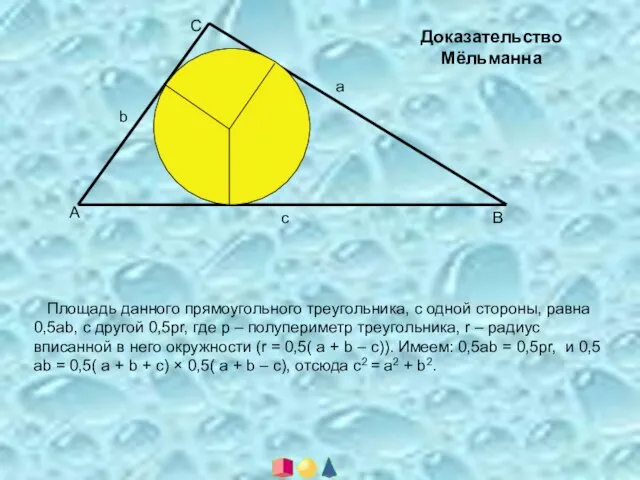
- 10. А В С а с b Доказательство Мёльманна Площадь данного прямоугольного треугольника, с одной стороны, равна
- 11. а а с с b b Доказательство Гарфилда На рисунке три прямоугольных треугольника составляют трапецию. Поэтому
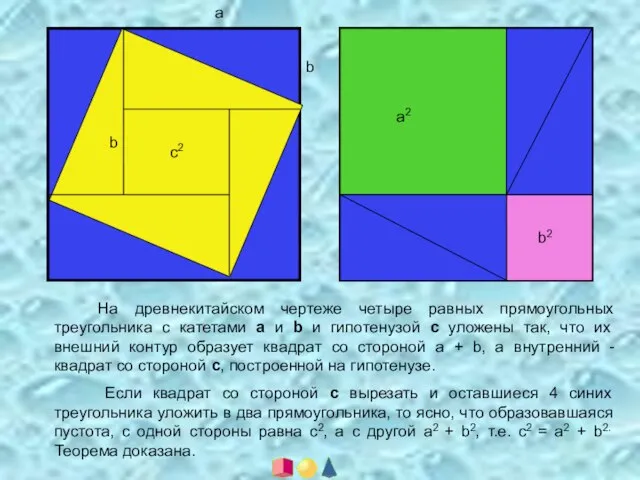
- 12. с2 а b а2 b2 На древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а и
- 13. Чертёж воспроизведен из трактата «Чжоу –би…». Здесь теорема Пифагора рассмотрена для египетского треугольника с катетами 3,
- 14. с с с с с с b b а - b b2 Математики Древней Индии заметили,
- 16. Скачать презентацию







 Промышленные инновации: азотовит, фосфатовит, микробиологические удобрения
Промышленные инновации: азотовит, фосфатовит, микробиологические удобрения Крестьянство и казачество. Экономическое положение губернии
Крестьянство и казачество. Экономическое положение губернии Развитие речи 2 класс
Развитие речи 2 класс Медиаполитика. Силы влияния демократического управления СМИ
Медиаполитика. Силы влияния демократического управления СМИ Штамповка заготовок на молотах
Штамповка заготовок на молотах Сказка как вид народной прозы
Сказка как вид народной прозы Полоролевое развитие детей старшего дошкольного возраста
Полоролевое развитие детей старшего дошкольного возраста Окрашивание бровей
Окрашивание бровей Компьютерные вирусы -
Компьютерные вирусы - Зачетная работа по дисциплинам Психология и Деловая культура. Тема: блюда, похожие на мой характер
Зачетная работа по дисциплинам Психология и Деловая культура. Тема: блюда, похожие на мой характер Погружение в проект. (Тема 3)
Погружение в проект. (Тема 3) Арт-терапия предпринимательства. Денежные вопросы для самоисследования
Арт-терапия предпринимательства. Денежные вопросы для самоисследования Новоиерусалимский монастырь
Новоиерусалимский монастырь Исследование ВСМС «Реальное состояние бюджетной обеспеченности муниципальных образований и предложения по улучшению финансов
Исследование ВСМС «Реальное состояние бюджетной обеспеченности муниципальных образований и предложения по улучшению финансов Самое большое насекомое в мире
Самое большое насекомое в мире Микроструктура феррито-перлитной стали
Микроструктура феррито-перлитной стали Лаборатория планирования и тайм-менеджмента
Лаборатория планирования и тайм-менеджмента Питание детей старше года
Питание детей старше года a406c9621711cd13461f61a6d5880de120151015-3-1kgg8mt
a406c9621711cd13461f61a6d5880de120151015-3-1kgg8mt Векторы
Векторы Белки - полимеры
Белки - полимеры Окна. Работа с окнами. Панель инструментов.Гладуненко Любовьгруппа 1Г4
Окна. Работа с окнами. Панель инструментов.Гладуненко Любовьгруппа 1Г4 Название команды
Название команды Линейное руководство: Виды влияния
Линейное руководство: Виды влияния Презентация на тему Предлоги Английского языка
Презентация на тему Предлоги Английского языка Презентация на тему Аварии на радиационных объектах
Презентация на тему Аварии на радиационных объектах  Изменение агрегатных состояний вещества. Испарение
Изменение агрегатных состояний вещества. Испарение Обследование и реконструкция сетей и сооружений систем водного хозяйства (Лекция 3)
Обследование и реконструкция сетей и сооружений систем водного хозяйства (Лекция 3)