Переход Андерсона:теория и численный экспериментИ.М.СусловИнститут физических проблем им. П.Л.Капицы РАН
Содержание
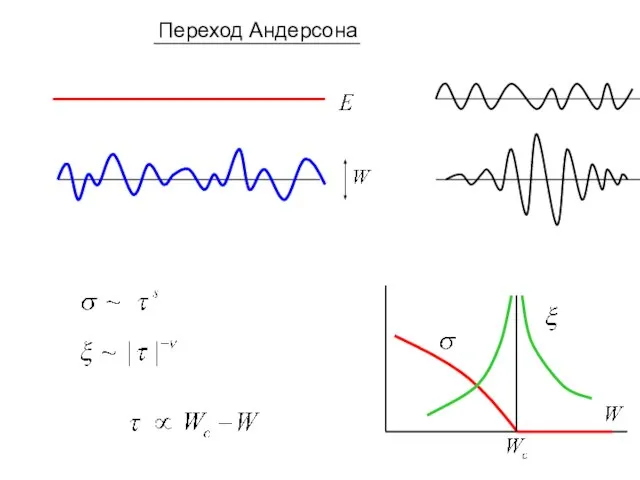
- 2. Переход Андерсона
- 3. Современная ситуация: Численный счет противоречит всей прочей информации о критическом поведении Numerical analysis of the Anderson
- 4. Самосогласованная теория Вольхардта-Вольфле дает результат который: (а) выделяет значения dc1=2 и dc2=4 как верхнюю и нижнюю
- 5. Гипотеза о том, что результаты теории Вольхардта-Вольфле являются точными: Вывод без грубых аппроксимаций:
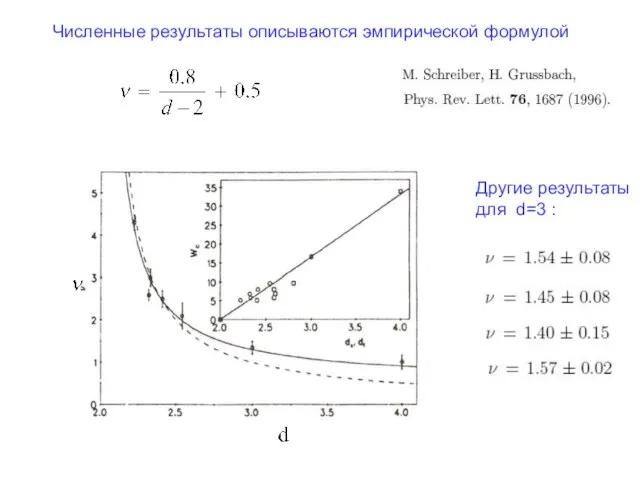
- 6. Численные результаты описываются эмпирической формулой Другие результаты для d=3 :
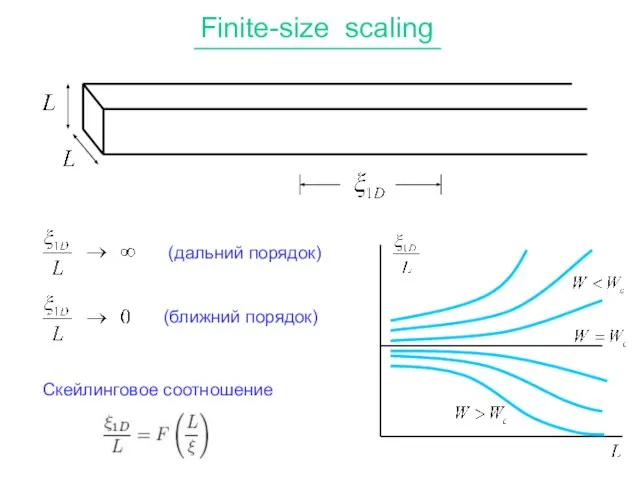
- 7. Finite-size scaling (дальний порядок) (ближний порядок) Скейлинговое соотношение
- 8. Теория Вольхардта-Вольфле Основана на существовании диффузионного полюса в неприводимой четыреххвостке играющей роль вероятности перехода в квантовом
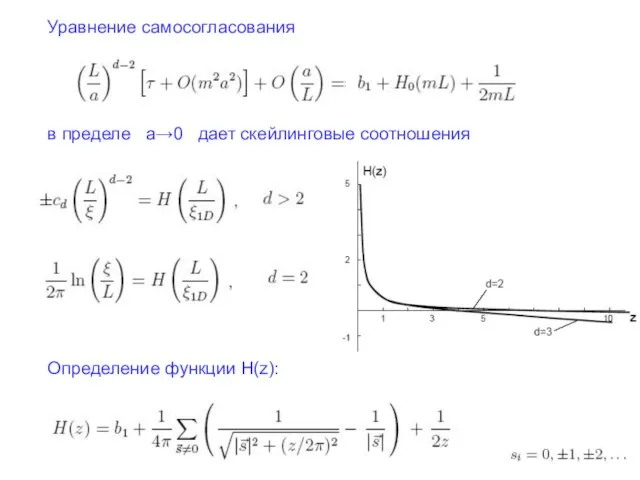
- 9. Уравнение самосогласования Базовый интеграл конечен при m=0 только для d>2. Металлическая фаза: D=const при ω→ 0
- 10. Уравнение самосогласования Диэлектрическая фаза: D = - iω ξ2 при ω→ 0 ( m=ξ-1 )
- 11. Квазиодномерные системы Для описания квазиодномерных систем базовый интеграл достаточно представить в виде ( ) : Член
- 12. Преобразование интегралов: что надо подставить в уравнение самосогласования
- 13. Уравнение самосогласования в пределе a→0 дает скейлинговые соотношения Определение функции H(z):
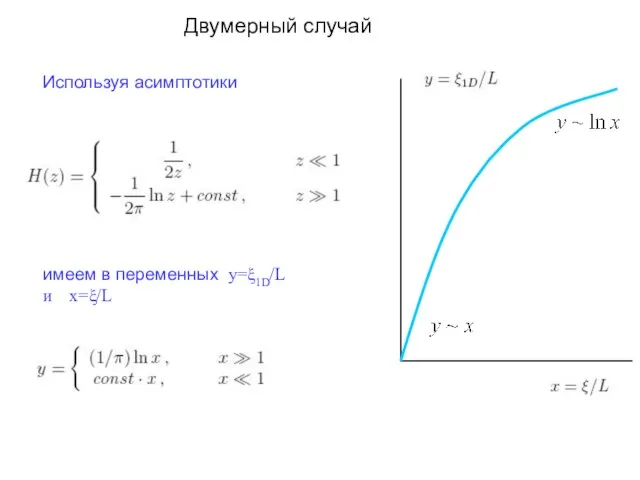
- 14. Двумерный случай Используя асимптотики имеем в переменных y=ξ1D/L и x=ξ/L
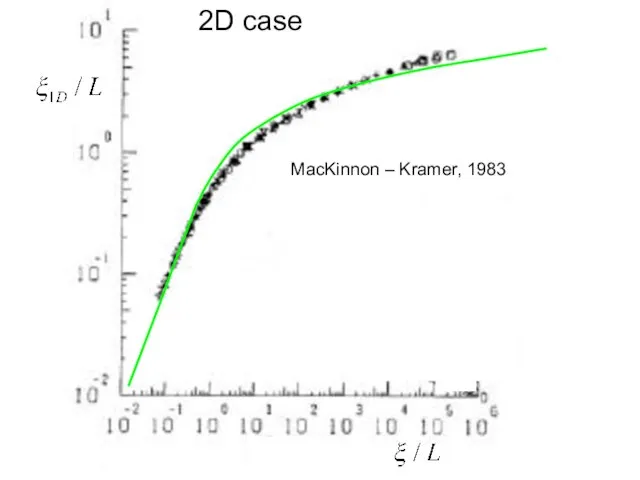
- 15. MacKinnon – Kramer, 1983 2D case
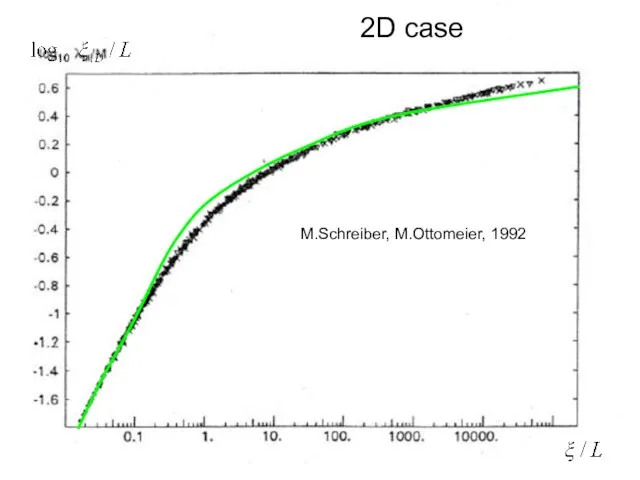
- 16. 2D case M.Schreiber, M.Ottomeier, 1992
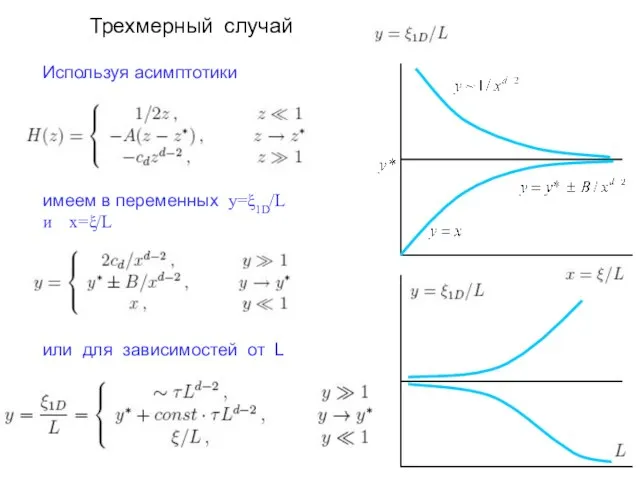
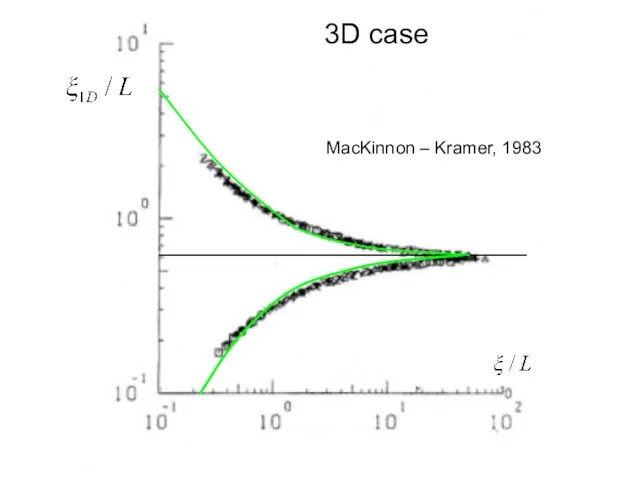
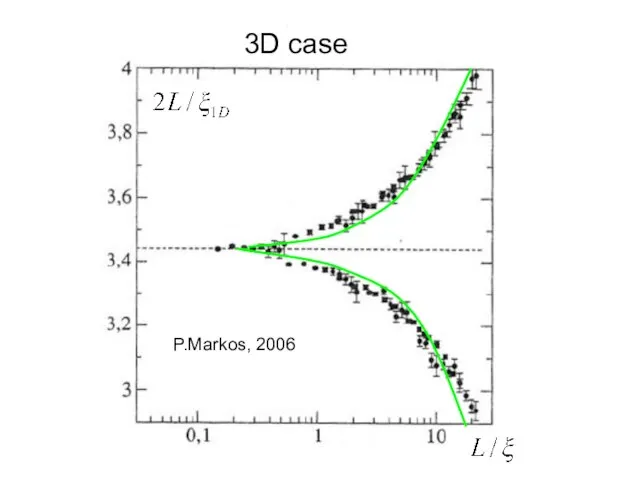
- 17. Трехмерный случай Используя асимптотики имеем в переменных y=ξ1D/L и x=ξ/L или для зависимостей от L
- 18. MacKinnon – Kramer, 1983 3D case
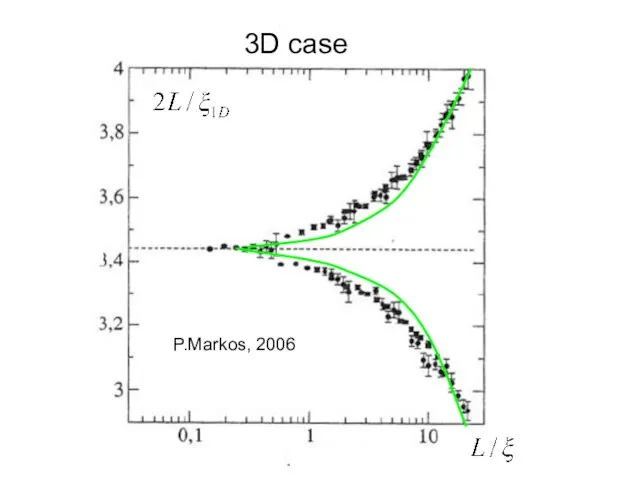
- 19. P.Markos, 2006 3D case
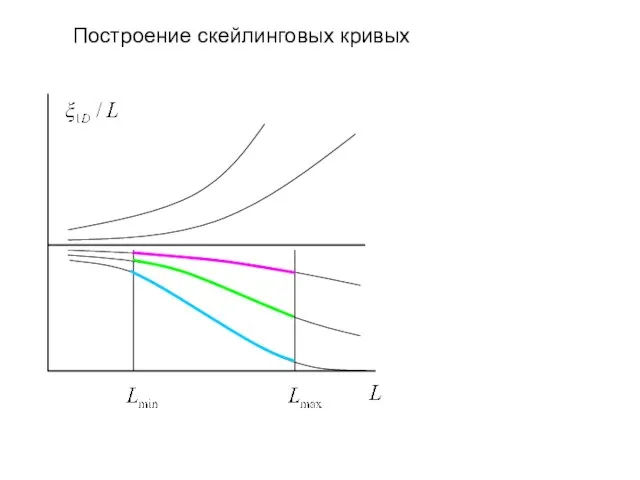
- 20. Построение скейлинговых кривых
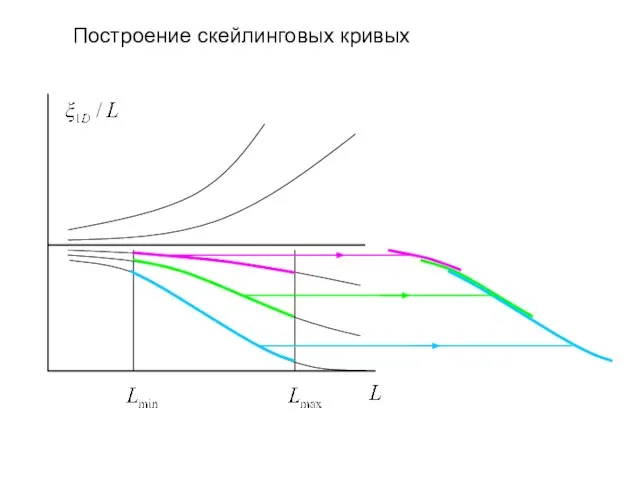
- 21. Построение скейлинговых кривых
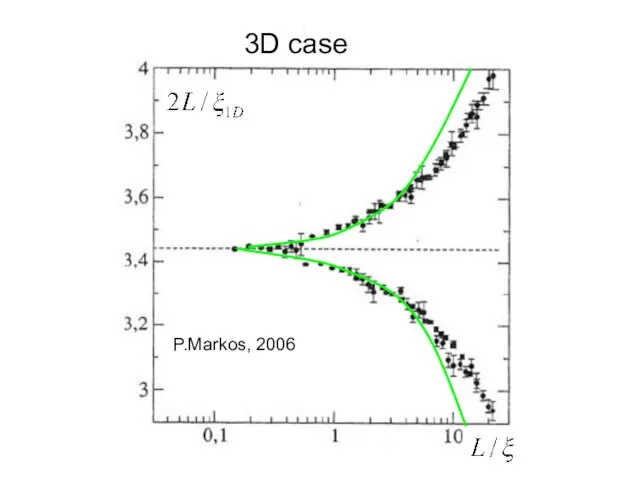
- 22. P.Markos, 2006 3D case
- 23. P.Markos, 2006 3D case
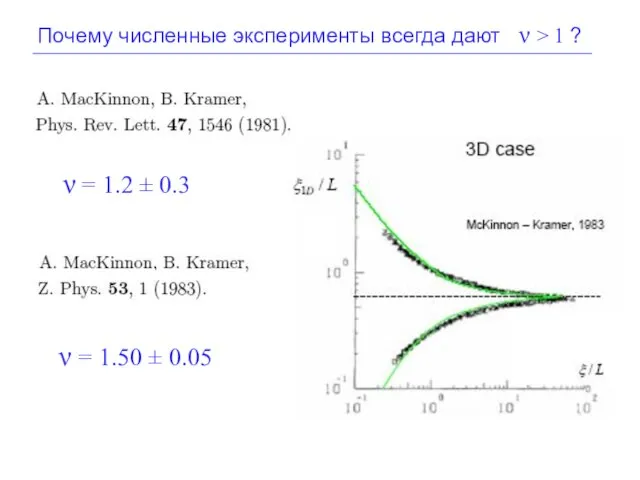
- 24. Почему численные эксперименты всегда дают ν > 1 ? ν = 1.2 ± 0.3 ν =
- 25. Ситуация в окрестности перехода Стандартные представления: На самом деле: В общем случае:
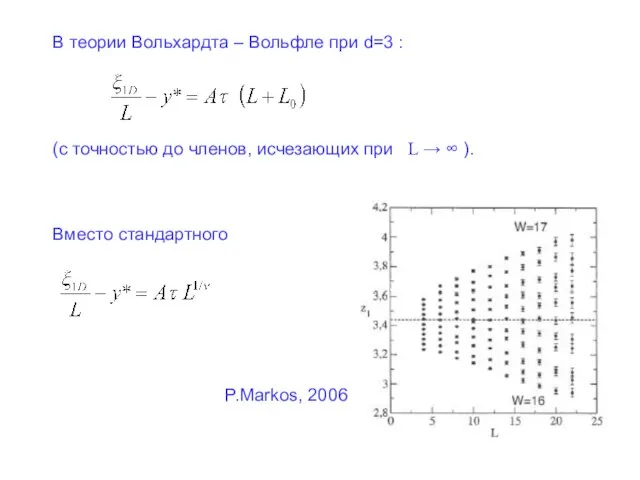
- 26. В теории Вольхардта – Вольфле при d=3 : (с точностью до членов, исчезающих при L →
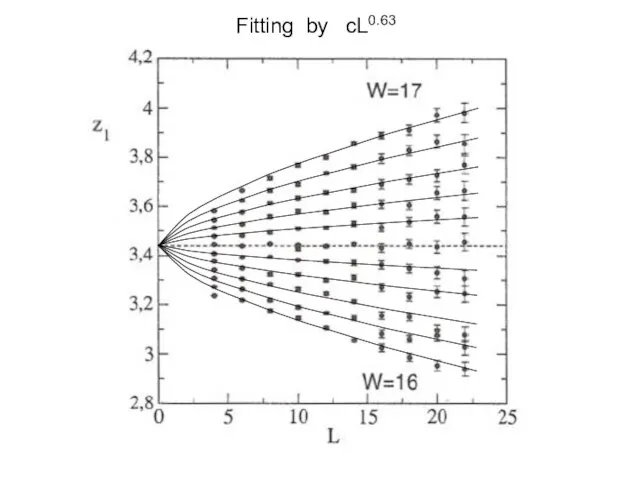
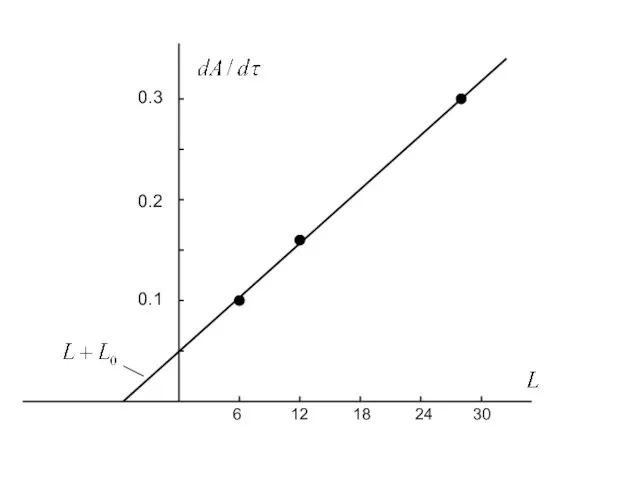
- 27. Fitting by cL0.63
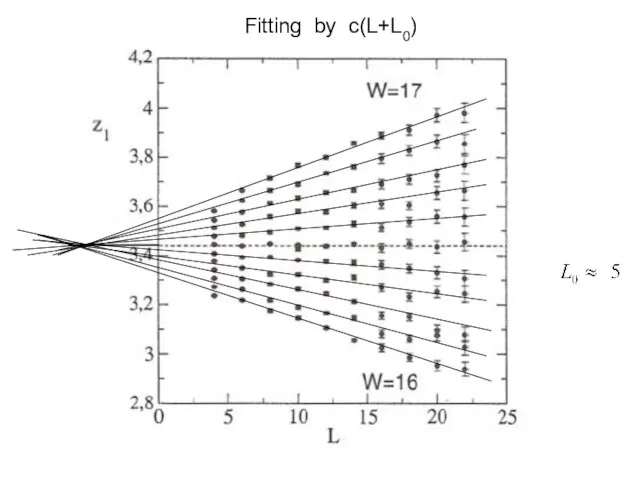
- 28. Fitting by c(L+L0)
- 29. Скейлинг для высших размерностей Меняется ситуация с интегралом Теперь нельзя устремлять Λ → ∞, но зато
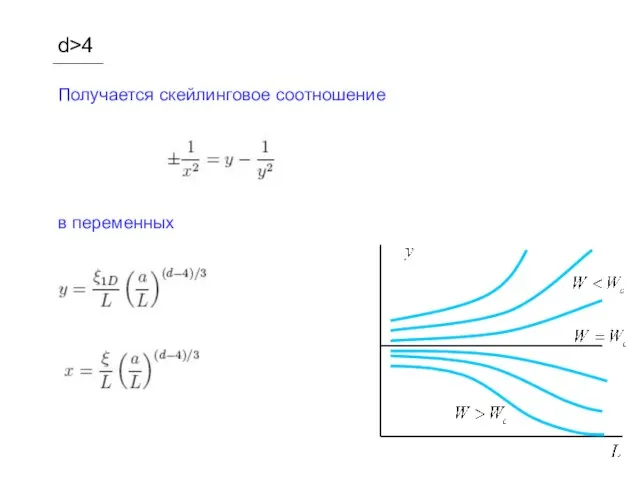
- 30. d>4 Получается скейлинговое соотношение в переменных
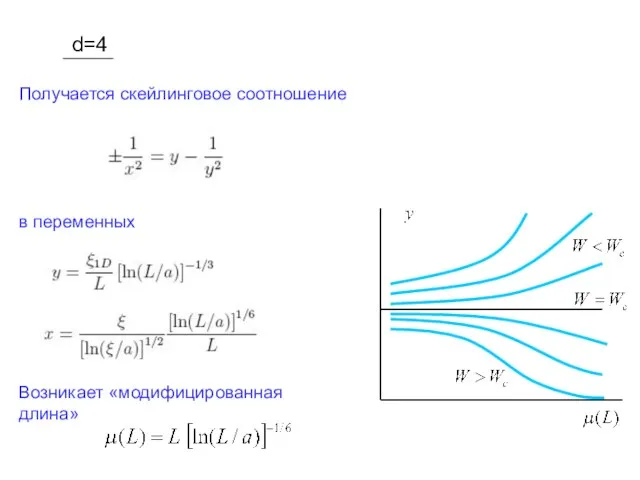
- 31. d=4 Получается скейлинговое соотношение в переменных Возникает «модифицированная длина»
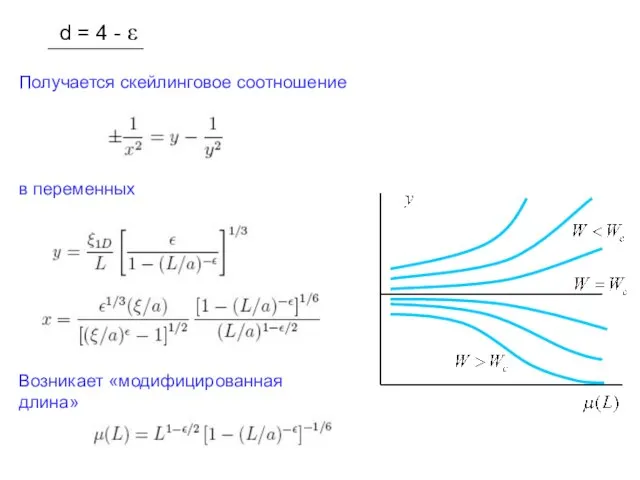
- 32. d = 4 - ε Получается скейлинговое соотношение в переменных Возникает «модифицированная длина»
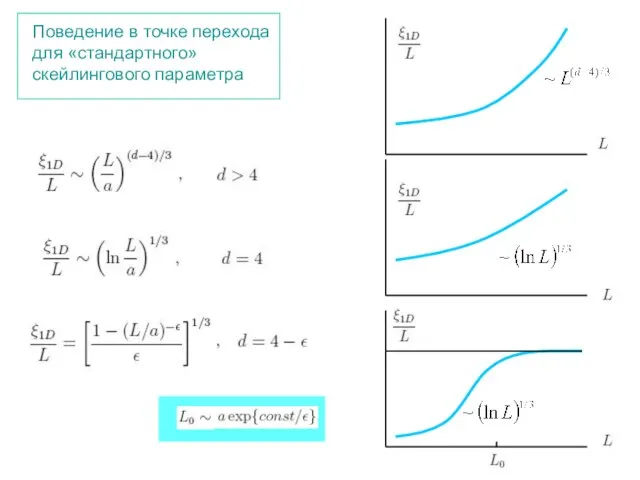
- 33. Поведение в точке перехода для «стандартного» скейлингового параметра
- 34. Другие варианты конечно-размерного скейлинга Квазиодномерные системы Статистика уровней Распределение кондактансов Средний кондактанс Параметр Таулеса («ускорение уровней»)
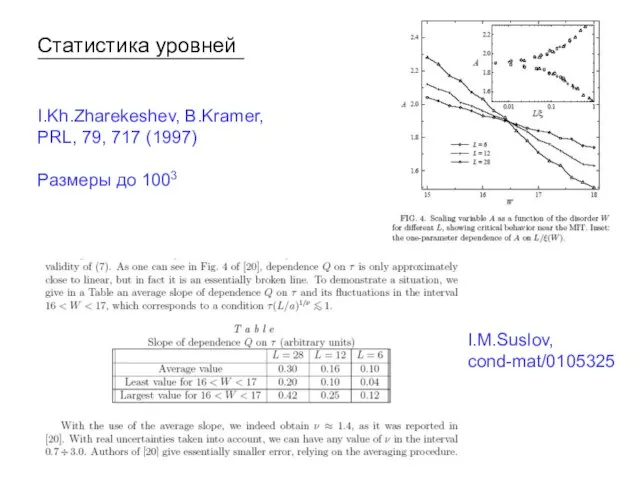
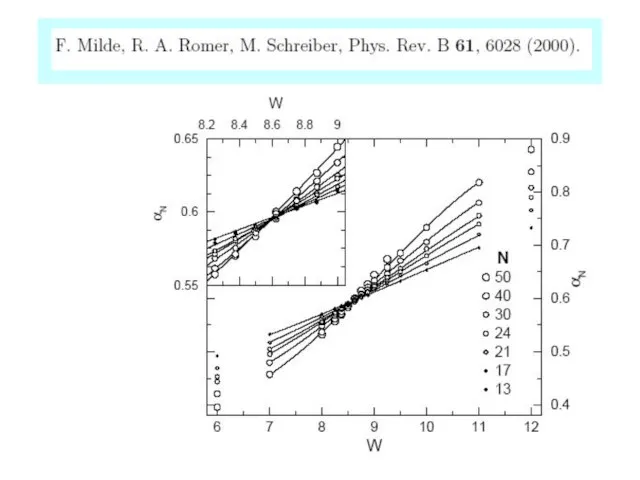
- 35. Статистика уровней I.Kh.Zharekeshev, B.Kramer, PRL, 79, 717 (1997) Размеры до 1003 I.M.Suslov, cond-mat/0105325
- 36. 0.1 0.2 0.3 6 12 18 24 30
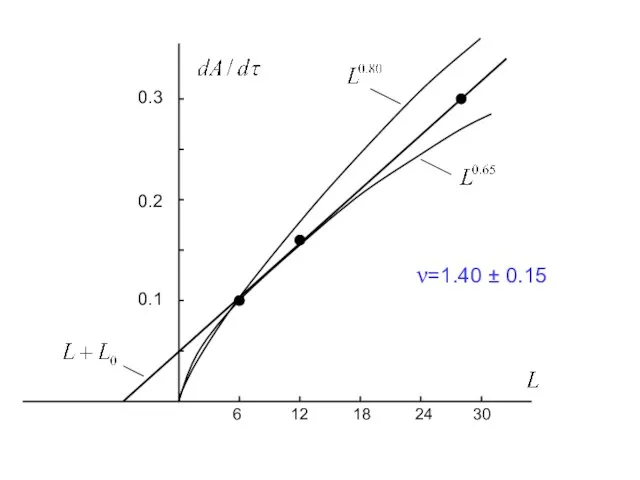
- 37. 0.1 0.2 0.3 6 12 18 24 30 ν=1.40 ± 0.15
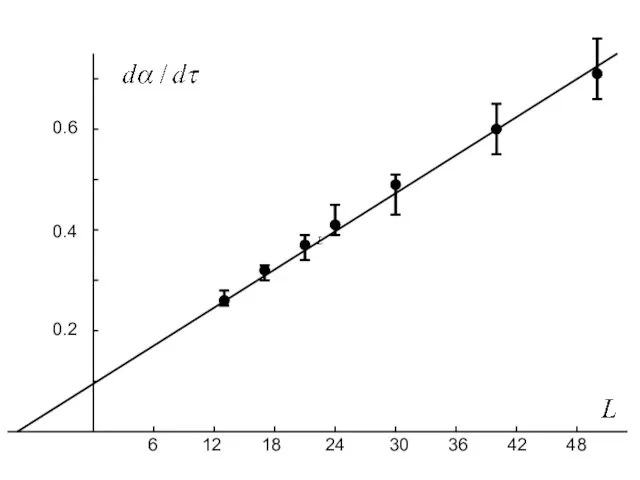
- 39. 0.2 0.4 0.6 6 12 18 24 30 36 42 48
- 41. Скачать презентацию











 Повторение
Повторение Психология ведения группы. Лекция 2
Психология ведения группы. Лекция 2 САХАРНЫЙ ДИАБЕТ СОБАК И КОШЕК
САХАРНЫЙ ДИАБЕТ СОБАК И КОШЕК Публичная защита портфолио как форма представления результатов педагогической деятельности преподавателя школы искусств
Публичная защита портфолио как форма представления результатов педагогической деятельности преподавателя школы искусств Введение вGrid и пакет ‘Глобус’ (Globus Toolkit™)
Введение вGrid и пакет ‘Глобус’ (Globus Toolkit™) Презентация на тему Решение задач 5 класс
Презентация на тему Решение задач 5 класс Жилые модули в Китае
Жилые модули в Китае Художник
Художник Никто не забыт, ничто не забыто
Никто не забыт, ничто не забыто Стекольные работы
Стекольные работы Презентация на тему Рычаг
Презентация на тему Рычаг Проект Здоровый образ жизни
Проект Здоровый образ жизни Докладчик: Заместитель директора СКФОМС Булгакова Татьяна Яковлевна
Докладчик: Заместитель директора СКФОМС Булгакова Татьяна Яковлевна Презентация 10-Э класса
Презентация 10-Э класса Перенашивание беременности
Перенашивание беременности  Животноводствотестокружающий мир3 класс
Животноводствотестокружающий мир3 класс Энергия Солнца
Энергия Солнца Презентация на тему Что можно назвать государством
Презентация на тему Что можно назвать государством 1.Гос политика
1.Гос политика КЛАССА "А"
КЛАССА "А" Исследования как основа проведения информационной кампании
Исследования как основа проведения информационной кампании Обобщенная электрическая машина
Обобщенная электрическая машина Бывалые «охотники» компании «МДМ-Комплект» и рекламное агентство для мебельщиков «РЕКАНА»
Бывалые «охотники» компании «МДМ-Комплект» и рекламное агентство для мебельщиков «РЕКАНА» Презентация на тему Жуки-усачи
Презентация на тему Жуки-усачи Студия «Юный журналист»
Студия «Юный журналист» English is like a global in modern world
English is like a global in modern world Молодежная инициатива.
Молодежная инициатива. 4 модуль_Презентация_проекта_Аутсорсинг производства неметаллов
4 модуль_Презентация_проекта_Аутсорсинг производства неметаллов