Пересечение многогранных поверхностей

Две многогранные поверхности в общем случае пересекаются по пространственной замкнутой ломаной линии
Проницание частичное

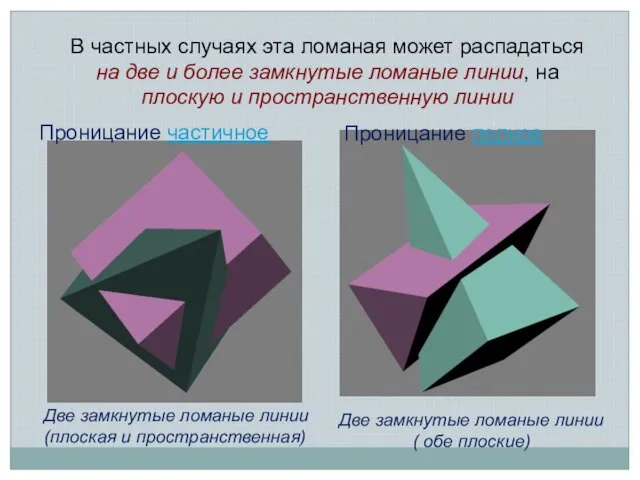
В частных случаях эта ломаная может распадаться на две и более замкнутые ломаные линии, на плоскую и пространственную линии
Проницание полное
Две замкнутые ломаные линии (плоская и пространственная)
Две замкнутые ломаные линии ( обе плоские)
Проницание частичное

Способ ребер − построение вершин ломаной как точек пересечения ребер первого многогранника с гранями второго и ребер второго с гранями первого
Способ граней − построение сторон ломаной как отрезков прямых попарного пересечения граней данных многогранников
прямыми соединяются проекции только тех точек, которые принадлежат одной грани