Пересечение поверхности с плоскостью

Цель и задачи изучения темы
Определить способ заключения прямой линии в плоскость
Выявить характер возможных геометрических фигур при пересечении поверхности и плоскости
Определить способ нахождения натуральной величины фигуры сечения поверхности плоскостью
Лекция 5. Пересечение поверхности с плоскостью

В результате изучения темы Вы будете знать:
Сущность способа заключения прямой линии в плоскость
Способ вспомогательных секущих плоскостей для построения фигур сечения поверхности
Способ преобразования чертежа для определения натуральной величины фигуры сечения
Лекция 5. Пересечение поверхности с плоскостью
В результате изучения темы Вы будете уметь:
Строить проекции сечения поверхности плоскостью
Определять натуральную величину фигуры сечения

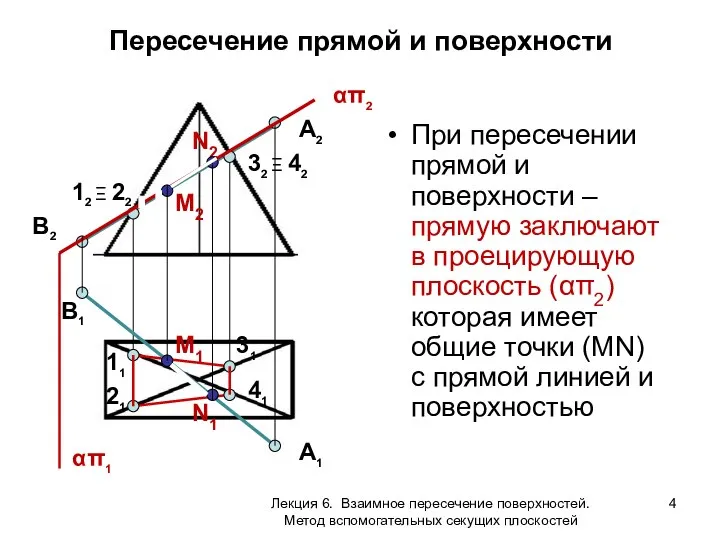
Пересечение прямой и поверхности
При пересечении прямой и поверхности – прямую заключают в проецирующую плоскость (απ2) которая имеет общие точки (MN) с прямой линией и поверхностью
12 Ξ 22
32 Ξ 42
11
21
41
31
Лекция 6. Взаимное пересечение поверхностей. Метод вспомогательных секущих плоскостей
А1
В1
В2
А2
απ2
απ1
M1
M2
N1
N2

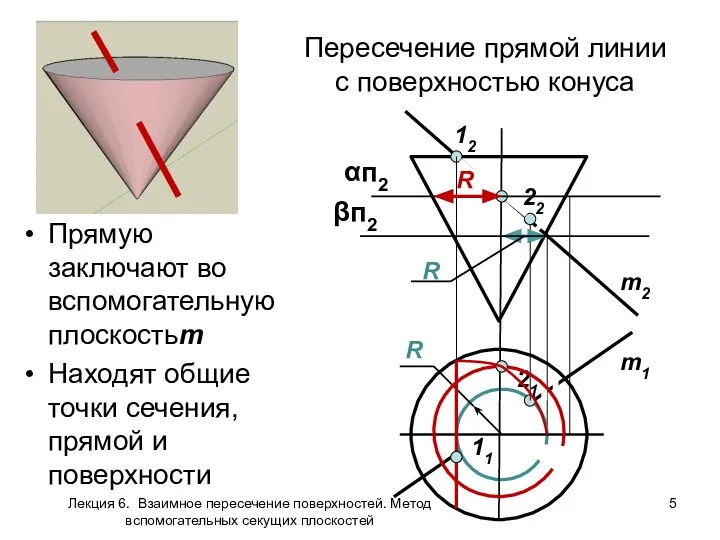
Пересечение прямой линии с поверхностью конуса
Прямую заключают во вспомогательную плоскостьm
Находят общие точки сечения, прямой и поверхности
m2
m1
12
11
22
21
R
R
βп2
Лекция 6. Взаимное пересечение поверхностей. Метод вспомогательных секущих плоскостей
αп2
R

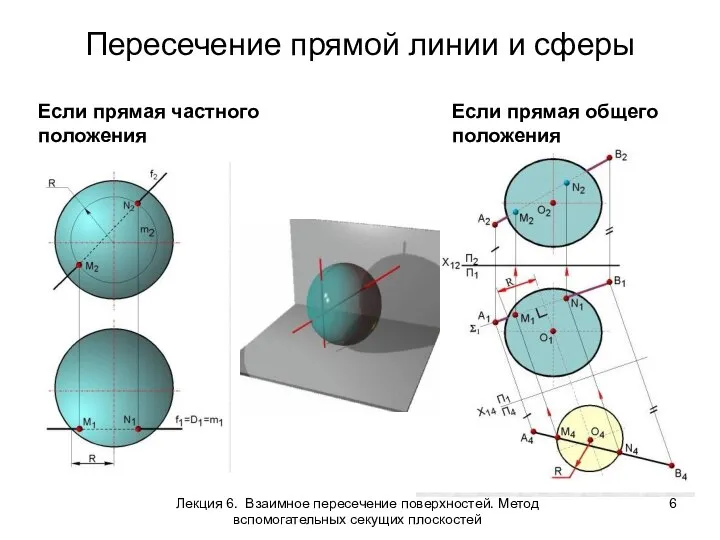
Пересечение прямой линии и сферы
Если прямая частного положения
Если прямая общего положения
Лекция 6. Взаимное пересечение поверхностей. Метод вспомогательных секущих плоскостей

Построение фигуры сечения поверхности плоскостью
Нахождение натуральной величины фигуры сечения
Лекция 6. Взаимное пересечение поверхностей. Метод вспомогательных секущих плоскостей

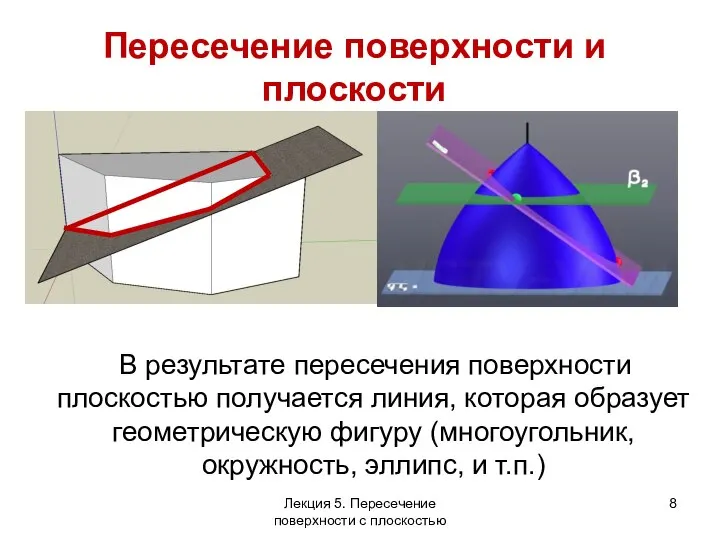
В результате пересечения поверхности плоскостью получается линия, которая образует геометрическую фигуру (многоугольник, окружность, эллипс, и т.п.)
Пересечение поверхности и плоскости
Лекция 5. Пересечение поверхности с плоскостью

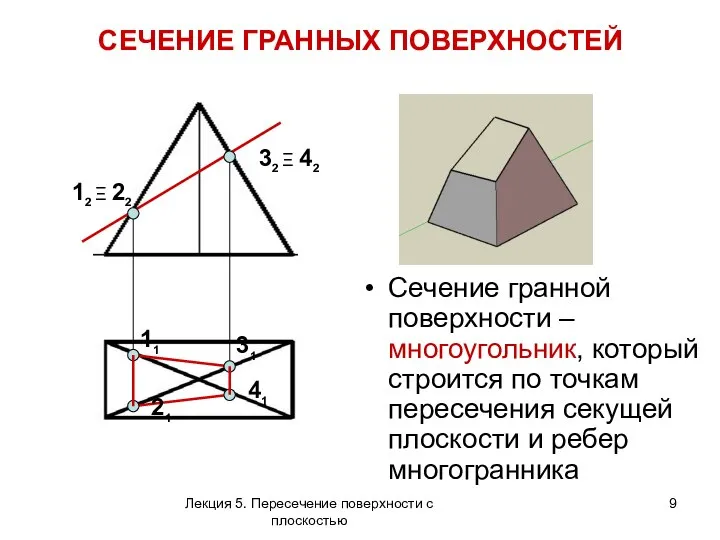
СЕЧЕНИЕ ГРАННЫХ ПОВЕРХНОСТЕЙ
Сечение гранной поверхности – многоугольник, который строится по точкам пересечения секущей плоскости и ребер многогранника
12 Ξ 22
32 Ξ 42
11
21
41
31
Лекция 5. Пересечение поверхности с плоскостью

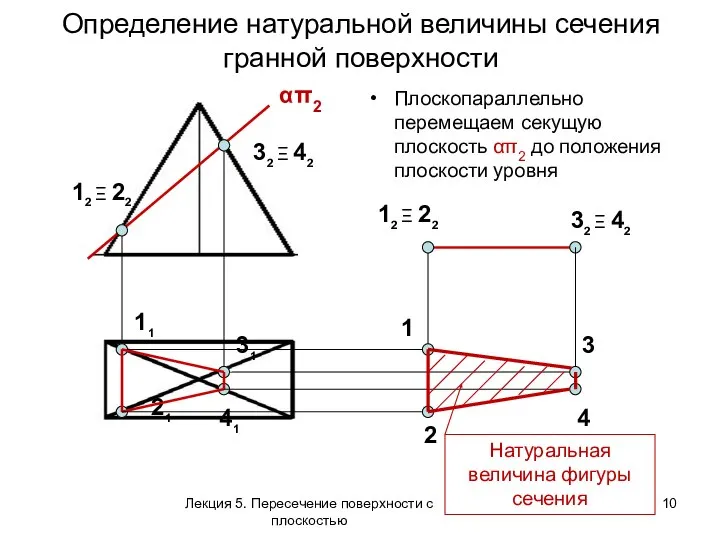
Определение натуральной величины сечения гранной поверхности
12 Ξ 22
32 Ξ 42
11
21
41
31
Лекция 5. Пересечение поверхности с плоскостью
Плоскопараллельно перемещаем секущую плоскость απ2 до положения плоскости уровня
12 Ξ 22
32 Ξ 42
απ2
2
1
3
4
Натуральная величина фигуры сечения

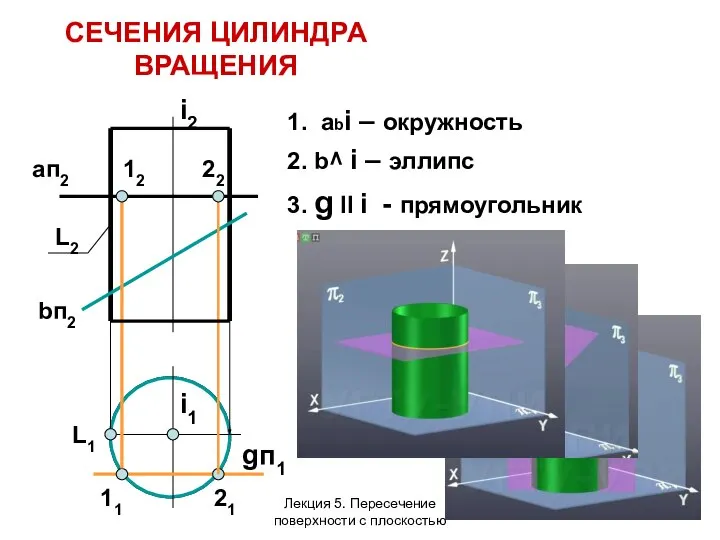
СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ
1. abi – окружность
2. b^ i – эллипс
3. g ll i - прямоугольник
L2
i2
i1
L1
aп2
bп2
gп1
11
21
12
22
Лекция 5. Пересечение поверхности с плоскостью

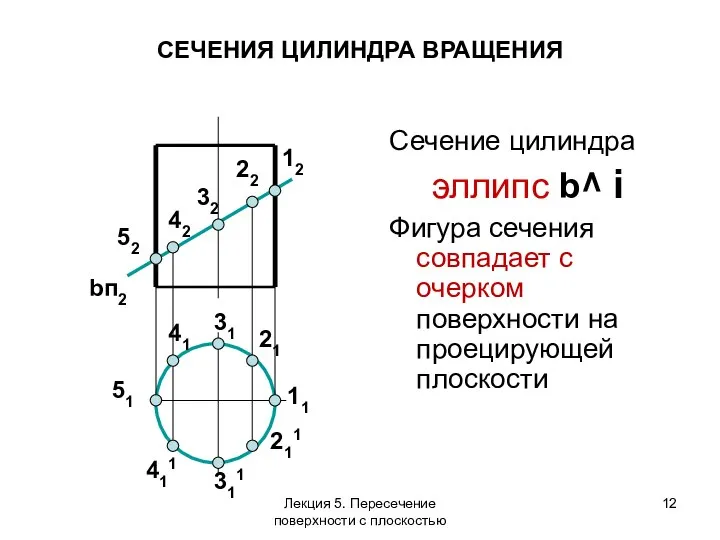
Сечение цилиндра
эллипс b^ i
Фигура сечения совпадает с очерком поверхности на проецирующей плоскости
СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ
12
11
211
21
22
32
31
311
411
42
41
51
52
bп2
Лекция 5. Пересечение поверхности с плоскостью

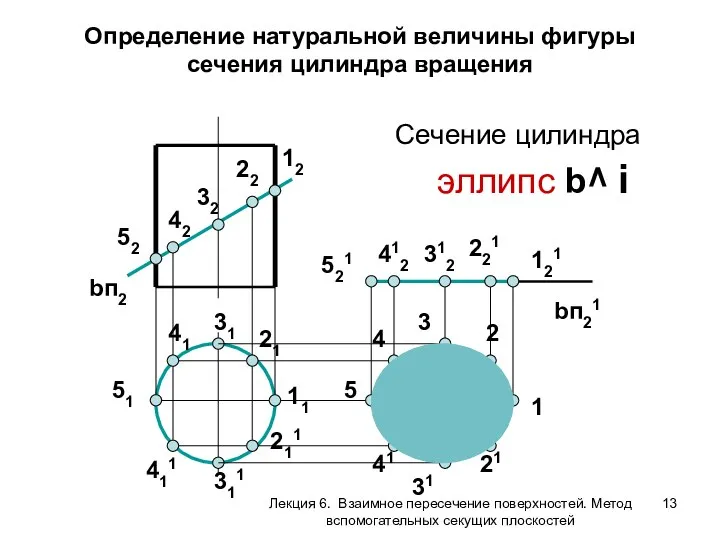
Сечение цилиндра
эллипс b^ i
Определение натуральной величины фигуры сечения цилиндра вращения
bп21
12
121
11
1
2
211
221
21
22
21
32
3
31
311
312
31
411
42
41
412
41
4
51
5
521
52
bп2
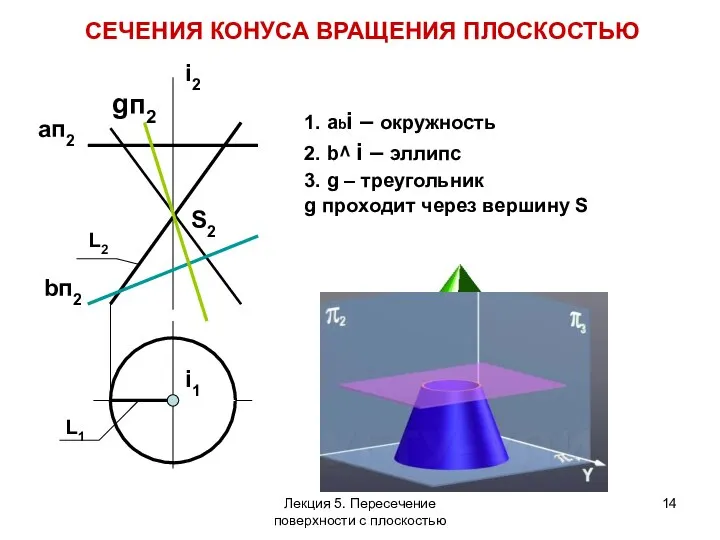
Лекция 6. Взаимное пересечение поверхностей. Метод вспомогательных секущих плоскостей

СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ
1. abi – окружность
2. b^ i – эллипс
3. g – треугольник
g проходит через вершину S
L2
L1
i2
i1
S2
aп2
bп2
gп2
Лекция 5. Пересечение поверхности с плоскостью

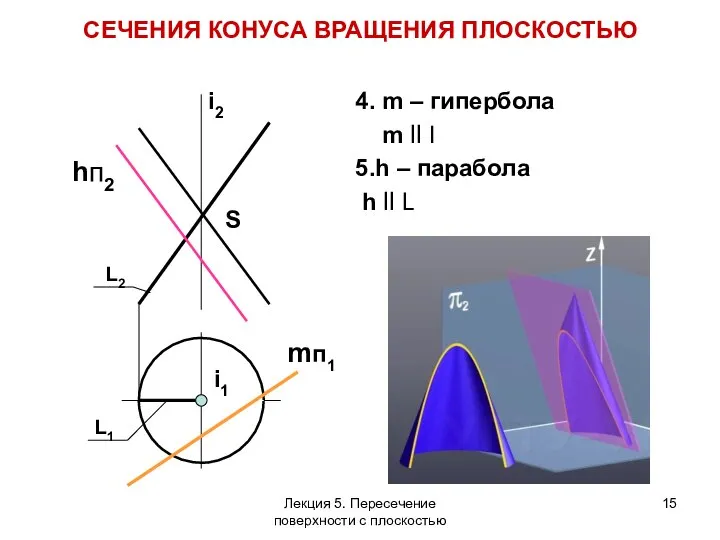
4. m – гипербола
m ll I
5.h – парабола
h ll L
L2
L1
i2
i1
S
СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ
mп1
hп2
Лекция 5. Пересечение поверхности с плоскостью

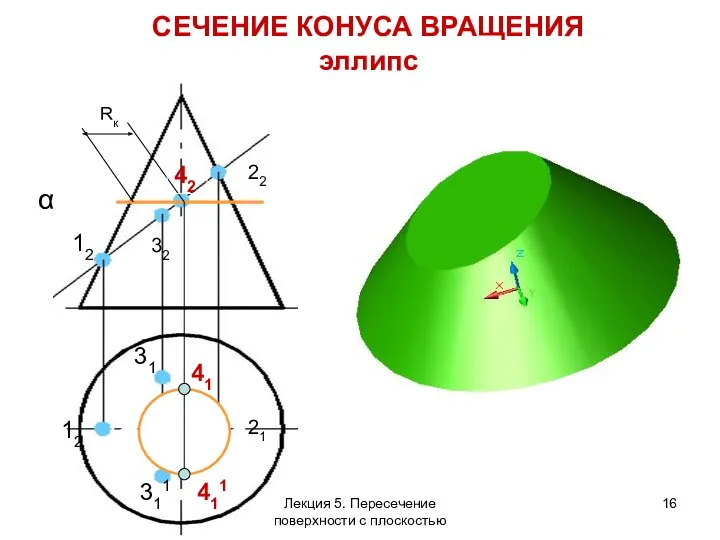
СЕЧЕНИЕ КОНУСА ВРАЩЕНИЯ
эллипс
22
12
32
11
21
αп2
Rк
311
31
Rк
41
411
42
12
311
31
21
12
22
32
Лекция 5. Пересечение поверхности с плоскостью

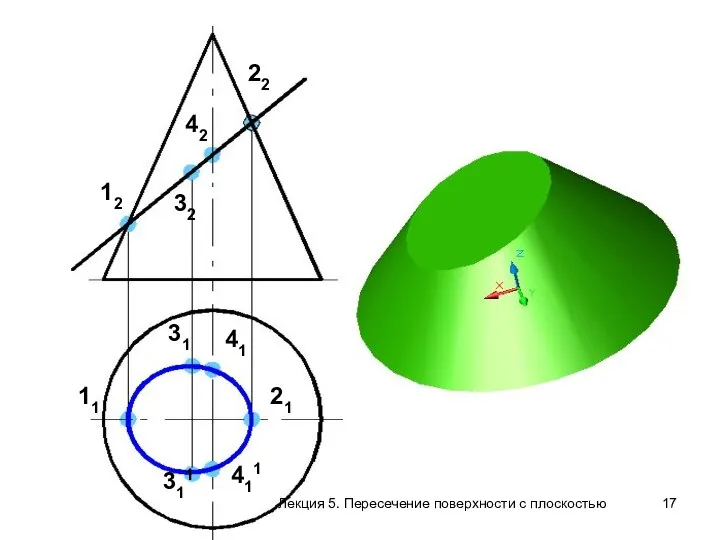
12
11
42
32
22
21
41
411
311
31
Лекция 5. Пересечение поверхности с плоскостью

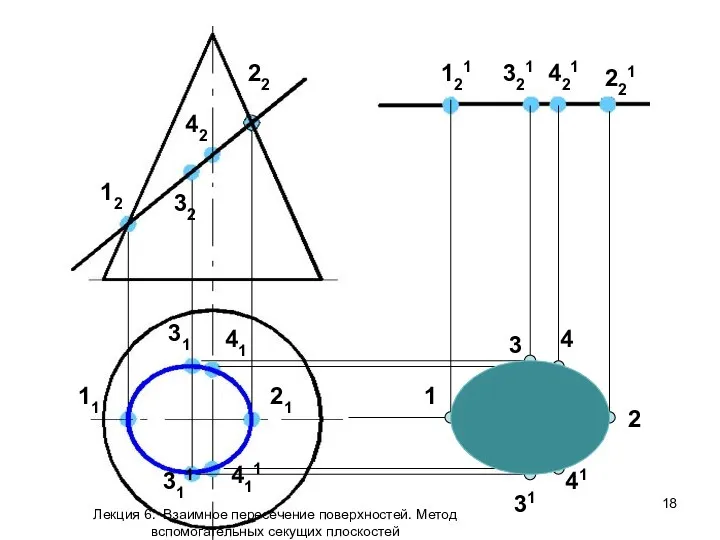
12
11
42
32
22
21
41
411
311
31
121
321
421
221
1
2
31
3
41
4
Лекция 6. Взаимное пересечение поверхностей. Метод вспомогательных секущих плоскостей

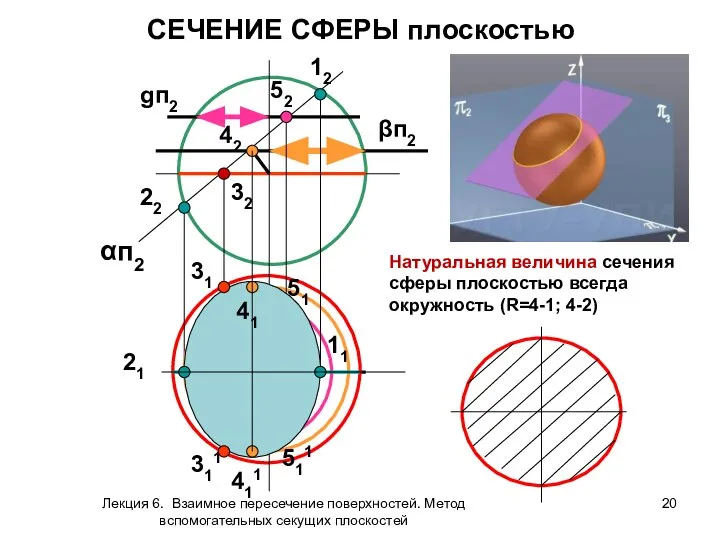
СЕЧЕНИЯ СФЕРЫ
Сечение сферы плоскостью – окружность, которая может проецироваться как:
- прямая линия
- окружность
- эллипс
Лекция 6. Взаимное пересечение поверхностей. Метод вспомогательных секущих плоскостей

СЕЧЕНИЕ СФЕРЫ плоскостью
αп2
12
11
22
21
32
31
311
42
βп2
411
41
gп2
52
51
511
Лекция 6. Взаимное пересечение поверхностей. Метод вспомогательных секущих плоскостей
Натуральная величина сечения сферы плоскостью всегда окружность (R=4-1; 4-2)

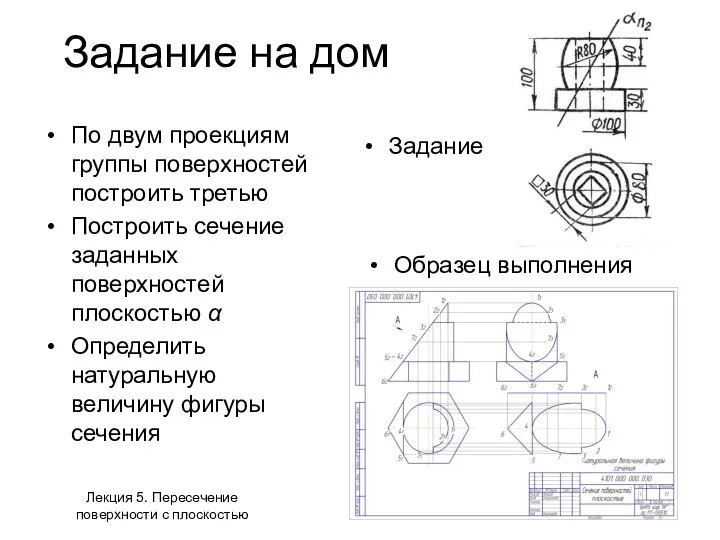
Задание на дом
По двум проекциям группы поверхностей построить третью
Построить сечение заданных поверхностей плоскостью α
Определить натуральную величину фигуры сечения
Задание
Лекция 5. Пересечение поверхности с плоскостью
Образец выполнения

Выводы по теме
Пересечение прямой и поверхности строится методом заключения прямой в дополнительную плоскость
Сечение поверхности плоскостью выполняется с помощью вспомогательной плоскости – посредника
Натуральная величина фигуры сечения строится методом замены плоскостей проекций или плоскопараллельного перемещения
Лекция 5. Пересечение поверхности с плоскостью

Рекомендованная литература
Бударин О. С. Начертательная геометрия. Краткий курс: учеб. пособие для студентов вузов, обучающихся по направлениям в обл. техники и технологий / О. С. Бударин. - 2-е изд., испр. - Санкт-Петербург ; Москва ; Краснодар: Лань, 2009. - 368 с.
Королев Ю. И. Начертательная геометрия: учеб. для вузов инженер.-техн. специальностей / Ю. И. Королев. - 2-е изд. - Москва ; Санкт-Петербург ; Нижний Новгород [и др.]: Питер, 2010. - 256 с.
Чекмарев А. А. Начертательная геометрия и черчение: учеб. для студентов вузов, обучающихся по техн. специальностям / А. А. Чекмарев. - 3-е изд., перераб. и доп. - Москва: Юрайт, 2011. - 471 с.
Лекция 5. Пересечение поверхности с плоскостью