Слайд 2Второй способ перевода
Второй способ – основной – заключается в последовательном делении исходного

десятичного числа на основание той системы, в которую выполняется перевод.
Слайд 3Пример 1
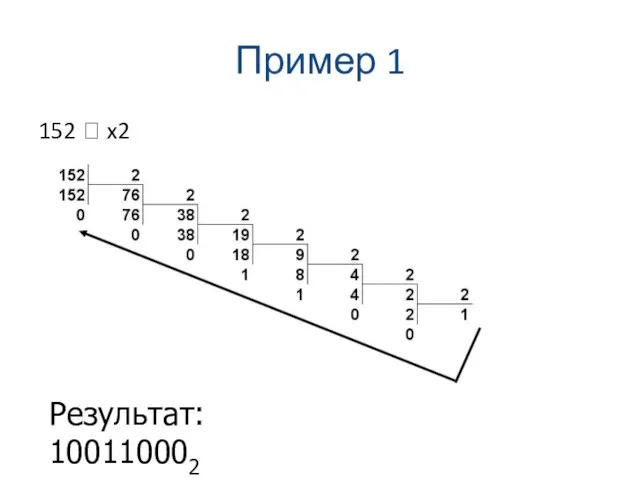
152 ? x2
Результат: 100110002
Слайд 4Пример 2
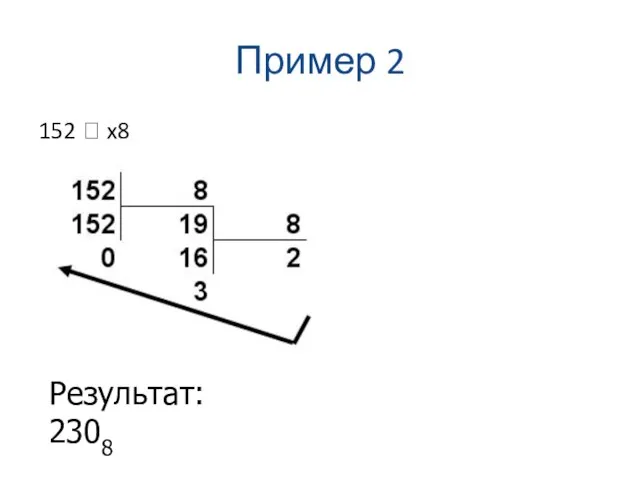
152 ? x8
Результат: 2308
Слайд 5Пример 3
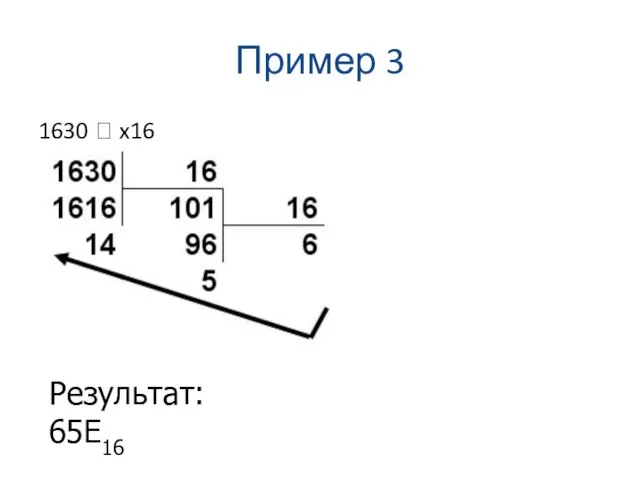
1630 ? x16
Результат: 65E16
Слайд 6Алгоритм действий
Целая часть переводится так, как рассмотрено ранее.
Дробная часть записывается отдельно и

переводится последовательным умножением на основание системы, в которую выполняется перевод с отбрасыванием целой части числа.
Слайд 7Пример 1.
34,75 ? x2
Результат: 34,75 = 100010,112

Слайд 8Пример 2.
0,15 ? x2
Результат: 0,15 = 0,0(1001)2

Слайд 9Пример 3.
0,27 ? x2
Результат: 0,27 ≈ 0,010001010001012

Слайд 10Пример 4.
0,27 ≈ 0,21217270248
0,27 ? x8

Слайд 11Лекция 6
Основы математической логики - 1

Слайд 12Вопросы
Простые и составные высказывания
Логические операции над высказываниями
Свойства логических операций

Слайд 13Высказывания
Под высказыванием будем понимать повествовательное предложение, относительно которого объективно можно сказать, что

оно либо истинно, либо ложно.
Примеры
«Москва – столица Франции», «Корень квадратный из 36 равен 6», «Все лошади имеют по четыре ноги» и т.д. Все эти высказывания объединяет лишь то, что они либо истинны, либо ложны.
Слайд 14Простые и составные высказывания
Высказывания, подобные приведенным выше, называют простыми высказываниями. Они не

могут быть «разложены» на более элементарные высказывания, относительно которых сохранилась бы объективная возможность оценить их истинность.
Из одних высказываний могут составляться (строиться) другие, более сложные высказывания. Такие высказывания мы будем называть составными, или сложными высказываниями.
Слайд 15Построение высказываний
В естественном языке составные высказывания строятся из простых с помощью союзов

(и, или), частицы (не) и словосочетаний (если…, то...; …тогда и только тогда, когда…; …если, и только если…;…необходимо и достаточно для… и т.д.)
Примеры: «Деньги хранят в банке или в коробке из под конфет», «Если все три стороны треугольника равны, то равны и его углы», «Не является верным, что трижды четыре – девять» и так далее.
Слайд 16Условные обозначения
Простые высказывания обозначаются большими буквами начала латинского алфавита: A, B, C

(возможно с индексами: A1, A2, A3 и так далее)
Значения истинности высказываний - буквами И (истина) или 1 и Л (ложь) или 0, которые называют логическими константами.
Слайд 17Логические связки
Связки: союзы (и, или), частица (не) и словосочетания (если…, то...; …тогда

и только тогда, когда…; …если, и только если…;…необходимо и достаточно для… и т.д.)
Соответствующим им операции называют логическими операциями, или логическими связками
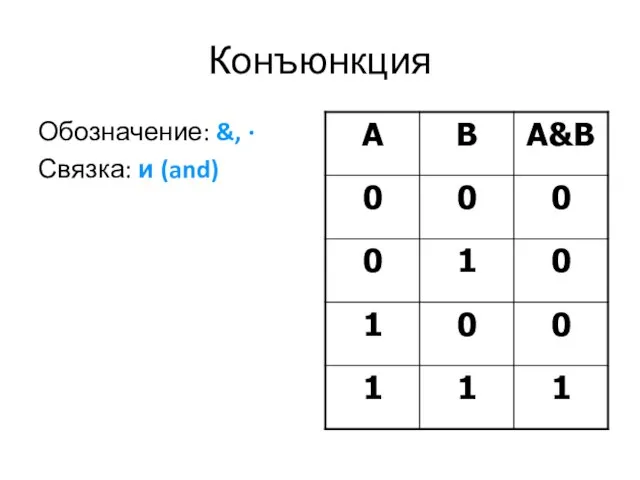
Слайд 18Конъюнкция
Обозначение: &, ∙
Связка: и (and)
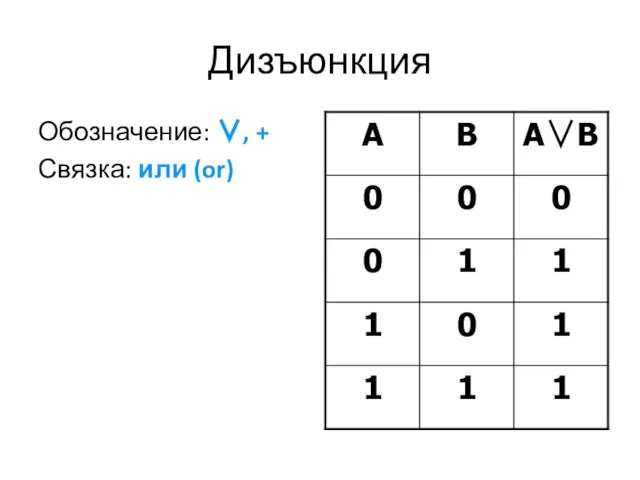
Слайд 19Дизъюнкция
Обозначение: ∨, +
Связка: или (or)
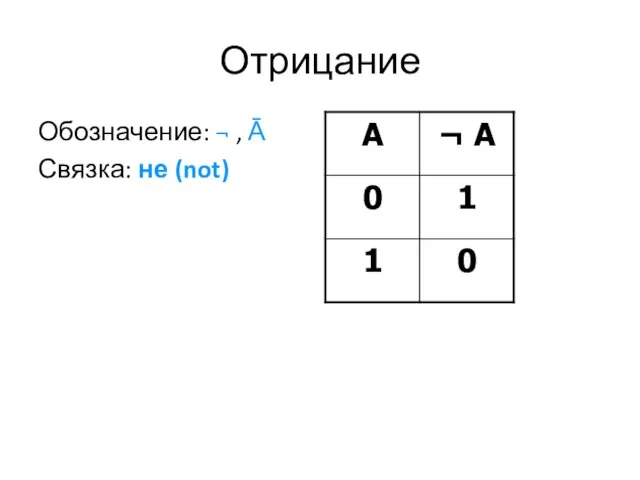
Слайд 20Отрицание
Обозначение: ¬ , Ā
Связка: не (not)
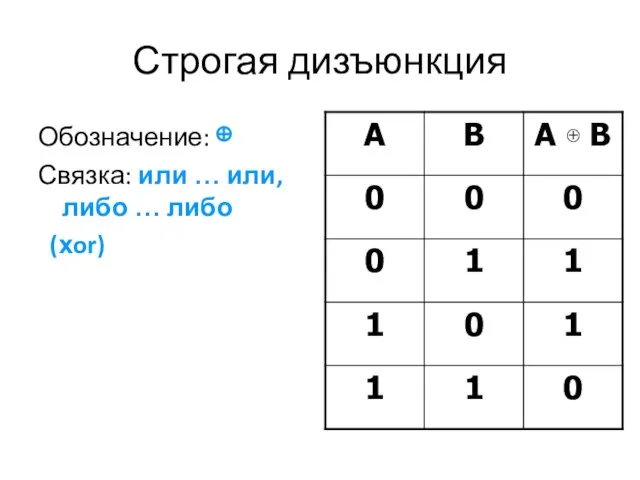
Слайд 21Строгая дизъюнкция
Обозначение: ⊕
Связка: или … или, либо … либо
(хor)
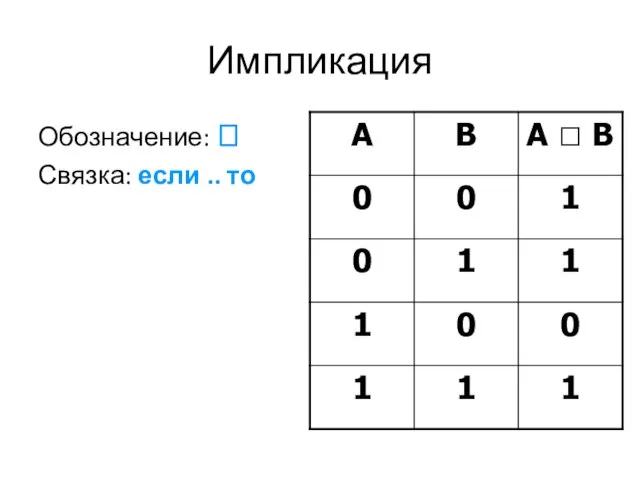
Слайд 22Импликация
Обозначение: ?
Связка: если .. то
Слайд 23Эквиваленция
Обозначение: ~
Связка: ..тогда и только тогда, когда .., ..необходимо и достаточно
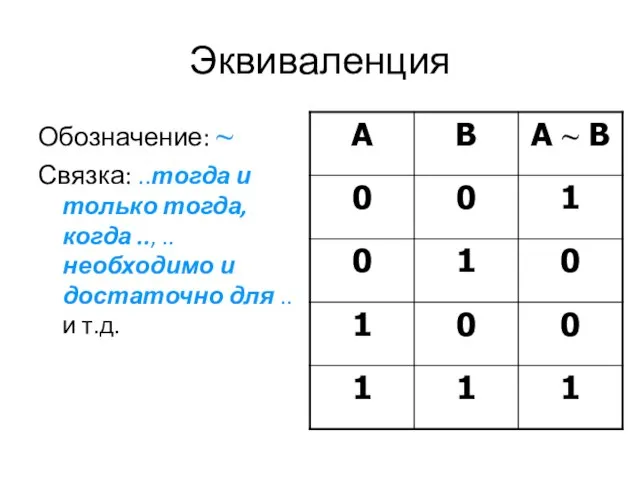
для .. и т.д.
Слайд 24Свойства логических операций
Логическое равенство - утверждение логической равносильности, (логической эквивалентности) двух высказываний.

Логическая равносильность высказываний означает, что значения истинности этих высказываний совпадают. Для обозначения логической равносильности двух высказываний будем использовать символ ≡
Слайд 25Свойства логических операций
Свойства коммутативности
коммутативность конъюнкции: A&B ≡ B&A,
коммутативность дизъюнкции: A∨B

≡ B∨A.
Свойства ассоциативности
ассоциативность конъюнкции:
A&(B&C) ≡ (A&B)&C,
ассоциативность дизъюнкции:
A∨(B∨C) ≡ (A∨B)∨C.
Слайд 26Свойства логических операций
Свойства дистрибутивности
дистрибутивность конъюнкции относительно дизъюнкции:
A&(B∨C) ≡ (A&B) ∨(A&C)

дистрибутивность дизъюнкции относительно конъюнкции:
A∨(B&C) ≡ (A∨B)& (A∨C)
Слайд 27Свойства логических операций
Свойства логических констант
свойства константы И (1):
A&И ≡ A
A∨И ≡ И
свойства

константы Л (0):
A&Л ≡ Л
A∨Л ≡ A
Слайд 28Свойства логических операций
Законы Де Моргана
¬(A&B) ≡ ¬A∨¬B
¬(A∨B) ≡ ¬A&¬B

Слайд 29Свойства логических операций
Закон исключенного третьего
¬A∨A ≡ И
Закон противоречия:
¬A&A ≡ Л
Закон снятия

двойного отрицания:
¬¬A ≡ A




























 Презентация на тему Размножение растений
Презентация на тему Размножение растений  Система Global-ERP Бизнес-приложения для управления предприятием
Система Global-ERP Бизнес-приложения для управления предприятием Избирательное право
Избирательное право ПУЛЬТРУЗИЯПроцессОсновные параметры. FINN ROGER ANDRESENREICHHOLD SANDEFJORD - NORWAY
ПУЛЬТРУЗИЯПроцессОсновные параметры. FINN ROGER ANDRESENREICHHOLD SANDEFJORD - NORWAY Дресс-код ПАО Пермская научно-производственная приборостроительная компания
Дресс-код ПАО Пермская научно-производственная приборостроительная компания Об итогах социально – экономического развития Никифоровского сельского поселения Чусовского муниципального района Пермского кр
Об итогах социально – экономического развития Никифоровского сельского поселения Чусовского муниципального района Пермского кр 7 навыков эффективного лидерства
7 навыков эффективного лидерства «Военного времени дети»
«Военного времени дети» Методы защиты растений от вредителей
Методы защиты растений от вредителей Архитектура абсолютистской Франции
Архитектура абсолютистской Франции Триз (теория решения изобретательских задач)
Триз (теория решения изобретательских задач) Архитектор
Архитектор Контекстная реклама как инструмент повышения продаж
Контекстная реклама как инструмент повышения продаж Презентация на тему ПСОРИАЗ
Презентация на тему ПСОРИАЗ  Consumer buyer behavior
Consumer buyer behavior Презентация на тему:Элементы Комбинаторики!!!
Презентация на тему:Элементы Комбинаторики!!! Познавательная деятельность
Познавательная деятельность Малые архитектурные формы из современных материалов для детских площадок
Малые архитектурные формы из современных материалов для детских площадок The history of our love
The history of our love  Три состояния воды
Три состояния воды Презентация на тему История жевательной резинки
Презентация на тему История жевательной резинки  Direct indirect speech
Direct indirect speech Устное решение квадратного уравнения
Устное решение квадратного уравнения 수정사항 20221007
수정사항 20221007 Микеланджело Буонарроти (1475 - 1564)
Микеланджело Буонарроти (1475 - 1564) Викторина, посвященная Дню Матери. В каких странах, кроме России, празднуется День матери?
Викторина, посвященная Дню Матери. В каких странах, кроме России, празднуется День матери? Требования к условиям реализации образовательных программ начального общего образования
Требования к условиям реализации образовательных программ начального общего образования Регистариция БК на сайте. СуперСамсон - дисконтные и социальные карты
Регистариция БК на сайте. СуперСамсон - дисконтные и социальные карты