Слайд 2лекция №4 Поснтикова Ольга Алексеевна
Контрольные вопросы
Какую случайную величину называют непрерывной?
Что называют плотностью

распределения НСВ?
Как вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу?
Что называют математическим ожиданием НСВ?
Что называют дисперсией НСВ?
Слайд 3лекция №4 Поснтикова Ольга Алексеевна
Контрольные вопросы
(продолжение)
Что называют средним квадратичным отклонением?
Какое распределение вероятностей

НСВ называю нормальным?
Как влияют параметры нормального распределения на форму нормальной кривой?
Как вычислить вероятность попадания в заданный интервал НСВ?
Сформулируйте правило трех сигм и поясните, как его применять на практике
Слайд 4лекция №4 Поснтикова Ольга Алексеевна
План:
1. Плотность распределения и ее свойства.
2. Числовые характеристики

НСВ.
Слайд 5лекция №4 Поснтикова Ольга Алексеевна
1. Плотность распределения и ее свойства
Плотностью распределения

вероятностей или плотностью распределения f (x) непрерывной случайной величины X называется производная ее функции распределения F (x)
Слайд 6лекция №4 Поснтикова Ольга Алексеевна
Ее также называют дифференциальной функцией распределения.

Слайд 7лекция №4 Поснтикова Ольга Алексеевна
Теорема. Вероятность того, что непрерывная случайная величина X

примет значение, принадлежащее интервалу (a ; b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b:
Слайд 8лекция №4 Поснтикова Ольга Алексеевна
2. Числовые характеристики НСВ
Математическим ожиданием непрерывной случайной величины

X, возможные значения которой принадлежат отрезку от a до b, называют определенный интеграл:
Слайд 9лекция №4 Поснтикова Ольга Алексеевна
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата

ее отклонения.
Слайд 10лекция №4 Поснтикова Ольга Алексеевна
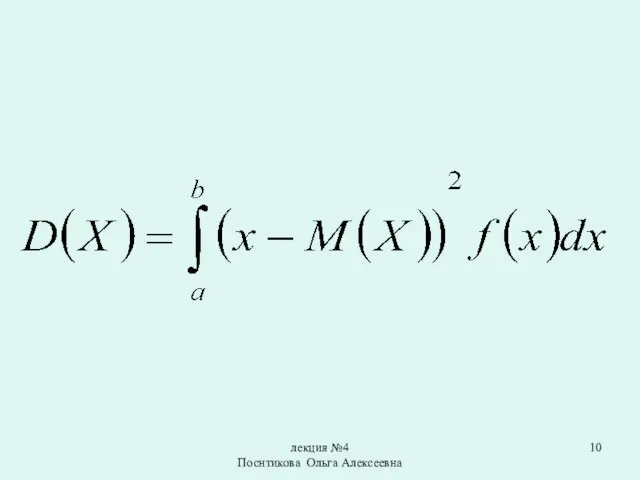
Слайд 11лекция №4 Поснтикова Ольга Алексеевна
Среднее квадратическое отклонение непрерывной случайной величины определяется равенством

Слайд 12лекция №4 Поснтикова Ольга Алексеевна
Замечание 1.
Свойства математического ожидания и дисперсии дискретных

случайных величин сохраняются и для непрерывных величин.
Слайд 13лекция №4 Поснтикова Ольга Алексеевна
Замечание 2.
Для вычисления дисперсии НСВ X можно

использовать формулу:
Слайд 14лекция №4 Поснтикова Ольга Алексеевна
Пример. Найти плотность распределения и числовые характеристики случайной

величины X заданной интегральной функцией распределения
Слайд 15лекция №4 Поснтикова Ольга Алексеевна
Решение.
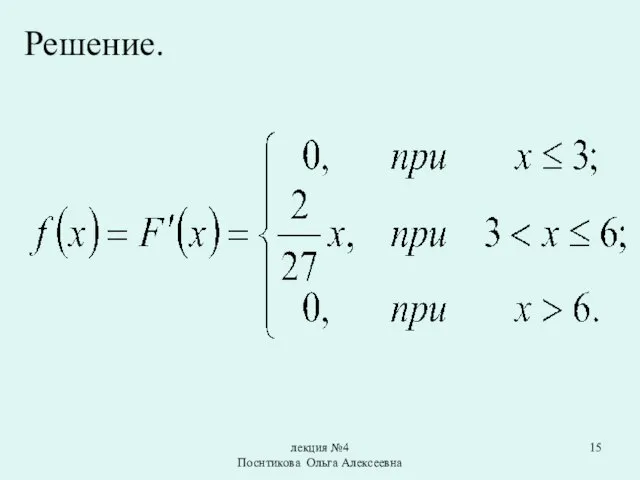
Слайд 16лекция №4 Поснтикова Ольга Алексеевна
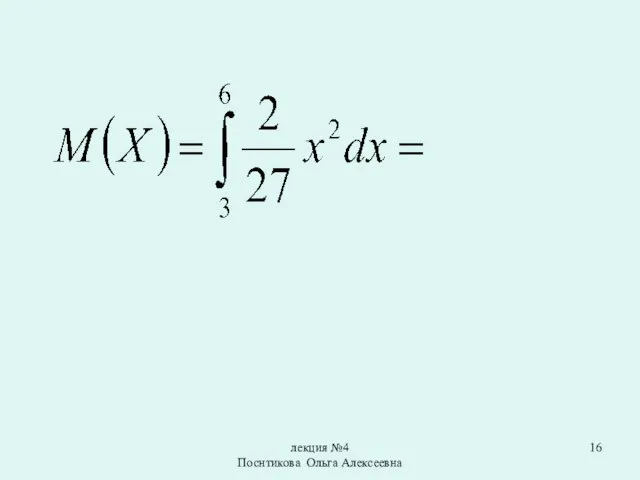
Слайд 17лекция №4 Поснтикова Ольга Алексеевна
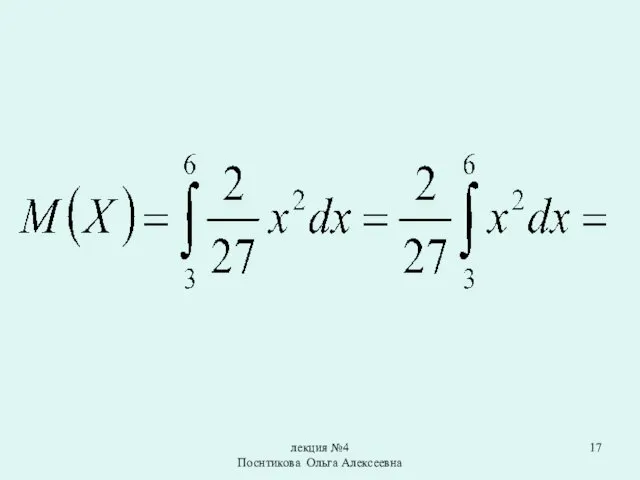
Слайд 18лекция №4 Поснтикова Ольга Алексеевна
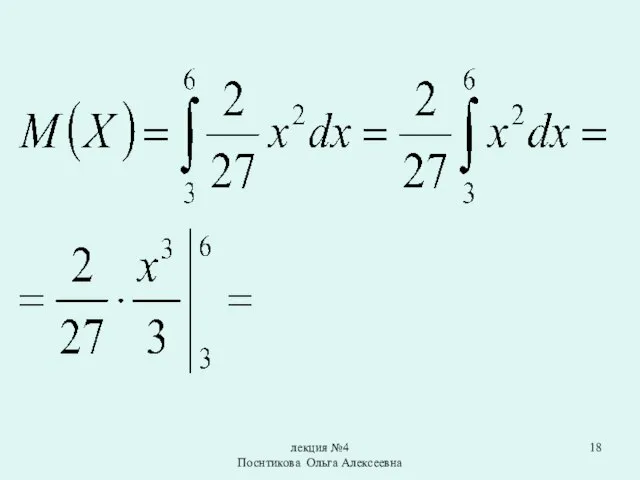
Слайд 19лекция №4 Поснтикова Ольга Алексеевна
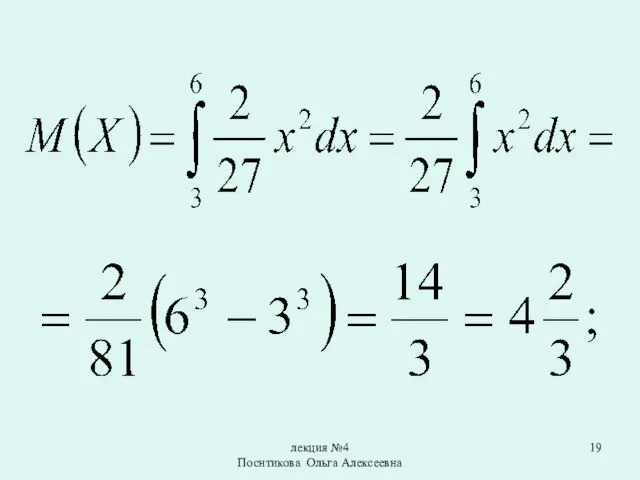
Слайд 20лекция №4 Поснтикова Ольга Алексеевна
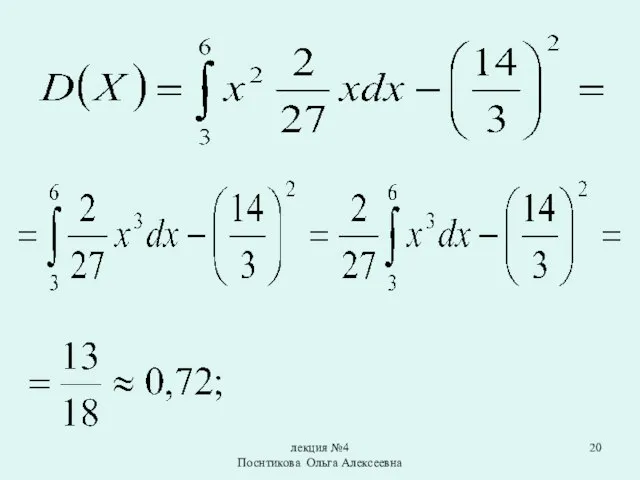








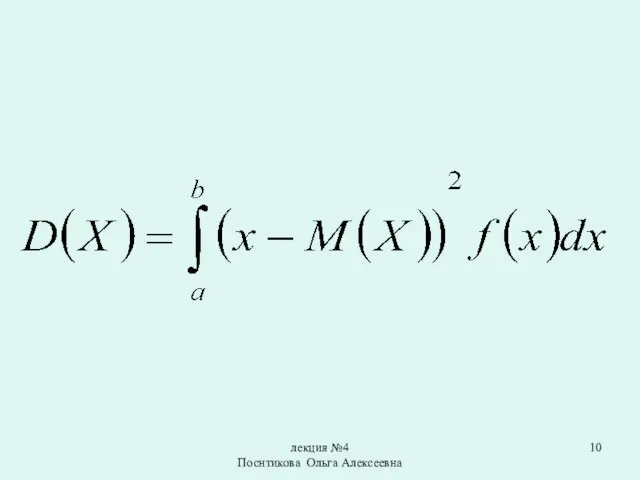




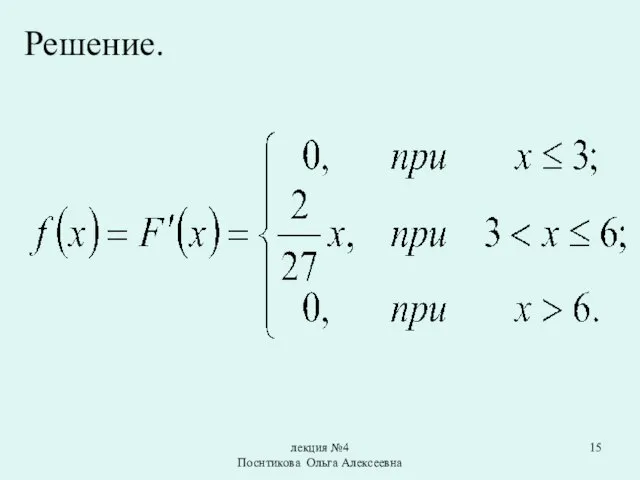
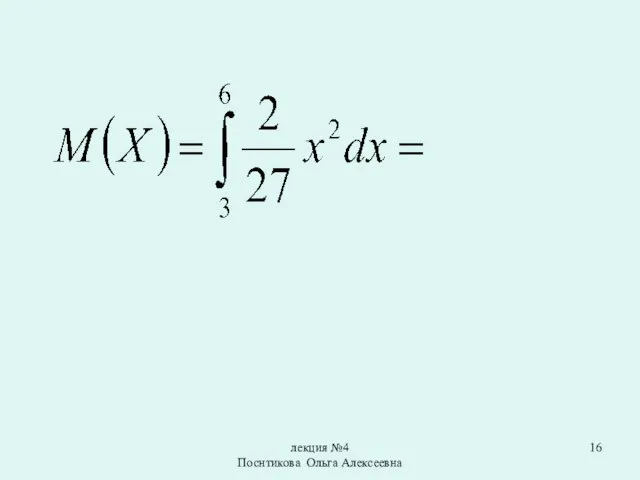
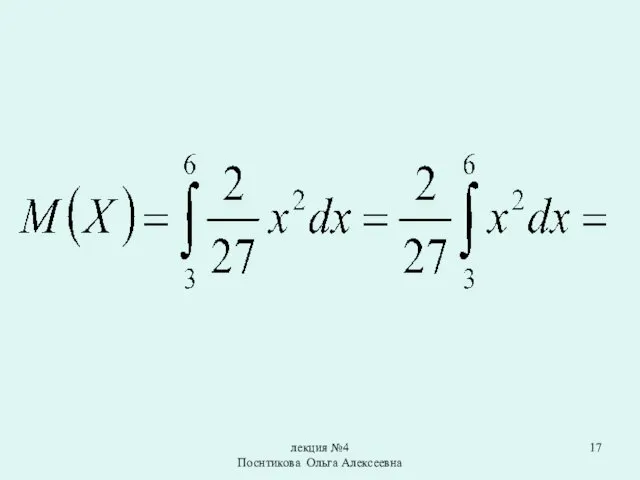
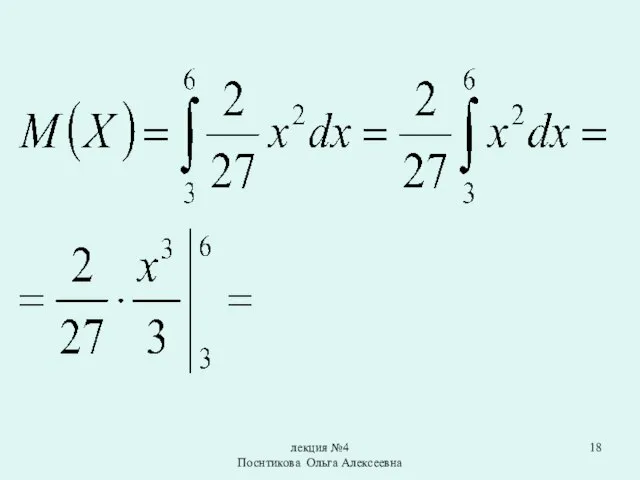
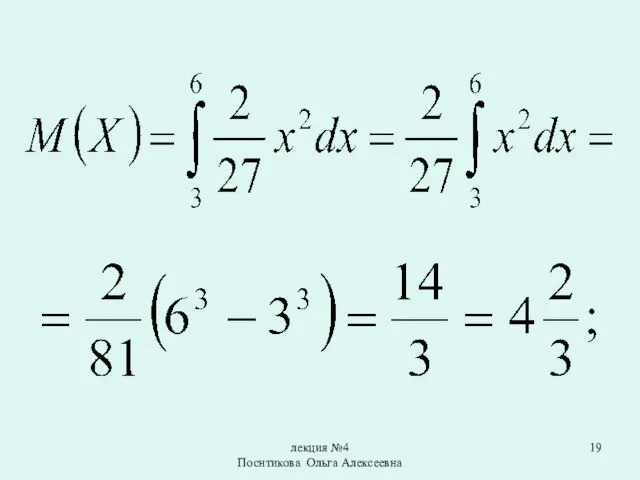
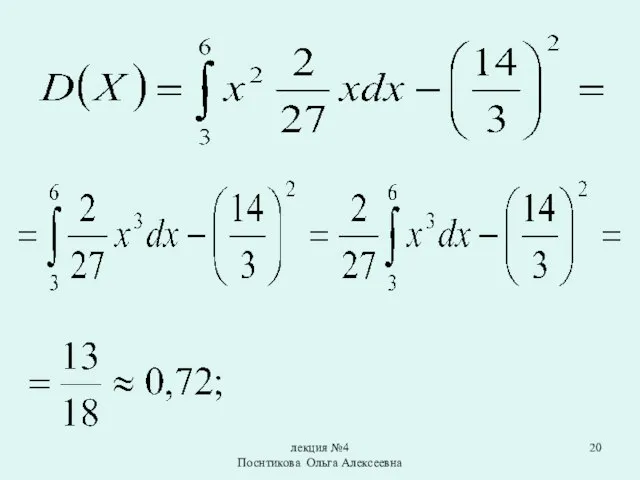
 Владимир Владимир Маяковский
Владимир Владимир Маяковский  Кукольный спектакль Зайкина тётя
Кукольный спектакль Зайкина тётя Презентация на тему Язык HTML
Презентация на тему Язык HTML Культура во второй половине XX-начале XXI века.
Культура во второй половине XX-начале XXI века. Сделай свое лето со 2 июня по 3 августа 2019 года включительно (период действия каталогов №№8–10 2019 года)
Сделай свое лето со 2 июня по 3 августа 2019 года включительно (период действия каталогов №№8–10 2019 года) Презентация на тему: Информация, как основная сущность теории информации
Презентация на тему: Информация, как основная сущность теории информации Тип губки
Тип губки использование религиозных символов в коммерческой рекламе
использование религиозных символов в коммерческой рекламе Prezentatsia1
Prezentatsia1 A real professional. What does it mean?
A real professional. What does it mean? Santa Claus
Santa Claus Внутренняя политика России в начале XXI века – восстановление государства
Внутренняя политика России в начале XXI века – восстановление государства Общественная жизнь России при Николае I
Общественная жизнь России при Николае I Le frasi ridicole
Le frasi ridicole Предложения по подготовке специалистовдля реализации проектов по коммерциализации товаров и услуг ГНСС «ГЛОНАСС»
Предложения по подготовке специалистовдля реализации проектов по коммерциализации товаров и услуг ГНСС «ГЛОНАСС» Создание культурной среды при обучении младших школьников иностранному языку
Создание культурной среды при обучении младших школьников иностранному языку Технические кодексы установившейся практики в области охраны окружающей среды и природопользования
Технические кодексы установившейся практики в области охраны окружающей среды и природопользования Одуванчик
Одуванчик Введение в теорию производства
Введение в теорию производства "ПО ДОРОГАМ ГРАЖДАНСКОЙ ВОЙНЫ"
"ПО ДОРОГАМ ГРАЖДАНСКОЙ ВОЙНЫ" Как фотографировать высокое сооружение
Как фотографировать высокое сооружение Презентация на тему Роль права в жизни государства
Презентация на тему Роль права в жизни государства Презентация на тему Деревья леса
Презентация на тему Деревья леса l_sapr_1-7
l_sapr_1-7 Эффективные способы использования заемных средств, способствующие развитию бизнеса.
Эффективные способы использования заемных средств, способствующие развитию бизнеса. Алиса в стране чудес
Алиса в стране чудес Добровольцы мы (3 раза) В армии Христа. Смело мы идем за своим Вождем, С Ним мы победим врага.
Добровольцы мы (3 раза) В армии Христа. Смело мы идем за своим Вождем, С Ним мы победим врага. Особенности проведенияЕГЭв штатном режиме
Особенности проведенияЕГЭв штатном режиме