Содержание
- 2. Отыскание Унаиб. и Унаим. непрерывной функции у=f(x) на отрезке [a;b] Унаиб= f(b),b –конец отрезка Унаим=f(x1 ),
- 3. Отыскание Унаиб. и Унаим. непрерывной функции у=f(x) на отрезке [a;b] Унаиб= f(а),а –конец отрезка Унаим=f(b ),
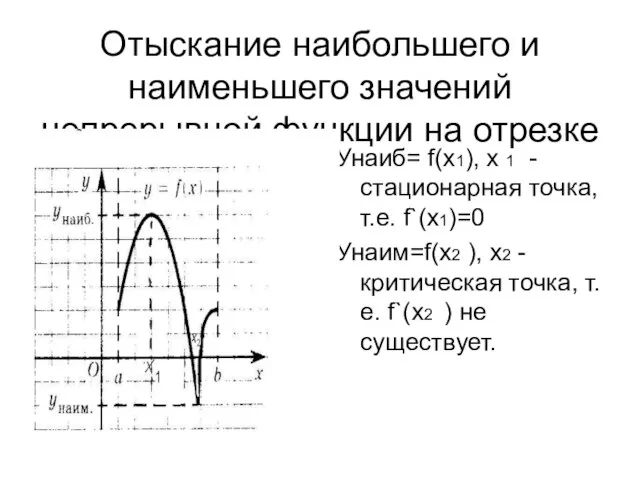
- 4. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке Унаиб= f(x1), х 1 -стационарная точка, т.е.
- 5. Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у=f(x) на отрезке [a;b] 1. Найти производную f`(x)
- 6. Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у=f(x) на отрезке [a;b] 1. Найти производную f`(x)
- 7. I Вариант. Карточка №1 Решение: Д(у)=R 1.у´= 4х-8 (1балл) Д(у´)=R 2. Критических точек нет Стационарные: х=2;
- 8. Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у=f(x) на отрезке [a;b] 1. Найти производную f`(x)
- 10. Скачать презентацию
![Отыскание Унаиб. и Унаим. непрерывной функции у=f(x) на отрезке [a;b] Унаиб= f(b),b](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/394189/slide-1.jpg)
![Отыскание Унаиб. и Унаим. непрерывной функции у=f(x) на отрезке [a;b] Унаиб= f(а),а](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/394189/slide-2.jpg)
![Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у=f(x) на отрезке [a;b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/394189/slide-4.jpg)
![Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у=f(x) на отрезке [a;b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/394189/slide-5.jpg)

![Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у=f(x) на отрезке [a;b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/394189/slide-7.jpg)
 ООО «ЭкоЛайф 69»
ООО «ЭкоЛайф 69» Борьба Руси с иноземным нашествием в XIII в.
Борьба Руси с иноземным нашествием в XIII в. Формы и методы развития исследовательских способностей
Формы и методы развития исследовательских способностей Подбор, обучение и мониторинг персонала Call центров.
Подбор, обучение и мониторинг персонала Call центров. Наследственное право РФ
Наследственное право РФ Приготовление пресного сдобного теста и изделий из него
Приготовление пресного сдобного теста и изделий из него Парковая зона театра им. Натальи Сац
Парковая зона театра им. Натальи Сац правда и вымыслы об акулах
правда и вымыслы об акулах 1. ПР №1 - Тема -1ч. Развитие психики и сознания
1. ПР №1 - Тема -1ч. Развитие психики и сознания Презентация на тему Личные финансы
Презентация на тему Личные финансы Маленькая фея: новинки
Маленькая фея: новинки Настенная живопись
Настенная живопись Комплексное обеспечение процессов в сфере складской логистики, производства и ритейла
Комплексное обеспечение процессов в сфере складской логистики, производства и ритейла Санаторий Марциальные воды в Карелии. Лечение, отдых, встречи
Санаторий Марциальные воды в Карелии. Лечение, отдых, встречи Алгоритм психологической организации группы. Лекция 1
Алгоритм психологической организации группы. Лекция 1 МЕНЕДЖМЕНТ
МЕНЕДЖМЕНТ Современные принципы государственной политики в области МСБ: налоговое регулирование, доступ к финансам
Современные принципы государственной политики в области МСБ: налоговое регулирование, доступ к финансам О финансировании медицинских организаций в системе ОМС в 2011 году и перспективах перехода на одноканальное финансирование в 2011-201
О финансировании медицинских организаций в системе ОМС в 2011 году и перспективах перехода на одноканальное финансирование в 2011-201 Выборы президента школы
Выборы президента школы Оценка информированности учащихся ГБОУ СОШ № 499 по проблемам, связанным с потреблением наркотиков
Оценка информированности учащихся ГБОУ СОШ № 499 по проблемам, связанным с потреблением наркотиков Н.Д. Голев
Н.Д. Голев Продажа маральников и земельных участков
Продажа маральников и земельных участков Автономный контроллер освещения
Автономный контроллер освещения Система управления предприятием Облик-ERP.Конфигурация Оперативное управление предприятием.
Система управления предприятием Облик-ERP.Конфигурация Оперативное управление предприятием. Эмоции эмпатии и вины
Эмоции эмпатии и вины Особенности формирования производственного плана в лесной отрасли
Особенности формирования производственного плана в лесной отрасли Презентация на тему Биологическое действие радиоактивных излучений
Презентация на тему Биологическое действие радиоактивных излучений Школа молодого политика Лидер
Школа молодого политика Лидер