Поговорим о многогранниках

Февраль 7, 2021

Главная
Разное
Поговорим о многогранниках

Содержание

2. Ни одни геометрические тела не обладают таким совершенством и красотой , как правильные многогранники. "Правильных многогранников
4. Правильные многогранники Еще в древней Греции были известны пять удивительных многогранников.
5. Их изучали ученые, ювелиры, священники, архитекторы. Этим многогранникам даже приписывали магические свойства. Древнегреческий ученый и философ
7. Правильные многогранники
8. Тетраэдр Тетраэдр (tetra – четыре, hedra – грань). Правильный тетраэдр – правильный четырехгранник, то есть тетраэдр
9. Гексаэдр Гексаэдр (куб, hexa – шесть). Гексаэдр – правильный многогранник, все грани которого – квадраты, и
10. Октаэдр Октаэдр (okto – восемь). Это правильный многогранник, все грани которого – правильные треугольники и к
11. Додекаэдр Существует правильный многогранник, у которого все грани правильные пятиугольники и из каждой вершины выходит 3
12. Икосаэдр Существует правильный многогранник, у которого все грани – правильные треугольники, и из каждой вершины выходит
13. Полуправильные многогранники
14. Определение: Полуправильным называется выпуклый многогранник, гранями которого являются правильные многоугольники (возможно с разным числом сторон), причем
15. Тела Архимеда
16. Правильная шестиугольная призма Шестиугольная антипризма
17. Усеченный тетраэдр Усеченный икосаэдр Икосододекаэдр Усеченный икосододекаэдр
18. кубооктаэдр усеченный куб плосконосый куб ромбокубооктаэдр
19. Кубооктаэдр Этот полуправильный многогранник получается, если провести в кубе отсекающие плоскости через середины ребер, выходящих из
20. Усеченный куб Если указанным способом срезать вершины куба, то получится полуправильный многогранник, который и называется усеченным
21. ромбоикосододекаэдр плосконосый додекаэдр
22. Звездчатые многогранники
23. Тела Кеплера- Пуансо Кроме правильных и полуправильных многогранников красивые формы имеют так называемые звездчатые многогранники. Правильных
24. Малый звездчатый додекаэдр Большой звездчатый додекаэдр
25. Примечание: Из тетраэдра, куба и октаэдра звездчатые многогранники не получаются. Из додекаэдра получается три. Икосаэдр имеет
26. Это интересно Звездчатые многогранники очень декоративны, что позволяет широко применять их при изготовлении всевозможных украшений. Применяются
28. Скачать презентацию

Слайд 2

Ни одни геометрические тела не обладают таким совершенством и красотой

, как правильные многогранники. "Правильных многогранников вызывающе мало, -написал когда-то Л.Кэролл, - но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук".

Слайд 4

Правильные многогранники

Еще в древней Греции были известны пять
удивительных

многогранников.

Слайд 5

Их изучали ученые, ювелиры, священники, архитекторы. Этим многогранникам даже приписывали магические

свойства. Древнегреческий ученый и философ Платон (IV–V в до н. э.) считал, что эти тела олицетворяют сущность природы. В своем диалоге «Тимей» Платон говорит, что атом огня имеет вид тетраэдра, земли – гексаэдра (куба), воздуха – октаэдра, воды – икосаэдра. В этом соответствии не нашлось места только додекаэдру и Платон предположил существование еще одной, пятой сущности – эфира, атомы которого как раз и имеют форму додекаэдра. Ученики Платона продолжили его дело в изучении перечисленных тел. Поэтому эти многогранники называют платоновыми телами

Слайд 6

Слайд 7

Правильные многогранники

Слайд 8

Тетраэдр

Тетраэдр (tetra – четыре, hedra – грань). Правильный тетраэдр

– правильный четырехгранник, то есть тетраэдр с равными ребрами, представляет собой правильный многогранник, все грани которого – правильные треугольники и из каждой вершины которого выходит ровно три ребра.
Очевидно, что тетраэдр с заданной длиной ребра единственен. Все остальные тетраэдры подобны ему и определяются длиной ребра/

Слайд 9

Гексаэдр

Гексаэдр (куб, hexa – шесть). Гексаэдр – правильный многогранник,

все грани которого – квадраты, и из каждой вершины выходит три ребра.

Слайд 10

Октаэдр

Октаэдр (okto – восемь).
Это правильный многогранник,
все грани

которого – правильные треугольники и к каждой вершине прилегают четыре грани

Слайд 11

Додекаэдр

Существует правильный многогранник, у которого все грани правильные пятиугольники и

из каждой вершины выходит 3 ребра. Этот многогранник имеет 12 граней, 30 ребер и 20 вершин и называется додекаэдром (dodeka – двенадцать).

Додекаэдр Существует правильный многогранник, у которого все грани правильные пятиугольники

Слайд 12

Икосаэдр

Существует правильный многогранник, у которого все грани – правильные треугольники,

и из каждой вершины выходит 5 ребер. Этот многогранник имеет 20 граней, 30 ребер, 12 вершин и называется икосаэдром (icosi – двадцать).

Икосаэдр Существует правильный многогранник, у которого все грани – правильные

Слайд 13

Полуправильные многогранники

Слайд 14

Определение:

Полуправильным называется выпуклый многогранник, гранями которого являются правильные многоугольники (возможно

с разным числом сторон), причем в каждой вершине сходится одинаковое число граней.

Определение: Полуправильным называется выпуклый многогранник, гранями которого являются правильные многоугольники

Слайд 15

Тела Архимеда

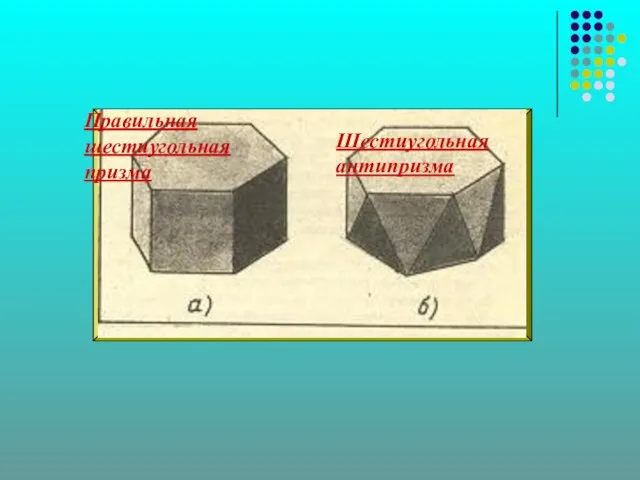
Слайд 16

Правильная шестиугольная призма

Шестиугольная антипризма

Слайд 17

Усеченный тетраэдр

Усеченный икосаэдр

Икосододекаэдр

Усеченный икосододекаэдр

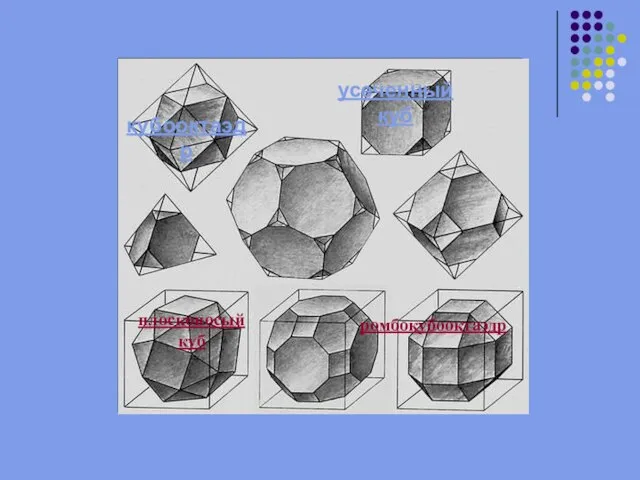
Слайд 18

кубооктаэдр

усеченный куб

плосконосый куб

ромбокубооктаэдр

Слайд 19

Кубооктаэдр

Этот полуправильный многогранник получается, если провести в кубе отсекающие плоскости

через середины ребер, выходящих из одной вершины.
Его гранями являются шесть квадратов, как у куба, и восемь правильных треугольников, как у октаэдра. Отсюда и его название.

Кубооктаэдр Этот полуправильный многогранник получается, если провести в кубе отсекающие

Слайд 20

Усеченный куб

Если указанным способом срезать вершины куба, то получится полуправильный

многогранник, который и называется усеченным кубом

Усеченный куб Если указанным способом срезать вершины куба, то получится

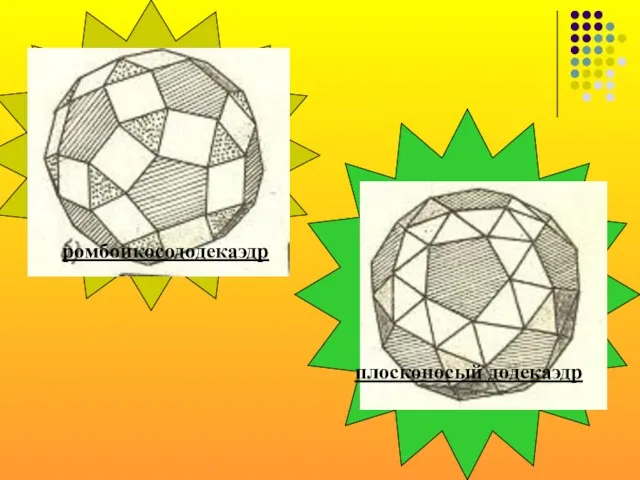
Слайд 21

ромбоикосододекаэдр

плосконосый додекаэдр

Слайд 22

Звездчатые многогранники

Слайд 23

Тела Кеплера- Пуансо

Кроме правильных и полуправильных многогранников красивые формы имеют

так называемые звездчатые многогранники.
Правильных звездчатых многогранников всего четыре. Первые два открыты И. Кеплером, а два других почти 200 лет спустя построил Л. Пуансо.

Тела Кеплера- Пуансо Кроме правильных и полуправильных многогранников красивые формы

Слайд 24

Малый звездчатый додекаэдр

Большой звездчатый додекаэдр

Слайд 25

Примечание:

Из тетраэдра, куба и октаэдра звездчатые многогранники не получаются. Из

додекаэдра получается три. Икосаэдр имеет одну звездчатую форму – большой икосаэдр.

Примечание: Из тетраэдра, куба и октаэдра звездчатые многогранники не получаются.

Слайд 26

Это интересно

Звездчатые многогранники очень декоративны, что позволяет широко применять их при

изготовлении всевозможных украшений. Применяются они и в архитектуре.
Многие формы звездчатых многогранников подсказывает сама природа. Снежинки – это звездчатые многогранники.

Это интересно Звездчатые многогранники очень декоративны, что позволяет широко применять

Поговорим о многогранниках

Содержание

Похожие презентации