Содержание
- 2. «Математика есть прообраз красоты мира». Иоганн Кеплер
- 3. Пифагор 6 век до н.э. Архимед 287-212 гг. до н.э. Евклид 3 век до н.э.
- 4. Многогранники были известны в Древнем Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную
- 5. Правильным многогранником называется многогранник, у которого все грани правильные равные многоугольники, и все двугранные углы равны.
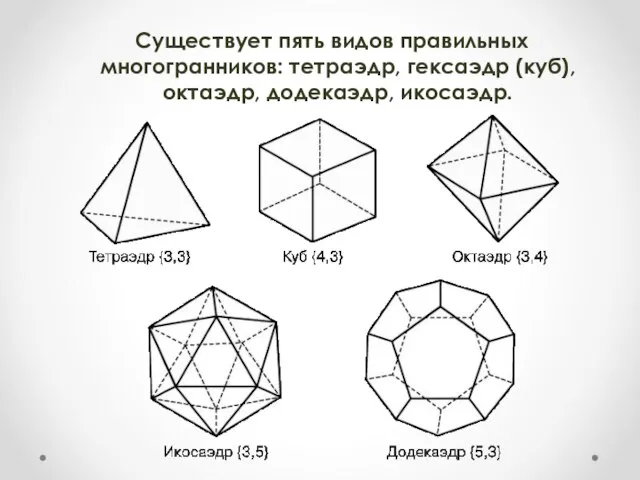
- 6. Существует пять видов правильных многогранников: тетраэдр, гексаэдр (куб), октаэдр, додекаэдр, икосаэдр.
- 7. Эйлер Леонард 1707-1783 гг. Теорема Эйлера о числе граней, вершин и ребер выпуклого многогранника: для любого
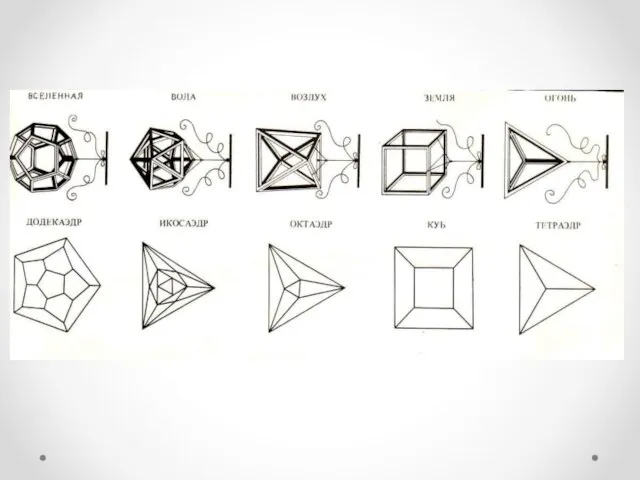
- 8. Пифагорейцы считали правильные многогранники божественными фигурами и использовали в своих философских сочинениях: первоосновам бытия - огню,
- 10. Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий учёный, философ - идеалист
- 11. Правильным многогранникам посвящена последняя, XIII книга знаменитого труда Евклида. Существует версия, что Евклид написал первые 12
- 12. Но есть и такие многогранники, у которых все многогранные углы равны, а грани - правильные, но
- 13. Полуправильные многогранники: усечённый тетраэдр, усечённый октаэдр, усечённый икосаэдр, усечённый куб, усечённый додекаэдр, кубооктаэдр, икосододекаэдр, усечённый кубооктаэдр
- 14. Тела Архимеда
- 15. Кроме полуправильных многогранников из правильных многогранников - Платоновых тел, можно получить так называемые правильные звездчатые многогранники.
- 16. Тела Кеплера - Пуансо. Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр.
- 17. Большой додекаэдр Малый звёздчатый додекаэдр Иоганн Кеплер
- 18. Изображения Леонардо да Винчи додекаэдра методом жестких ребер (а) и методом сплошных граней (б) в книге
- 19. Изображение Леонардо да Винчи усечённого икосаэдра методом жёстких рёбер в книге Л. Пачоли «Божественная пропорция».
- 20. Художественное изображение многогранников в разработанной Леонардо технике жёстких рёбер Титульный лист книги Ж. Кузена «Книга о
- 21. Графические фантазии Маурица Эшера
- 22. Холст, на котором написана "Тайная вечеря" Сальвадора Дали имеет форму золотого прямоугольника. Золотые прямоугольники меньших размеров
- 24. Скачать презентацию



















 Реактивный двигатель ,
Реактивный двигатель , Проблемы и перспективы «дачной амнистии»: взгляд экспертов
Проблемы и перспективы «дачной амнистии»: взгляд экспертов Государство, его признаки и формы
Государство, его признаки и формы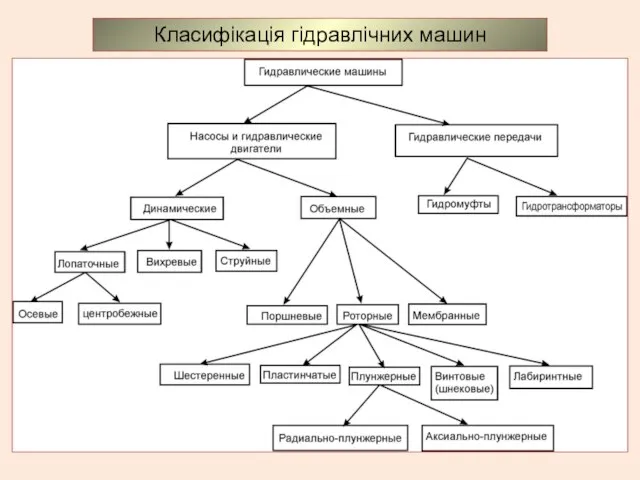 Класифікація гідравлічних машин
Класифікація гідравлічних машин Образы в социальной рекламе
Образы в социальной рекламе Турция
Турция К ВОПРОСУ О РЕГИОНАЛЬНОМ ТЕЛЕМЕДИЦИНСКОМ ЦЕНТРЕСАНКТ-ПЕТЕРБУРГА(ТМЦ СПБ)
К ВОПРОСУ О РЕГИОНАЛЬНОМ ТЕЛЕМЕДИЦИНСКОМ ЦЕНТРЕСАНКТ-ПЕТЕРБУРГА(ТМЦ СПБ) Ежегодно команда юношей принимает участиев межрегиональных соревнованиях среди кадетских корпусов, православных гимназий, дет
Ежегодно команда юношей принимает участиев межрегиональных соревнованиях среди кадетских корпусов, православных гимназий, дет одготовка специалистов для работы с лицами с ОВЗ в Норвегии
одготовка специалистов для работы с лицами с ОВЗ в Норвегии Применение анкерного крепления и хим. упрочнения кровли в условиях Ярегского месторождения
Применение анкерного крепления и хим. упрочнения кровли в условиях Ярегского месторождения Путешествие в город огород
Путешествие в город огород Презентация на тему Духовная жизнь
Презентация на тему Духовная жизнь Питание растений
Питание растений Нормативно-правовые основы и финансово-хозяйственные механизмы перехода на новую систему финансирования
Нормативно-правовые основы и финансово-хозяйственные механизмы перехода на новую систему финансирования Спорт — это здорово
Спорт — это здорово Лев Николаевич Толстой
Лев Николаевич Толстой Prince2 - структурированный метод управления проектами в социальной сфере
Prince2 - структурированный метод управления проектами в социальной сфере Кайнозойская эра
Кайнозойская эра Все профессии важны, с математикой дружны
Все профессии важны, с математикой дружны Физиология, биохимия микроорганизмов (прокариотов: бактерий, эукариотов: простейших, грибов, вирусов)
Физиология, биохимия микроорганизмов (прокариотов: бактерий, эукариотов: простейших, грибов, вирусов) Парад Профессий - ХХI век. Автор Сохибкулова Марина
Парад Профессий - ХХI век. Автор Сохибкулова Марина Trinkgeld für azubis
Trinkgeld für azubis Семинар FCI для судей IGP
Семинар FCI для судей IGP Многогранники
Многогранники Чем интересны музеи
Чем интересны музеи "Пожарные
"Пожарные ОПТИМИЗАЦИЯ ШКОЛЬНОГО САЙТА
ОПТИМИЗАЦИЯ ШКОЛЬНОГО САЙТА к 8 марта с музыкой
к 8 марта с музыкой