Правильная пирамидаподготовила учитель математики Корепанова З.И.

О пирамиде
Термин “пирамида” заимствован
из греческого “пирамис” или “пирамидос”. Греки в свою очередь позаимствовали это слово, как полагают, из египетского языка. В папирусе Ахмеса встречается слово “пирамус” в смысле ребра правильной пирамиды. Другие считают, что термин берет свое начало от форм хлебцев в Древней Греции “пирос” - рожь). В связи с тем, что форма пламени иногда напоминает образ пирамиды, некоторые средневековые ученые считали, что термин происходит от греческого слова “пир” - огонь. Вот почему в некоторых учебниках геометрии XVI в. пирамида названа “огнеформное тело”.

Пирамиду Евклид определяет как телесную фигуру, ограниченную плоскостями, которые от одной плоскости (основания) сходятся в одной точке (вершине). Эго определение подвергалось критике уже в древности, например, Героном,предложившим следующее определение пирамиды: это фигура, ограниченная треугольниками, сходящимися в одной точке, и основанием которой служит многоугольник.

Многогранник, одна из граней которого - многоугольник, а остальные грани - треугольники с общей вершиной, называется пирамидой. Пирамида, основание которой - правильный многоугольник и вершина проектируется в его центр, называется правильной.

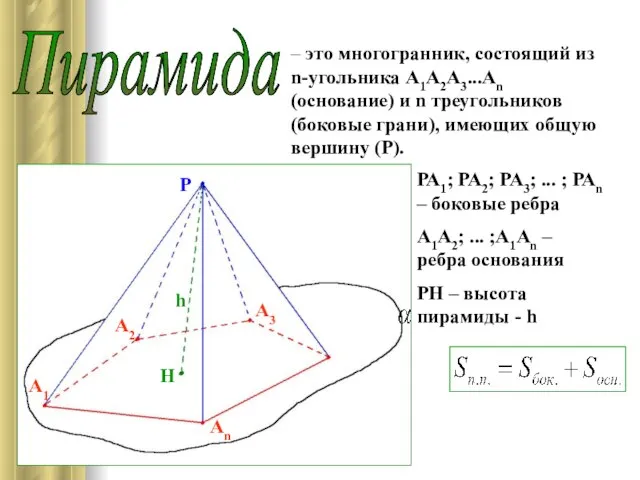
Пирамида
– это многогранник, состоящий из n-угольника А1А2А3...Аn (основание) и n треугольников (боковые грани), имеющих общую вершину (Р).
Р
А1
А2
А3
Аn
H
РА1; РА2; РА3; ... ; РАn – боковые ребра
А1А2; ... ;А1Аn – ребра основания
РH – высота пирамиды - h
h

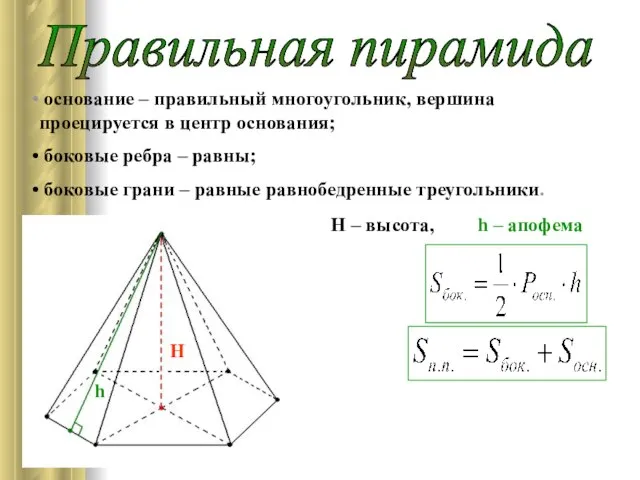
Правильная пирамида
основание – правильный многоугольник, вершина проецируется в центр основания;
боковые ребра – равны;
боковые грани – равные равнобедренные треугольники.
H – высота,
h – апофема
H
h

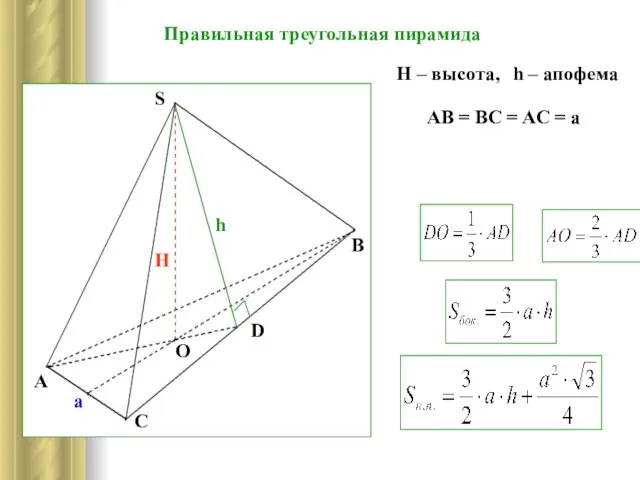
AB = BC = AC = a
Правильная треугольная пирамида
H – высота,
h – апофема
A
O
B
C
h
H
S
D
a

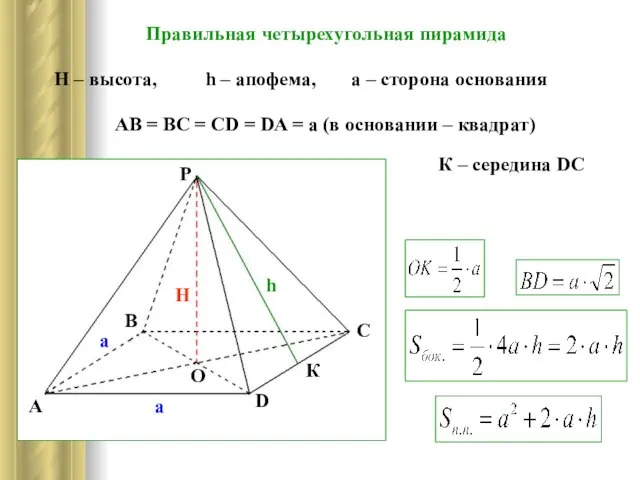
Правильная четырехугольная пирамида
h – апофема,
H – высота,
AB = BC = CD = DA = a (в основании – квадрат)
H
h
a
a
A
B
D
O
P
К
К – середина DC
C
а – сторона основания

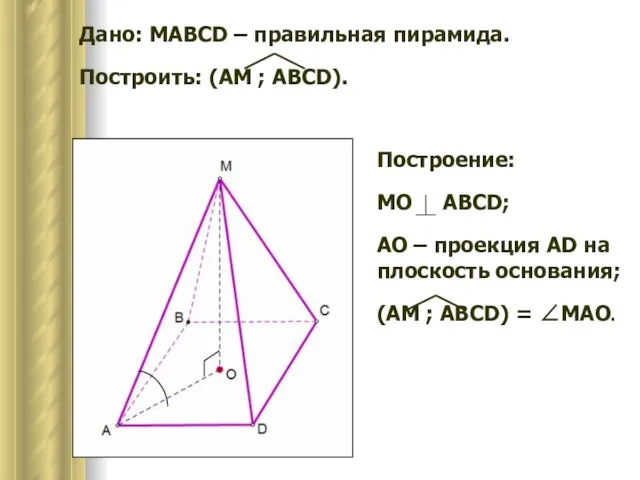
Дано: MAВCD – правильная пирамида.
Построить: (AM ; ABCD).
Построение:
МО ABCD;
AO – проекция AD на плоскость основания;
(AM ; ABCD) = ∠МAO.

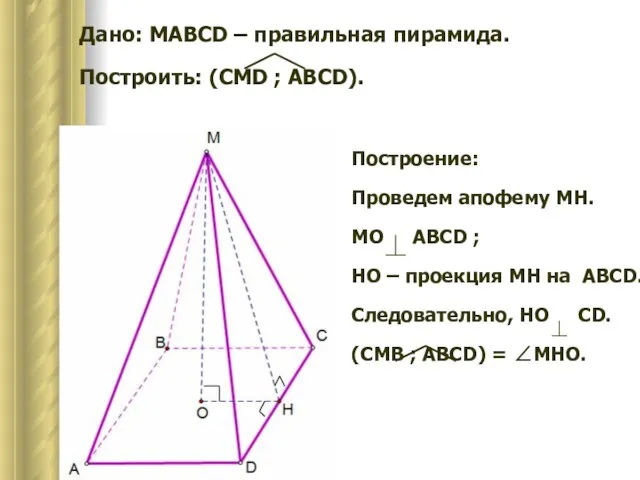
Дано: MAВCD – правильная пирамида.
Построить: (CMD ; ABCD).
Построение:
Проведем апофему МН.
МO AВСD ;
НО – проекция МН на ABCD.
Следовательно, НО CD.
(СMВ ; ABCD) = ∠МНО.

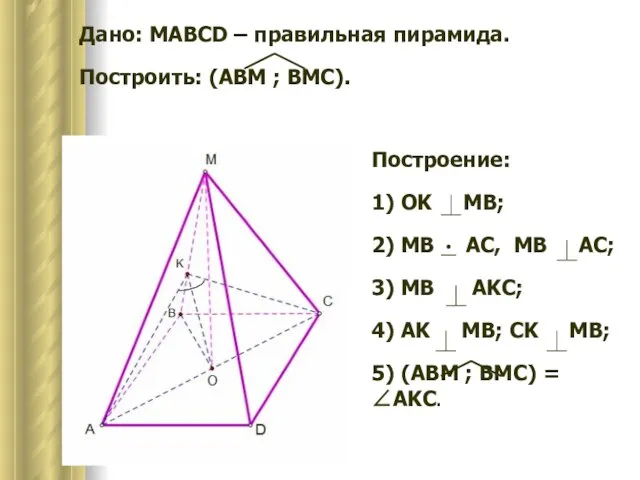
Дано: MAВCD – правильная пирамида.
Построить: (AВM ; BМC).
Построение:
1) OK MB;
2) MB AC, MB AC;
3) MB AKC;
4) AK MB; CK MB;
5) (ABM ; BMC) = ∠AKC.

Примеры пирамид
В природе
В архитектуре
В строительстве

Египетские пирамиды
(по середине пирамида Хеопса высота которой достигает 147м)

На окраине Каира - столицы современного Египта самая высокая - пирамида Хеопса

Центральная Америка к северу от Мехико город Теотиукан
Пирамида Солнца

остров Тенериф: Пирамиды Гуимар

На фоне Гималайского хребта четко выделяется пирамидальное образование – гора Кайлас

Стеклянная пирамида в Париже Новый вход в Лувр, высота 21,65метра