Содержание
- 2. Функция f(x) определена в окрестности точки а (конечной или бесконечной), если а конечная точка, то в
- 3. Определение: Число А называется пределом функции у= f(x) при х стремящимся к хо, если для любого,
- 4. На языке неравенств 2. Односторонние пределы.
- 5. Если область определения функции – множество натуральных чисел N, то аргумент обычно обозначают n. y=f(n), n∈N
- 6. Теорема 1. Теорема « о двух милиционерах» Теорема 2. Если функция f(x) ограничена и монотонна в
- 7. Определения: 1. Функция f(x) называется б.м. в точке а (или при х →а ), если lim
- 8. Теорема 1. (связь между б.м. и б.б. величинами). 1. Если f(x) б.м. в точке а, то
- 9. Итак, ∀ε>0, ∃δ(ε)>0: ∀х∈ Rδ(а) => Отсюда следует, что lim =∞ х →а Вторая часть теоремы
- 10. Теорема 2. Чтобы f(x) при х →а стремилась к конечному пределу А, необходимо и достаточно, чтобы
- 11. Достаточность: Пусть lim ϕ(x) = 0, ϕ(х)=f(x)-А – б.м. в точке а. х → а Это
- 12. 6. Свойства б.м. функций. Теорема 1. Алгебраическая сумма конечного числа б.м. в точке а функций является
- 13. Выберем δ = min (δ1 , δ1 ). Тогда ∀х∈ Rδ(а) оба неравенства будут выполняться одновременно.
- 14. Определение. Функция f(x) называется ограниченной на множестве Х, если существуют такие два числа m и M,
- 15. Теорема 2. Произведение функции f(x), ограниченной в некоторой окрестности точки а на функцию ϕ(x), б.м. в
- 16. Выберем δ = min (δ1 , δ1 ). Тогда ∀х∈ Rδ(а) одновременно |ϕ(x)| | f(x) ⋅
- 17. Замечание. Постоянная функция f(x)= с =const ограничена на всем своем множестве определения. Следствие 2. Произведение двух
- 18. 7.Свойства функций, стремящихся к конечному пределу Теорема 1. Если функция f(x) при х →а стремится к
- 19. Значит (см. теорему 2, параграф 5) f(x)= А+ α (x) f(x)= В+ β (x), где α
- 20. Теорема 2. Если функция f(x) при х →а стремится к конечному пределу, то в некоторой окрестности
- 21. Тогда: m Замечание. В двух последних теоремах точка а может быть как конечной, так и бесконечными
- 22. Джон Непер (1550-1617) – шотландский математик. Изобрел логарифмы: дал определение, объяснение свойств, таблицы и приложения. Рассмотрим
- 23. Положим а=1, в=1/n: f(n)= = = Или f(n)= (*)
- 24. Все скобки в правой части (*) положительны, и все члены в правой части положительны. Перейдем от
- 25. Получим оценку: f(n)= Заменим в знаменателях все множители, большие чем 2, на 2. Правая часть еще
- 26. Сумма n-1 члена: Эта сумма меньше единицы. Получим оценку: f(n)= ∀n∈N
- 27. Функция f(n) возрастает, наименьшее значение принимает при n=1 . f(1)=2 Итак, ∀n∈N: 2≤ f(n) f(n)= -
- 28. Этот предел называют «неперовым числом» и обозначают через «е». е- иррациональное число, выражается бесконечной десятичной дробью
- 29. Число е играет большую роль в математике и в приложениях. Логарифмы при основании е называются натуральными
- 30. Теорема. Если при х→а функции f1(x) и f2(x) стремятся каждая к конечному пределу, то: 1). 2).
- 31. Доказательство единообразно. Докажем вторую часть. По условию , А1 и А2 – числа. Тогда по теореме
- 33. Скачать презентацию





















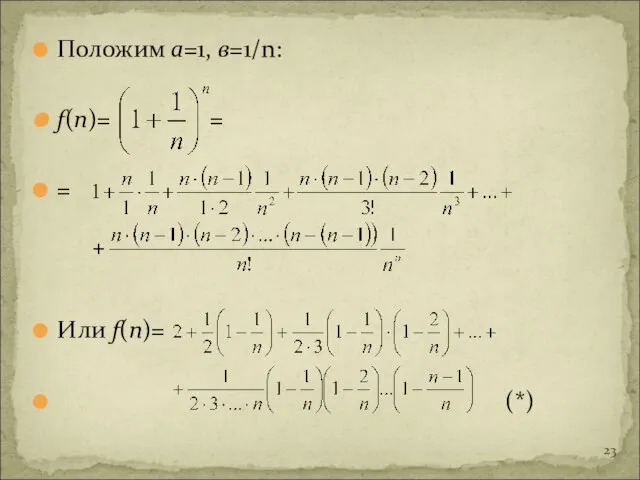








 Кафедра физики
Кафедра физики Грузоперевозки по ДНР и в/из РФ/ЛНР. Прайс
Грузоперевозки по ДНР и в/из РФ/ЛНР. Прайс Аликвота
Аликвота 3-х этажный жилой блок-дом для молодых семей со стенами из блоков
3-х этажный жилой блок-дом для молодых семей со стенами из блоков Эмоциональное реагирование в конфликтах и саморегуляция
Эмоциональное реагирование в конфликтах и саморегуляция Уважаемые Дамы и Господа! Холдинг «Западно-Европейский Финансовый Союз» - динамично развивающаяся группа компаний, предоставляющ
Уважаемые Дамы и Господа! Холдинг «Западно-Европейский Финансовый Союз» - динамично развивающаяся группа компаний, предоставляющ Безопасность при пожаре
Безопасность при пожаре К.Г. Паустовский Кот-ворюга
К.Г. Паустовский Кот-ворюга Презентация на тему Декарт и Спиноза: обоснование рационализма
Презентация на тему Декарт и Спиноза: обоснование рационализма  Понятие о профессии, специальности и квалификации работника. Классификация профессий
Понятие о профессии, специальности и квалификации работника. Классификация профессий 21.12.2015
21.12.2015 Секреты правильного питания
Секреты правильного питания Переводы Библии
Переводы Библии Деловая игра «Строим дом».
Деловая игра «Строим дом». Jobs and occupations
Jobs and occupations Частные Ростовские типографии XIX –начала XX вв.
Частные Ростовские типографии XIX –начала XX вв. Мы развиваем Ваши сильные качества
Мы развиваем Ваши сильные качества Учет поступления и расхода товара в аптеке
Учет поступления и расхода товара в аптеке Краткая история иконописи на Руси
Краткая история иконописи на Руси Почему в темноте человек не может идти прямо
Почему в темноте человек не может идти прямо Чудесный мир насекомых
Чудесный мир насекомых Человек Божий - Даниил
Человек Божий - Даниил Услуги АО Федеральная корпорация по развитию малого и среднего предпринимательства
Услуги АО Федеральная корпорация по развитию малого и среднего предпринимательства Долгий путь бутерброда…или гигиена питания
Долгий путь бутерброда…или гигиена питания Сочинение на лингвистическую тему(СЛТ)
Сочинение на лингвистическую тему(СЛТ) РЕБУСЫ
РЕБУСЫ Лидогенерация – как основной инструмент маркетинговой деятельности и развития бизнеса
Лидогенерация – как основной инструмент маркетинговой деятельности и развития бизнеса Лидогенерация
Лидогенерация