Представленние чисел в компьютере

Позиционная система счисления
Целое число x в b-ричной системе счисления представляется в виде конечной линейной комбинации степеней числа b
Важные системы счисления
двоичная, восьмеричная и шестнадцатеричная

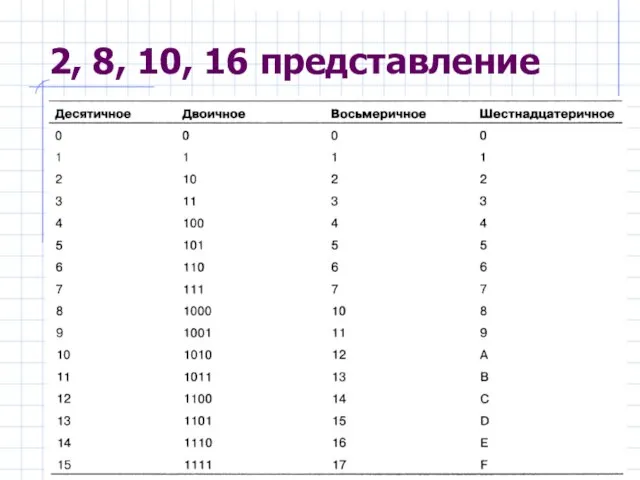
2, 8, 10, 16 представление

Число 2001

Правила
2
1 + 1 = 10
8
7 +1 = 10
16
F + 1 = 10
1A9F
3AB
1
+
(1) F + B = F + 1 + A = 10 + A = 1A
(2) 1 + 9 + A = A + A = 14
(3) 1 + A + 3 = E
1
A
4
E
1

Преобразование чисел из одной системы счисления в другую
Перевод произвольной позиционной системы счисления в десятичную
Например

Перевод из десятичной в произвольную позиционную систему счисления
Целая часть
1. Последовательно делить целую часть десятичного числа на основание, пока десятичное число не станет равно нулю.
2. Полученные при делении остатки являются цифрами нужного числа. Число в новой системе записывают, начиная с последнего остатка.

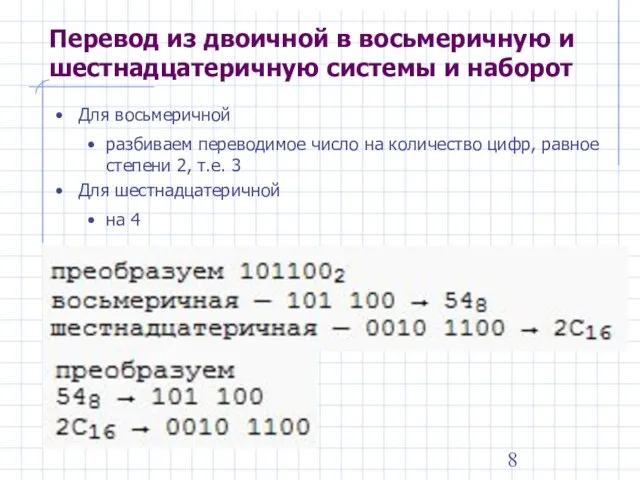
Перевод из двоичной в восьмеричную и шестнадцатеричную системы и наборот
Для восьмеричной
разбиваем переводимое число на количество цифр, равное степени 2, т.е. 3
Для шестнадцатеричной
на 4

Отрицательные двоичные числа
Существует несколько систем
Рассмотрим дополнение до двух
Х + (-Х) = 0
Правило преобразования в отрицательное число
Сначала каждая единица меняется на ноль, а каждый ноль — на единицу
Затем к полученному результату прибавляется единица
Число +6:
00000110 ? 11111001
-6: 11111010
Проверка:
00000110 + 11111010 = 0

Числа с плавающей точкой
Дробное число хранится в форме мантиссы и показателя степени
Стандарт IEEE 754
Реализация математических операций с числами с плавающей запятой в вычислительных системах может быть как аппаратная, так и программная

IEEE 754
Определения форматов хранения мантиссы, экспоненты и знака, форматы положительного и отрицательного нуля, плюс и минус бесконечностей, а также определение "не числа" (NaN).
Методы, которые будут использоваться для округления числа в процессе математических операций.
Обработка исключительных ситуаций, таких как деление на ноль, переполнение и т.д.

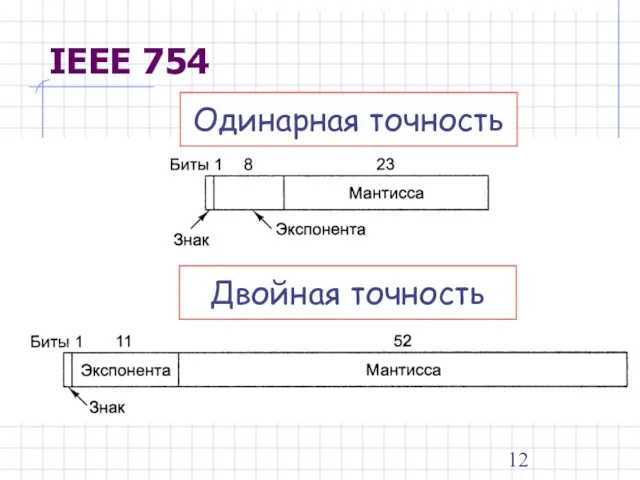
IEEE 754
Одинарная точность
Двойная точность

IEEE 754

IEEE 754 - типы

Преобразование из IEEE 754
Экспонента
011111002 = 12410
Мантисса
01000000000000000000000
Для вычисления показателя степени из восьмиразрядного поля экспоненты вычитается смещение экспоненты равное 12710
011111002 - 011111112 = 12410 - 12710 = -310

Преобразование из IEEE 754
Для вычисления мантиссы к единице добавляется дробная часть мантиссы из 23-х разрядного поля дробной части мантиссы 1,01000000000000000000002.
Число равно произведению мантиссы со знаком на двойку в степени экспоненты
1,012*2-3 = 1012*2-5 = 5*2-5 = 0,15625
1,012*2-3 = (1 + 0*2-1 + 1*2-2) * 2-3 = 2-3 + 2-5 = 0,15625

Преобразование в IEEE 754
13 = 1101 = 1.101 * 2^3
Экспонента
3 + 127 = 130 = 10000010
Мантисса
10100000000000000000000
Число 13 в IEEE 754
0.10000010.10100000000000000000000

Преобразование в IEEE 754
155.625
1*27 +0*26+0*25+1*24+1*23+0*22+1* 21+
1*20+1*2-1+0*2-2+1*2-3
128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 + 0.5 + 0 + 0.125
155.625 = 10011011.101 - число в двоичной системе с плавающей точкой

Преобразование в IEEE 754
155.625
10011011.101 =1.0011011101*2+7 =
= 1.0011011101*2+111
число в нормализованном экспоненциальном виде
смещенная экспонента
7 + 127 = 134 = 100001102
710 = 1112
1 бит
0
8 бит
10000110
23 бит
00110111010000000000000

Примеры - Python
>>> a = 2**1000
>>> a
10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376L
>>> x = 0.1
>>> x
0.10000000000000001
>>> s=0.0
>>> for i in range(10): s += 0.1
>>> s
0.99999999999999989
>>> print(s)
1.0

Примеры - Python
>>> import math
>>> a = math.sqrt(2)
>>> a
1.4142135623730951
>>> a*a == 2
False
>>> a*a
2.0000000000000004