Содержание
- 2. Закрепить понятие алгебраической дроби; Научить составлять математическую модель задачи; Научить находить значение алгебраической дроби, находить область
- 3. Примеры алгебраических дробей: Изучение новой темы Понятие алгебраической дроби известно из курса 7-го класса (сокращение дробей).
- 4. Иногда алгебраическое выражение по форме является – алгебраической дробью, а по существу – нет. Например: 20.06.2011
- 5. Решение Вывод: нельзя найти значение данной дроби при переменной х = 2 и при у =
- 6. Допустимые значения дроби – это такие значения, при которых знаменатель дроби не обращается в нуль. 20.06.2011
- 7. 20.06.2011 Кравченко Г. М. Алгоритм нахождения допустимых значений дроби: Находят значение переменной, при которых знаменатель дроби
- 8. 20.06.2011 Кравченко Г. М. Установите, при каких значениях переменной не имеет смысла алгебраическая дробь: Решение (3t
- 9. Установите, при каких значениях переменной не имеет смысла алгебраическая дробь: Решение 20.06.2011 Кравченко Г. М. Ответ:
- 10. Установите, при каких значениях переменной не имеет смысла алгебраическая дробь: Решение 20.06.2011 Кравченко Г. М. Ответ:
- 11. Найдите значение переменной, при которых равна нулю алгебраическая дробь: равно 0, если х - 4 =
- 12. 2. Задача. Лодка прошла по течению реки 10 км и против течения 6 км, затратив на
- 13. 2 этап. Работа с составленной математической моделью. 20.06.2011 Кравченко Г. М. 3 этап. Ответ на вопрос
- 14. Закрепление новой темы Является ли алгебраической дробью выражения: можно представить как многочлен является алгебраической дробью является
- 16. Скачать презентацию













 Intermediate
Intermediate Урок рисования
Урок рисования М. Е. Салтыков-Щедрин «История одного города». Замысел, история создания, жанр и композиция романа
М. Е. Салтыков-Щедрин «История одного города». Замысел, история создания, жанр и композиция романа Художник и ученый (9 класс)
Художник и ученый (9 класс) Политика как призвание и профессия
Политика как призвание и профессия Презентация на тему А. Герасимова «После дождя»
Презентация на тему А. Герасимова «После дождя» Русская душа Донбасса
Русская душа Донбасса Передача жилых домов в управление
Передача жилых домов в управление Художественная культура Древней Греции
Художественная культура Древней Греции Прекращение и расторжение трудового договора
Прекращение и расторжение трудового договора Служебные части речи
Служебные части речи Графическое решение физических задач
Графическое решение физических задач Создание сети социальной поддержки выпускников интернатных учреждений в период профессиональной подготовки
Создание сети социальной поддержки выпускников интернатных учреждений в период профессиональной подготовки Во что верят люди? Религия. Тема №2
Во что верят люди? Религия. Тема №2 ВЫХОДИ В ИНТЕРНЕТ!
ВЫХОДИ В ИНТЕРНЕТ!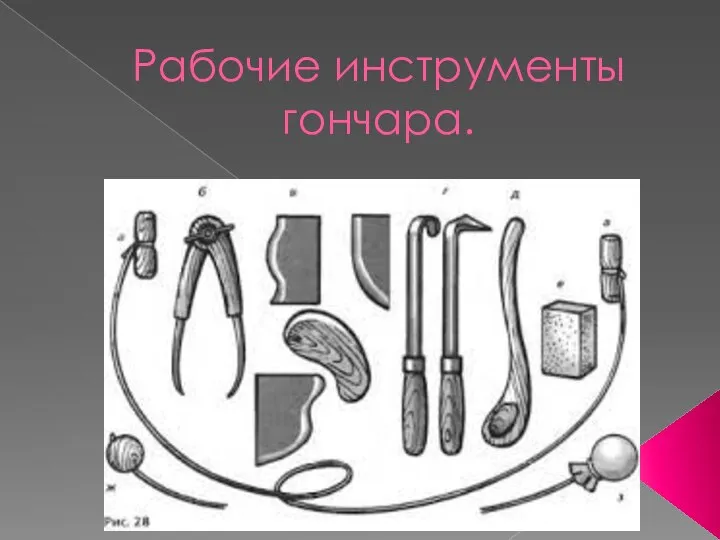 Рабочие инструменты гончара
Рабочие инструменты гончара Першагина Татьяна Юрьевна
Першагина Татьяна Юрьевна Художественные образы СПБ: российский город на перекрёстке мировых культур
Художественные образы СПБ: российский город на перекрёстке мировых культур Как стать богатым
Как стать богатым Ч Т О И З У Ч А Е Т
Ч Т О И З У Ч А Е Т Игры в eLearning
Игры в eLearning Презентация на тему Воды суши
Презентация на тему Воды суши порівняння чисел
порівняння чисел Представление о Power Point
Представление о Power Point Детские поделки на Пасху
Детские поделки на Пасху Муниципальной ресурсный центр «Система здоровьесберегающей деятельности в ОУ»
Муниципальной ресурсный центр «Система здоровьесберегающей деятельности в ОУ» Экологический кризис – глобальная проблема современности. На примере техногенных катастроф
Экологический кризис – глобальная проблема современности. На примере техногенных катастроф Молодёжь и политика
Молодёжь и политика