Презентация на тему Медианы, биссектрисы и высоты треугольника

Цели:
Цели урока:
ввести понятие перпендикуляра к прямой,
медианы, биссектрисы и высоты треугольника;
доказать теорему о перпендикуляре;
учитьcя строить медианы, биссектрисы и
высоты треугольника.

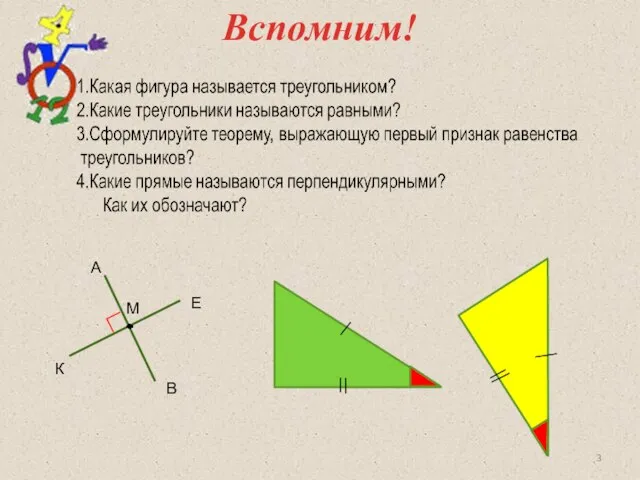
Вспомним!
∟

ПРОВЕРКА
ДОМАШНЕГО ЗАДАНИЯ
№ 97, № 98, № 99

а
Н
А
Изучение нового материала.
Построение перпендикуляра к прямой

Практическое задание
- Начертите прямую а и отметьте точку А,
- Через точку проведите прямую перпендикулярную прямой а.
- Точку пересечения обозначьте Н.
А
Н
а

Теорема о перпендикуляре
Из точки не лежащей на прямой можно провести перпендикуляр к этой прямой и притом один.

Докажем теорему о существовании
перпендикуляра к прямой.
Теорема: Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой и притом один.
Доказательство. Пусть A – точка, не лежащая на данной прямой a (рис. а).
Докажем сначала, что из точки A можно провести перпендикуляр к прямой a.
Мысленно перегнем плоскость по прямой a (рис. б) так, чтобы полуплоскость с границей a, содержащая точку A, наложилась на другую полуплоскость.
При этом точка A наложится на некоторую точку. Обозначим ее буквой B. Разогнем плоскость и проведем через точки A и B прямую.
Пусть H – точка пересечения прямых AB и a (рис. в). При повторном перегибании плоскости по прямой a точка H останется на месте. Поэтому луч HA наложится на луч HB, и, следовательно, угол 1 совместится с углом 2. Таким образом, ∠1 = ∠2. Так как углы 1 и 2 – смежные, то их сумма равна 180°, поэтому каждый из них – прямой. Следовательно, отрезок AH – перпендикуляр к прямой a.

Докажем, что из точки A можно провести
только один перпендикуляр к прямой .
Если предположить, что через точку A можно провести еще один перпендикуляр АН1 к прямой ВС, то получим, что две прямые АН и АН1, перпендикулярные к прямой ВС, пересекаются. Но в п.12 было доказано, что это невозможно (две прямые перпендикулярные к третьей не пересекаются.)
Итак, из точки А можно провести только один перпендикуляр к прямой АВ
Теорема доказана.
Н1

Медиана.
Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой треугольника . A
C
B
M

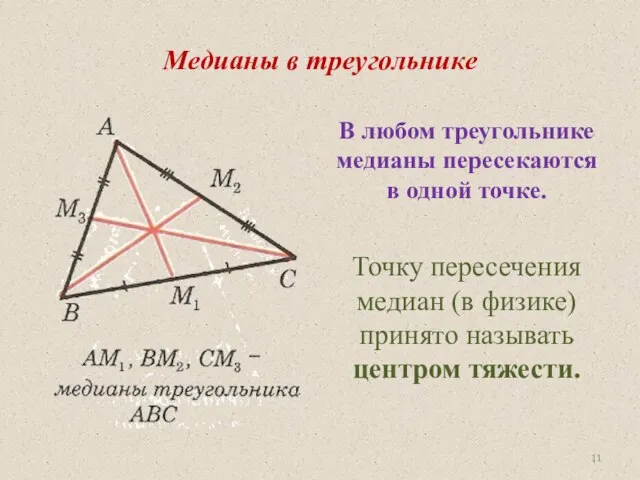
Медианы в треугольнике
В любом треугольнике медианы пересекаются в одной точке.
Точку пересечения медиан (в физике) принято называть центром тяжести.

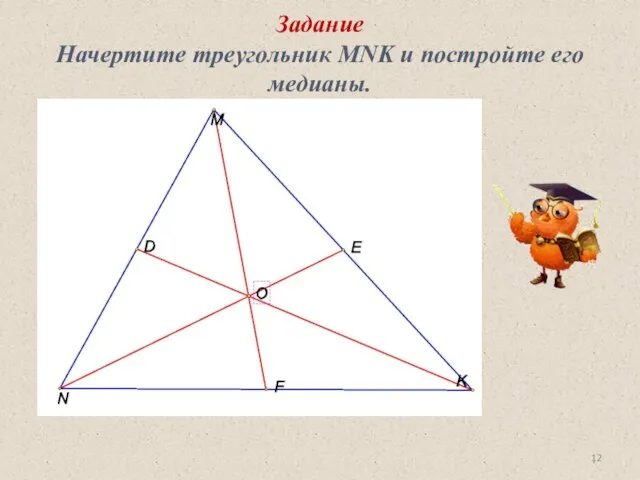
Задание
Начертите треугольник MNK и постройте его медианы.

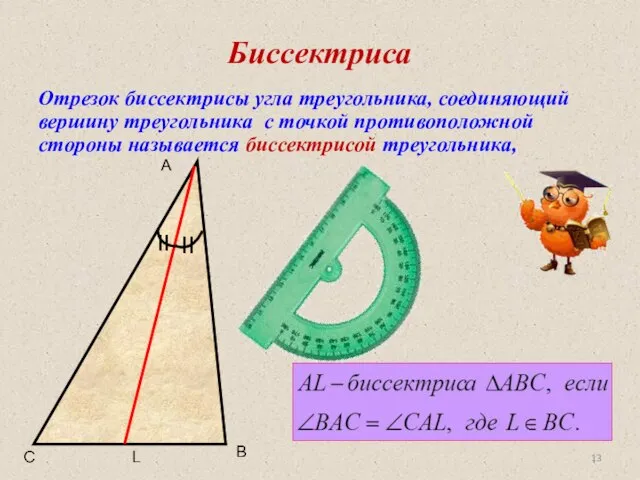
Биссектриса
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны называется биссектрисой треугольника,
A

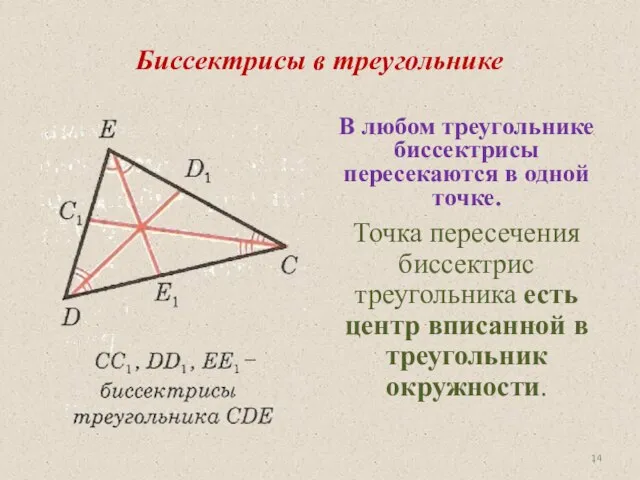
Биссектрисы в треугольнике
В любом треугольнике биссектрисы пересекаются в одной точке.
Точка пересечения биссектрис треугольника есть центр вписанной в треугольник окружности.

Задача
Начертите треугольник DEF и постройте его биссектрисы.

Высота
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону называется высотой треугольника

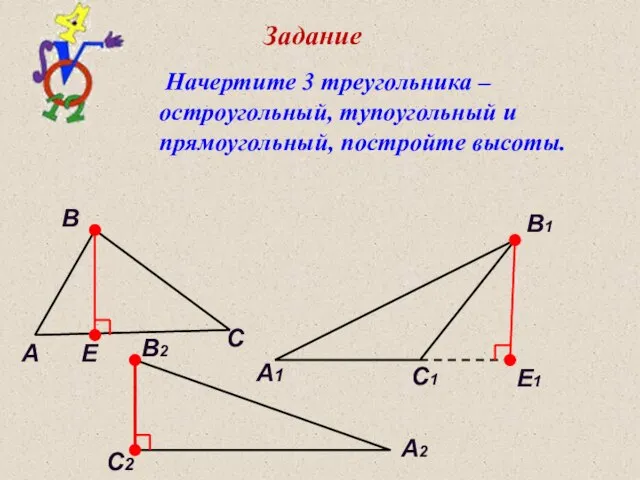
Задание
C
C1
C2
A
A1
A2
B
B1
B2
E
E1
Начертите 3 треугольника –
остроугольный, тупоугольный и
прямоугольный, постройте высоты.

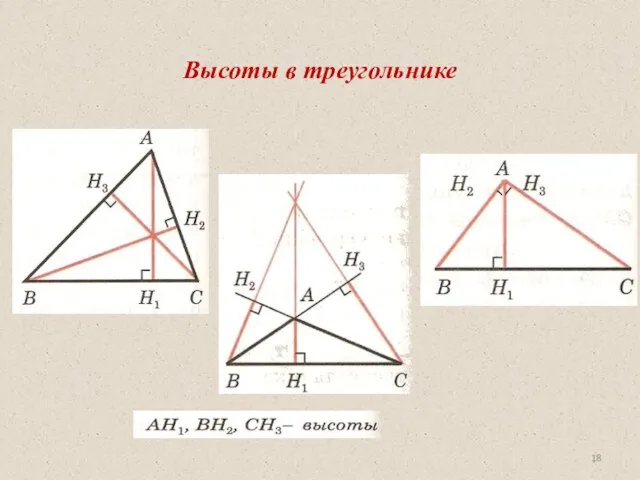
Высоты в треугольнике

Закрепление изученного материала
1.Решить задачи №105 (б), 106 (б) письменно.
2.Решите задания с самопроверкой
Дано: АО-медиана АВС, АО =ОК, АВ =6,3 см, ВС=6,5 см, АС =6,7 см. Найдите: СК
а)6,4 см; б) 6,7 см; в) 6,5 см; г) 6,3 см.
Дано: ОН и ОN - высоты МОК и ЕОF, ОН = ОN , ЕN = 7,8 см,
ОЕ= 8,6 см, НМ = 6,3 см. Найдите МК.
а)13, 9 см; б) 14,1 см; в) 14,9 см; г) 16,4 см.
В треугольниках АВС и КРМ проведены биссектрисы ВО и РЕ, причем АВО = КРЕ. Найдите отрезок ЕМ, если АС =9 см, а EM больше KE на 3,8 см.
а)6,4 см; б) 5,4 см; в) 2,6 см; г) 4,8 см.

Ответить на вопросы:
Какой отрезок называется перпендикуляром к прямой?
Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник?
Какой отрезок называется биссектрисой треугольника?
Сколько биссектрис имеет треугольник?
Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?