Слайд 2Цели урока :
Знакомство с прямой пропорциональностью и коэффициентом прямой пропорциональности;
Построение графика прямой

пропорциональности.
Слайд 3Исправьте ошибки, допущенные в написании математических терминов:
КОРДИНАТА
АБЦИСА
АРДИНАТА
ПРАПОРЦЫАНАЛЬ-НОСТЬ
ЛЕНЕЙНАЯ
ПРЕМАЯ
КОЭФИЦЕНТ

Слайд 4Является ли функция, заданная формулой линейной? Если да, то укажите коэффициенты k

Слайд 5Дана функция: y =–18x.
Принадлежат ли графику этой функции точки:
A(2; –36)
B(–1; –18)
C(0; 0)
D(–2;

9)
Слайд 6Какой формулой записывается линейная функция?
y = kx + b
Если b =

0, то какой вид примет линейная функция?
y = kx
Слайд 7Определение
Прямой пропорциональностью называется функция вида y=kx, где x – независимая переменная, а

k – неравное нулю число.
Примеры:
y=2x
y=-2x
y=-0,5x
y=1/3x
Слайд 8Примеры прямой пропорциональности
1) S=60t (путь, v=60 км/ч)
2) S=40b (площадь прямоугольника со

стороной 40 см)
3) m=19,3 V (масса бруска золота с плотностью 19,3 г/см3)
4) C=10n (С – стоимость, n – количество товара по цене 10 рублей)
Слайд 9График функции
В прямоугольной системе координат выполните построение графиков функций:
y=x
y=4x
y=–3x

Слайд 10Так как прямая пропорциональность является частным случаем линейной функции, то графиком является

прямая. Для построения прямой нужно знать координаты двух точек.
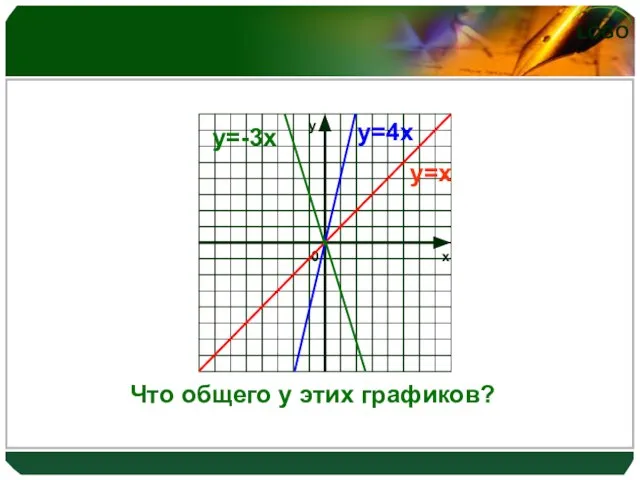
Слайд 11у=х
у=4х
у=-3х
Что общего у этих графиков?
Слайд 12 Графиком функции y=kx является прямая, проходящая через начало координат (0; 0)

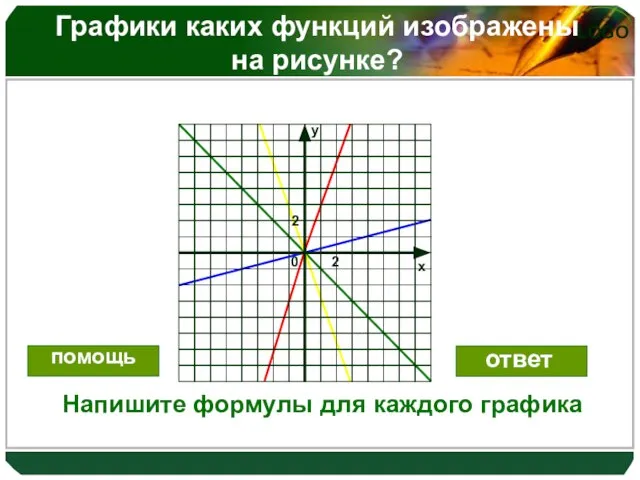
Слайд 13Графики каких функций изображены на рисунке?
Напишите формулы для каждого графика
Слайд 14Так как прямые проходят через начало координат, то функция - прямая пропорциональность.
Точка

А (1;3) принадлежит прямой, значит ее координаты удовлетворяют формуле у=кх.
Получаем уравнение 3=к·1, т.е. к=3.
Функция задается формулой у=3х.
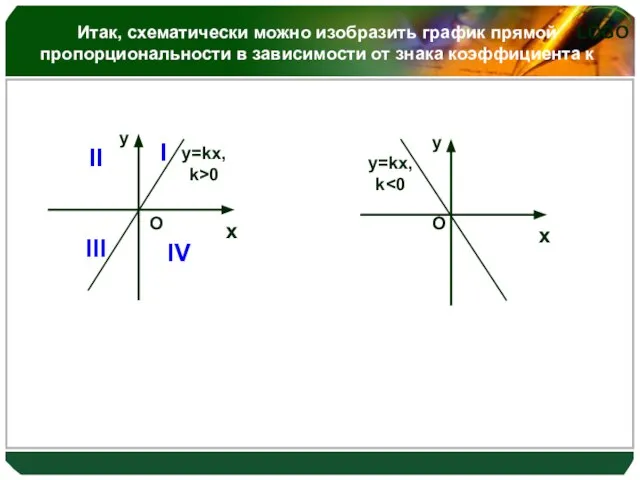
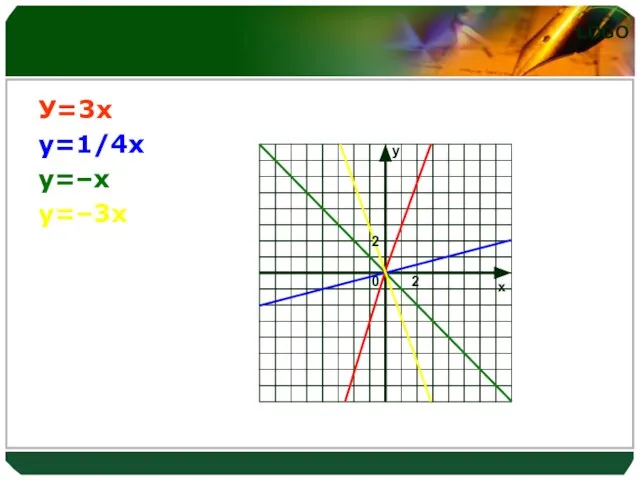
Слайд 16Итак, схематически можно изобразить график прямой пропорциональности в зависимости от знака коэффициента














 Материалы для подготовки к контрольной работе по теме Греция
Материалы для подготовки к контрольной работе по теме Греция Управление человеческими ресурсами
Управление человеческими ресурсами Администрирование почтового сервера
Администрирование почтового сервера Загробная жизнь в Древнем Египте: гробницы и саркофаги.
Загробная жизнь в Древнем Египте: гробницы и саркофаги. Учимся письменному пересказу
Учимся письменному пересказу ОБЩЕСТВЕННАЯ ПАЛАТА ОМСКОЙ ОБЛАСТИ ОБЩЕСТВЕННЫЕ СЛУШАНИЯ «ОБ УСТАНОВКЕ ПАМЯТНИКА А.В. КОЛЧАКУ В г. ОМСКЕ» 19 июля 2012 года
ОБЩЕСТВЕННАЯ ПАЛАТА ОМСКОЙ ОБЛАСТИ ОБЩЕСТВЕННЫЕ СЛУШАНИЯ «ОБ УСТАНОВКЕ ПАМЯТНИКА А.В. КОЛЧАКУ В г. ОМСКЕ» 19 июля 2012 года  2.1.1. Содержание и последствия промышленного переворота для мировой экономики. 2.1.2. Англия – родина промышленной революции. 2.1.3. Кап
2.1.1. Содержание и последствия промышленного переворота для мировой экономики. 2.1.2. Англия – родина промышленной революции. 2.1.3. Кап Отношение к красоте человеческого тела как к великой ценности, данной природой, на протяжении многовековой истории человеческого
Отношение к красоте человеческого тела как к великой ценности, данной природой, на протяжении многовековой истории человеческого  Михаил Тариелович Лорис-Меликов
Михаил Тариелович Лорис-Меликов 11. Четвертый шаг – планирование исследования. Во всяком деле, чтобы добиться успеха, нужна некоторая доля безумия. Шекспир Уилья
11. Четвертый шаг – планирование исследования. Во всяком деле, чтобы добиться успеха, нужна некоторая доля безумия. Шекспир Уилья Презентация на тему Московский Кремль
Презентация на тему Московский Кремль  МК-Малая академия-2019 (новые филиалы без ЛЛ) (4)
МК-Малая академия-2019 (новые филиалы без ЛЛ) (4) Спирты и фенолы
Спирты и фенолы Что такое биомеханика
Что такое биомеханика  Презентация на тему Природная зональность
Презентация на тему Природная зональность  Урок-олимпиада «Кто хочет стать грамотным?»
Урок-олимпиада «Кто хочет стать грамотным?» Анализ социального института собеседования при приеме на работу
Анализ социального института собеседования при приеме на работу Nightrider
Nightrider Г.Цыферов «Как цыплёнок впервые сочинил сказку»
Г.Цыферов «Как цыплёнок впервые сочинил сказку» Якутское национальное блюдо саламат
Якутское национальное блюдо саламат Wildlife of the UK
Wildlife of the UK Что мы знаем о Солнце?
Что мы знаем о Солнце? Роль баскетбола в развитии физического качества ловкость у учащихся среднего школьного возраста
Роль баскетбола в развитии физического качества ловкость у учащихся среднего школьного возраста САПР
САПР Компонентная среда разработки инструментария нагрузочного тестирования
Компонентная среда разработки инструментария нагрузочного тестирования Компетентность, универсальные учебные действия и практика проектирования учебного процесса
Компетентность, универсальные учебные действия и практика проектирования учебного процесса Изменение климата
Изменение климата Тема 2.2 Поводження із психічно хворими людьми
Тема 2.2 Поводження із психічно хворими людьми