Презентация на тему Силы в природе

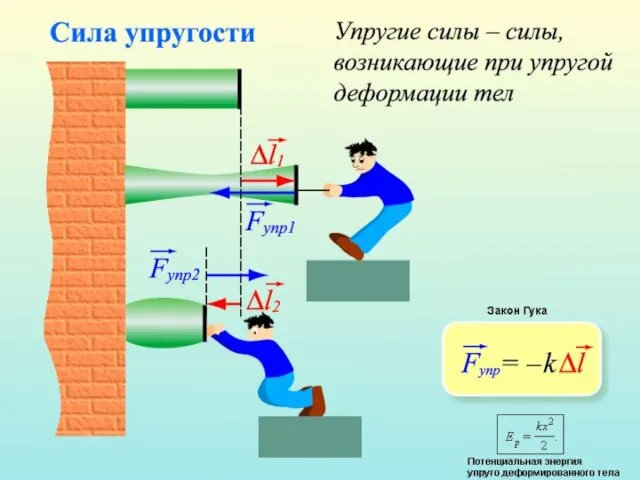
Силой упругости называют силу, которая возникает в теле при изменении его формы или размеров.
Это происходит, если тело сжимают, растягивают, изгибают или скручивают.
Сила упругости

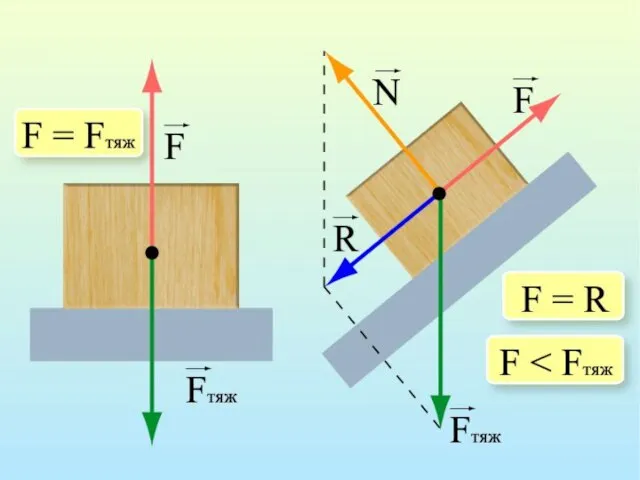
Сила тяжести
Разновидностью силы тяготения является сила тяжести – сила, с которой тело, находящееся вблизи какой-либо планеты, притягивается к ней.

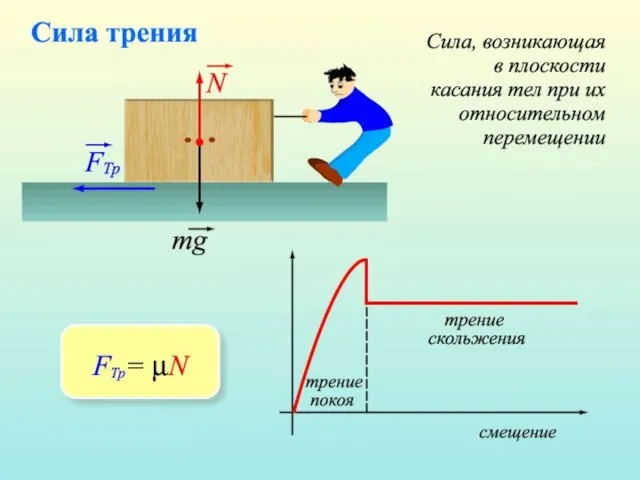
Сила трения
Силой трения называют силу, препятствующую проскальзыванию одного тела по поверхности другого.
Резкое торможение автомобиля сопровождается "визгом тормозов". Он возникает из-за проскальзывания шин по поверхности асфальта. При этом между колесом и дорогой действует сила трения, препятствующая такому проскальзыванию.

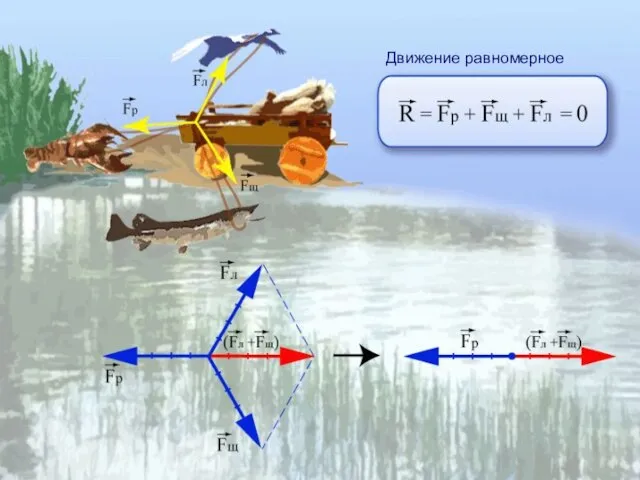
Движение равномерное

Выталкивающая сила
Выталкивающей силой (или силой Архимеда) называют силу, с которой жидкость или газ действуют на погруженное в них тело.
Архимедова сила обычно
направлена вверх,
противоположно силе
тяжести.

Вес и невесомость
Вес - это сила, с которой тело действует на опору

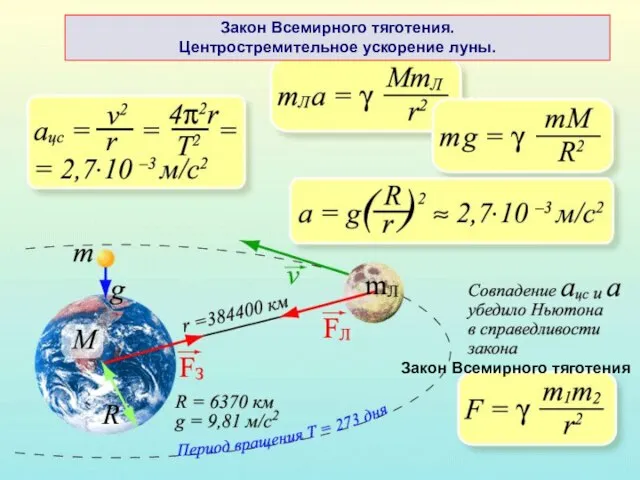
Закон Всемирного тяготения
Закон Всемирного тяготения.
Центростремительное ускорение луны.

ЗАДАЧА:
В результате полученного толчка кирпич начал скользить вниз по неподвижной ленте конвейера, расположенной под углом α=30о к горизонтальной плоскости. Определите величину и направление ускорения кирпича , если коэффициент трения скольжения кирпича о ленту конвейера µ=0,6.

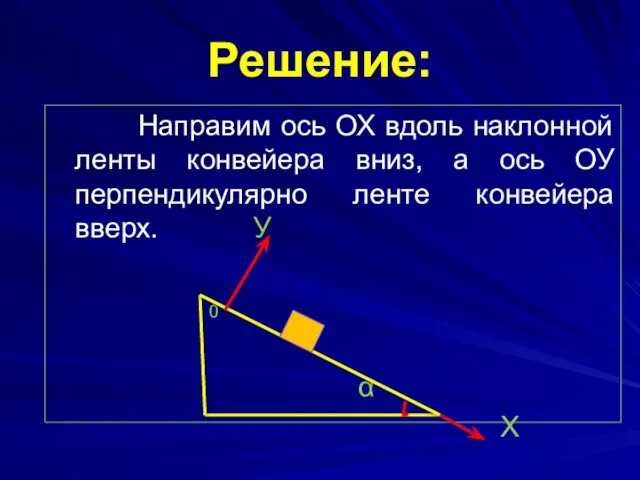
Решение:
Направим ось ОХ вдоль наклонной ленты конвейера вниз, а ось ОУ перпендикулярно ленте конвейера вверх. У
0
α
Х

Так как кирпич движется вдоль оси ОХ, то его ускорение может быть направлено только вдоль этой оси вниз либо вверх.
а
а
У
Х
0
α

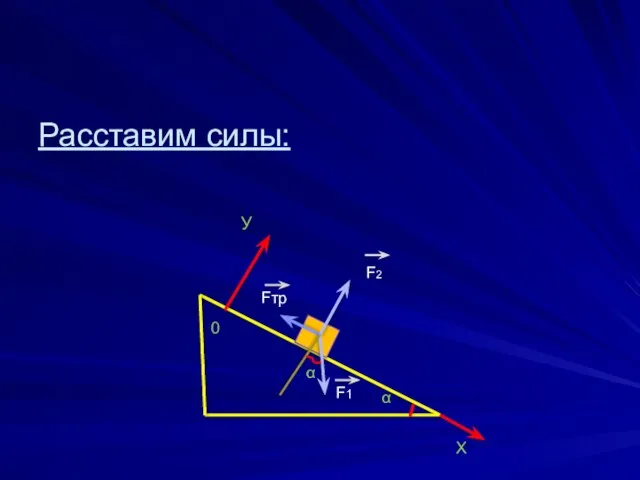
Расставим силы:
Fтр
F2
F1
α
0
Х
У
α

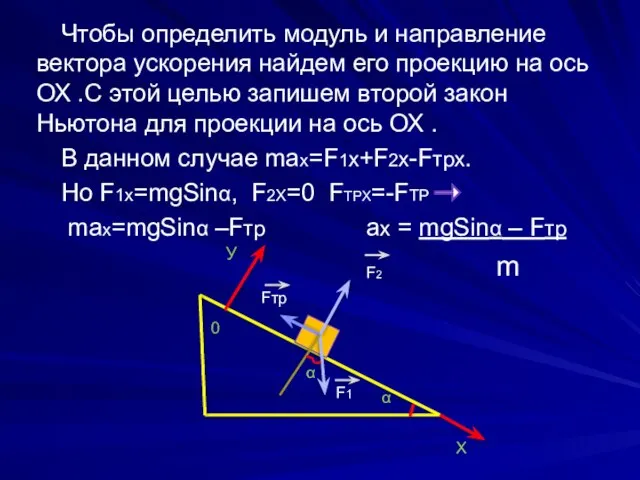
Чтобы определить модуль и направление вектора ускорения найдем его проекцию на ось ОХ .С этой целью запишем второй закон Ньютона для проекции на ось ОХ .
В данном случае maх=F1х+F2х-Fтрх.
Но F1х=mgSinα, F2X=0 FТРХ=-FТР
max=mgSinα –Fтр aх = mgSinα – Fтр
m
Fтр
F2
F1
α
0
Х
У
α

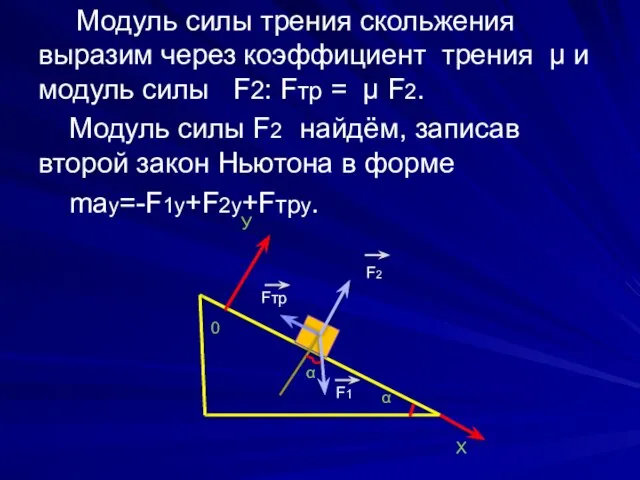
Модуль силы трения скольжения выразим через коэффициент трения µ и модуль силы F2: Fтр = µ F2.
Модуль силы F2 найдём, записав второй закон Ньютона в форме
maу=-F1у+F2у+Fтру.
Fтр
F2
F1
α
0
Х
У
α

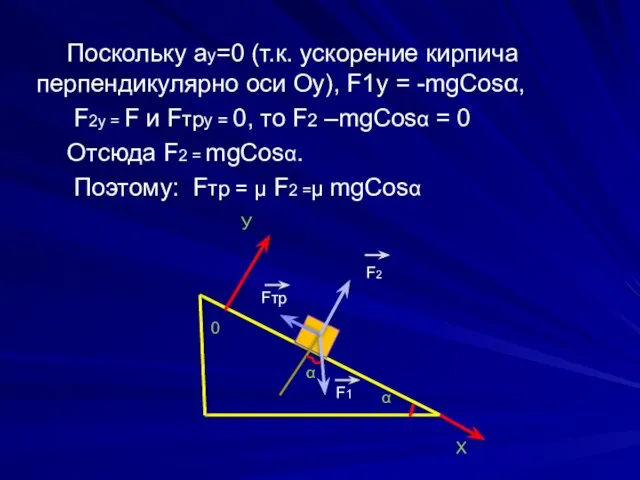
Поскольку ау=0 (т.к. ускорение кирпича перпендикулярно оси Оу), F1у = -mgСosα, F2у = F и Fтру = 0, то F2 –mgСosα = 0
Отсюда F2 = mgСosα.
Поэтому: Fтр = µ F2 =µ mgСosα
Fтр
F2
F1
α
0
Х
У
α

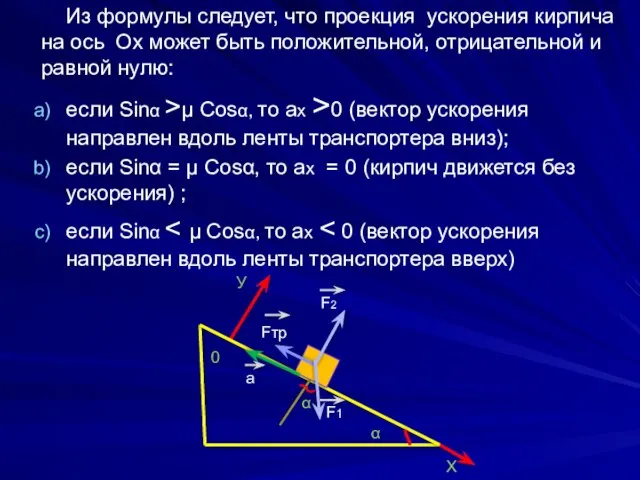
Из формулы следует, что проекция ускорения кирпича на ось Ох может быть положительной, отрицательной и равной нулю:
если Sinα >µ Сosα, то aх >0 (вектор ускорения направлен вдоль ленты транспортера вниз);
если Sinα = µ Сosα, то aх = 0 (кирпич движется без ускорения) ;
если Sinα < µ Сosα, то aх < 0 (вектор ускорения направлен вдоль ленты транспортера вверх)
0
α
α
У
Х
Fтр
F2
F1
a

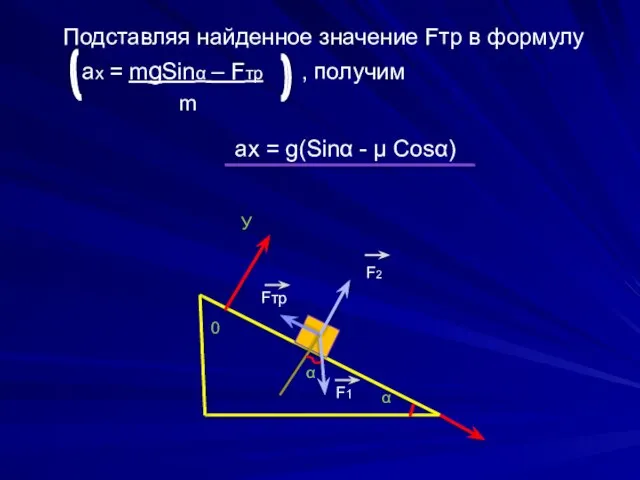
Подставляя найденное значение Fтр в формулу
aх = mgSinα – Fтр , получим
m
aх = g(Sinα - µ Сosα)
Fтр
F2
F1
α
0
У
α