Содержание
- 2. Цели: 19.09.2012 Повторить понятие треугольника и его элементов. Ввести понятие равных треугольников. Применять полученные знания при
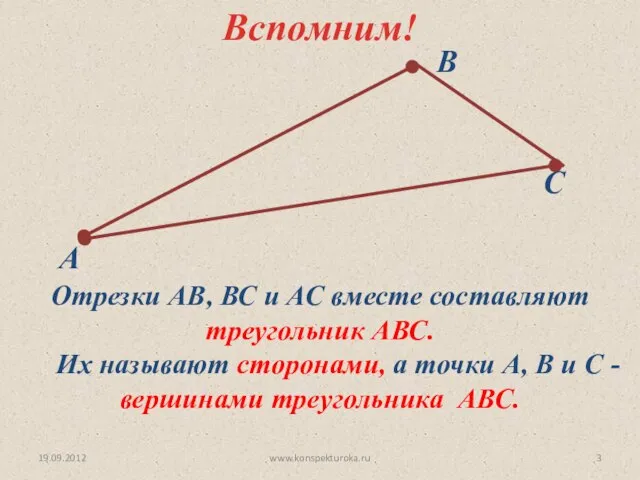
- 3. 19.09.2012 www.konspekturoka.ru Отрезки АВ, ВС и АС вместе составляют треугольник АВС. Их называют сторонами, а точки
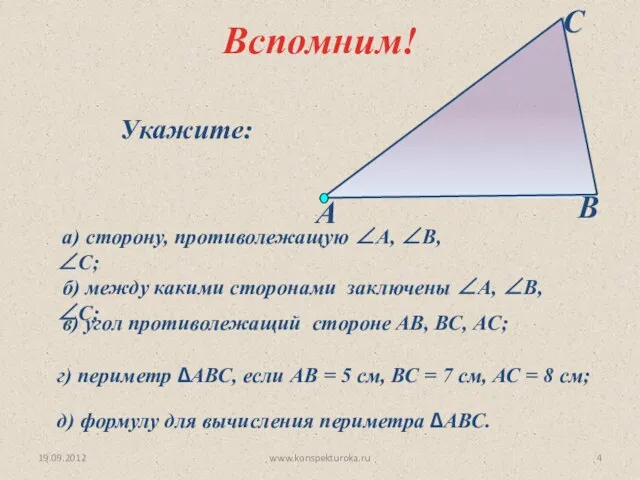
- 4. 19.09.2012 www.konspekturoka.ru Вспомним! Укажите: а) сторону, противолежащую ∠А, ∠В, ∠С; б) между какими сторонами заключены ∠А,
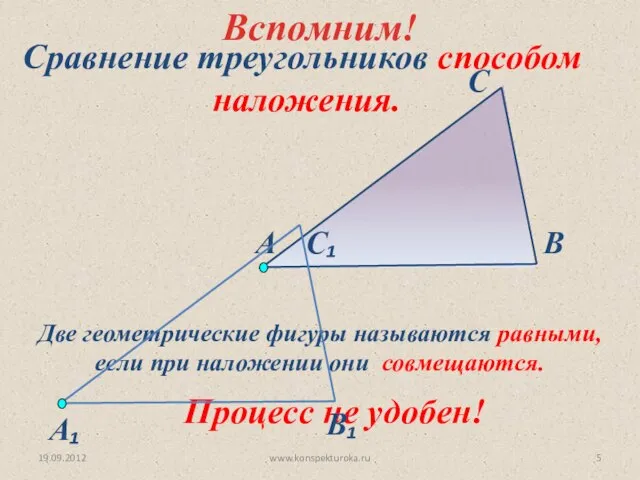
- 5. 19.09.2012 www.konspekturoka.ru Две геометрические фигуры называются равными, если при наложении они совмещаются. Сравнение треугольников способом наложения.
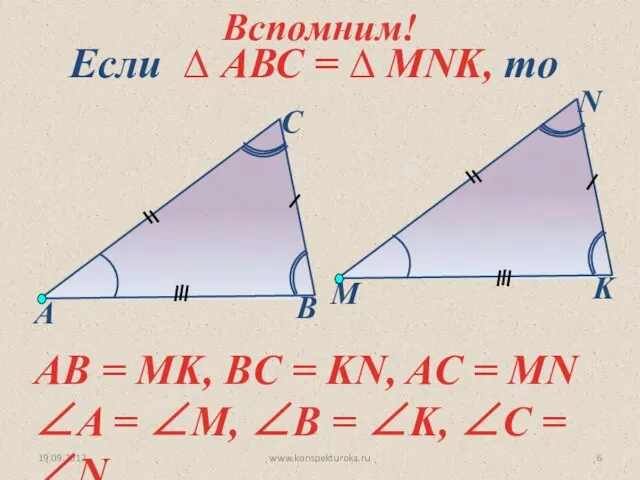
- 6. 19.09.2012 www.konspekturoka.ru Если ∆ АВС = ∆ MNK, то АВ = MK, BС = KN, AC
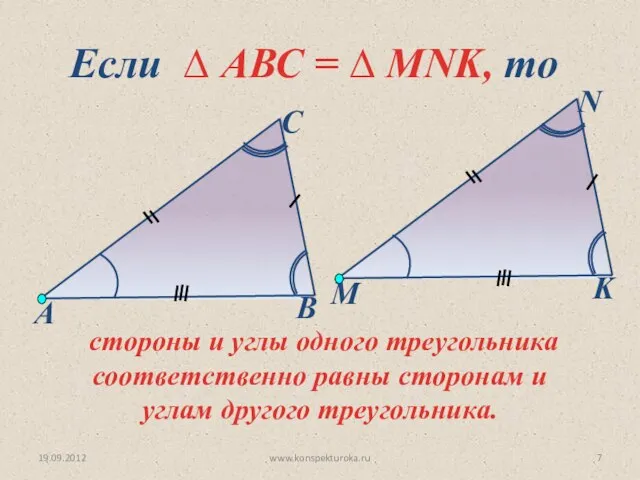
- 7. 19.09.2012 www.konspekturoka.ru Если ∆ АВС = ∆ MNK, то стороны и углы одного треугольника соответственно равны
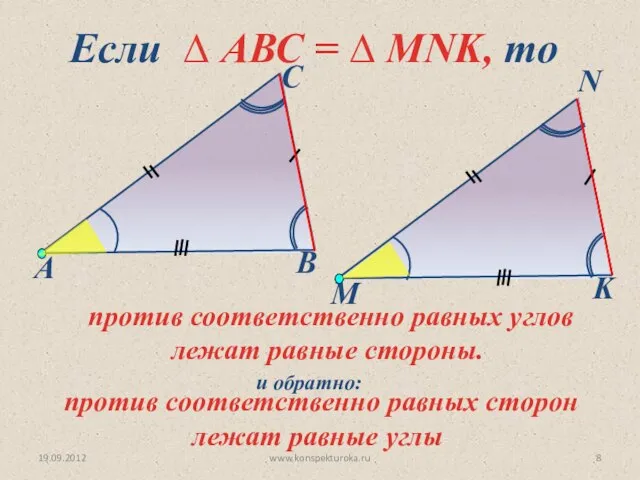
- 8. 19.09.2012 www.konspekturoka.ru Если ∆ АВС = ∆ MNK, то против соответственно равных сторон лежат равные углы
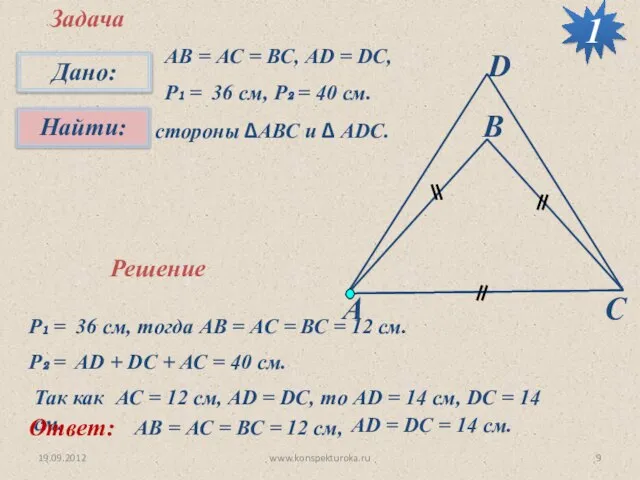
- 9. 19.09.2012 www.konspekturoka.ru Задача Решение АВ = АС = ВС, АD = DC, P₁ = 36 см,
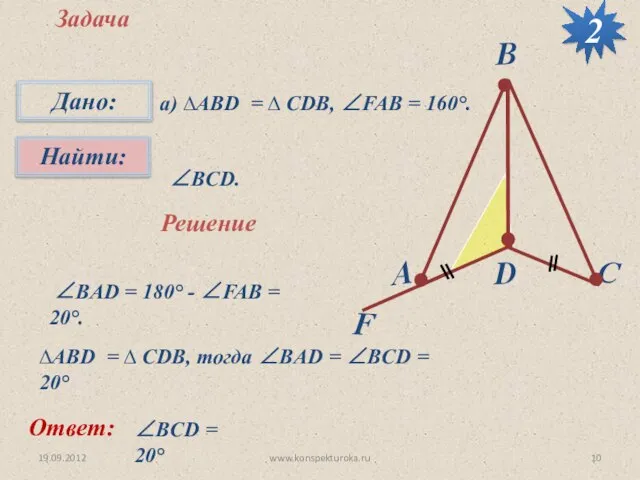
- 10. 19.09.2012 www.konspekturoka.ru Задача а) ∆АВD = ∆ CDB, ∠FAB = 160°. ∠BCD. Решение ∠BAD = 180°
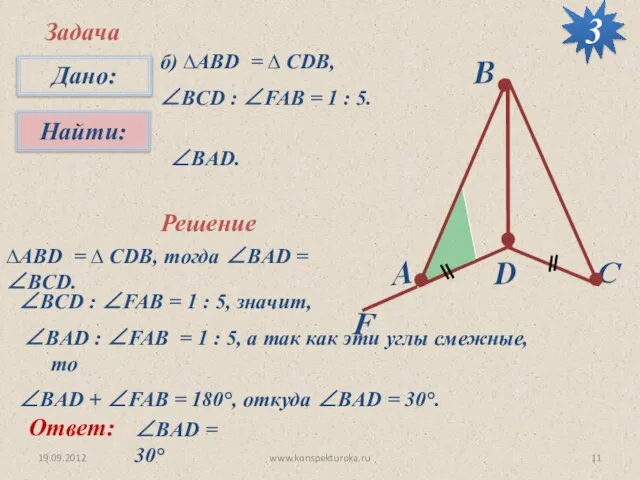
- 11. 19.09.2012 www.konspekturoka.ru Задача б) ∆АВD = ∆ CDB, ∠BCD : ∠FAB = 1 : 5. ∠BАD.
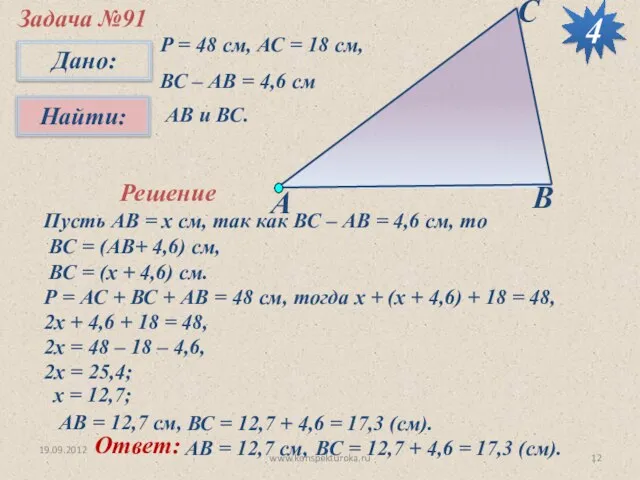
- 12. 19.09.2012 Задача №91 Р = 48 см, АС = 18 см, ВС – АВ = 4,6
- 14. Скачать презентацию

 Путешествие по "Стране Законии"
Путешествие по "Стране Законии" Логарифмическая функция, ее свойства и график. Логарифмическая спираль
Логарифмическая функция, ее свойства и график. Логарифмическая спираль История радиоуправления. Лекция 6
История радиоуправления. Лекция 6 Продвижение приложений в Моем Мире и Одноклассниках Роман Новиков Платформа@Mail.Ru
Продвижение приложений в Моем Мире и Одноклассниках Роман Новиков Платформа@Mail.Ru Модели олигополии: обзор. Часть 2. Олигополия со сговором. Олигополия с барьерами входа
Модели олигополии: обзор. Часть 2. Олигополия со сговором. Олигополия с барьерами входа Активизация познавательных процессов младших школьников Учитель средней школы № 43 Жолудева А. В.
Активизация познавательных процессов младших школьников Учитель средней школы № 43 Жолудева А. В. Виды энергии
Виды энергии Нам всем уютно в нашем 8а!
Нам всем уютно в нашем 8а! Светлана Дружкова. Работы
Светлана Дружкова. Работы Рисование геометрического орнамента в квадрате
Рисование геометрического орнамента в квадрате О стилях семейного воспитания Родительское собрание 2 класс
О стилях семейного воспитания Родительское собрание 2 класс Анализ бухгалтерской отчетности общества с ограниченной ответственностью Кока - Кола Софт Дринк Консалтинг
Анализ бухгалтерской отчетности общества с ограниченной ответственностью Кока - Кола Софт Дринк Консалтинг Представление о мультимедийных продуктах
Представление о мультимедийных продуктах The British museam library
The British museam library 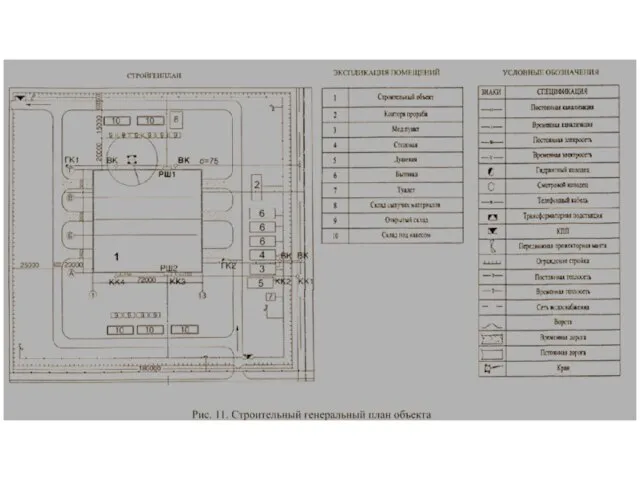 Технологическое проектирование строительных процессов. Стройтехплан
Технологическое проектирование строительных процессов. Стройтехплан Службы сопровождения в коррекционно-развивающем образовании. Уровни сопровождения системный и индивидуальный
Службы сопровождения в коррекционно-развивающем образовании. Уровни сопровождения системный и индивидуальный Итоги деятельности ОАО «Ярославская электросетевая компания» за 2009 год
Итоги деятельности ОАО «Ярославская электросетевая компания» за 2009 год Презентация на тему Информационное обеспечение международной перевозки грузов
Презентация на тему Информационное обеспечение международной перевозки грузов  Vrais amis
Vrais amis Сущность понятия
Сущность понятия Лаборатория юного исследователя за 2020-2021 уч. год
Лаборатория юного исследователя за 2020-2021 уч. год GLOBAL SOLUTIONS LTD. Регус Капитал Плаза125047, Москва,4й Лесной пер., д. 4,тел. +7 495 641 37 20факс +7 495 225 85
GLOBAL SOLUTIONS LTD. Регус Капитал Плаза125047, Москва,4й Лесной пер., д. 4,тел. +7 495 641 37 20факс +7 495 225 85  Презентация на тему Викторина по Франции
Презентация на тему Викторина по Франции Семантика слова
Семантика слова Растениеводство в нашем крае
Растениеводство в нашем крае Профильное обучение и предпрофильная подготовка как ресурс социально-экономического развития Санкт-Петербурга.
Профильное обучение и предпрофильная подготовка как ресурс социально-экономического развития Санкт-Петербурга. Авиатехника 1 звук
Авиатехника 1 звук Конфликт – столкновение двух или более сторон с целью реализации их интересов в условиях противодействия
Конфликт – столкновение двух или более сторон с целью реализации их интересов в условиях противодействия