Слайд 2Решение линейных уравнений, содержащиx неизвестное под знаком модуля
Толька с алгебры начинается строгое

математическое учение. (Н.И.Лобачевский)
Слайд 3
При решении уравнений, содержащих несколько выражений со знаком модуля, удобнее пользоваться алгебраическим

определением модуля числа: модулем положительного числа и нуля является само число, модулем отрицательного числа называется противоположное ему положительное число.
Слайд 4Решим уравнение:
│2х-12│+│6х+48│= 160.
Решение:
а) Найдем корни каждого выражения, содержащего знак модуля:
2х-12=0, х=6
6х+48=0, х

= -8
Слайд 5б) Найденные значения х разбивают числовую прямую на три промежутка: х< -8;

-8≤x≤6; x>6. Решение данного уравнения рассматриваем в каждом промежутке отдельно.
_Ι_________ΙΙ__________ΙΙΙ____ -8 6
Слайд 6в) Ι. Х< -8
-(2x-12)-(6x+48)=160
-2x+12 -6x-48=160
-8x=196
х=- 24,5 (x<-8)
В

данном промежутке оба выражения, стоящее под знаком модуля, отрицательны.
Слайд 7ΙΙ -8≤х≤6
В данном промежутке первое выражение, стоящие под знаком модуля, отрицательно,

а второе положительное.
-(2x-12)+(6x+48)=160
-2x+12+6x+48=160
4x=100
x =25 ( не принадлежит данному промежутку)
Слайд 8ΙΙΙ х>6
Оба выражения, стоящие под знаком модуля, положительны.
(2x-12)+(6x+48)=160
2x-12+6x+48=160
8x=124

x=15,8 (x>6)
Ответ: -24,5; 15,8
Слайд 9Решите уравнение:
а) │3-х│=7
б) │2х-5│=39
в) │84-5х│=64
г) │28х-37│=93
д) │56-8х│+│36х+144│=356
е) │2х-16│+│5х+20│+│3х-30│=300
ж) │15х-105│+│12х-288│=535









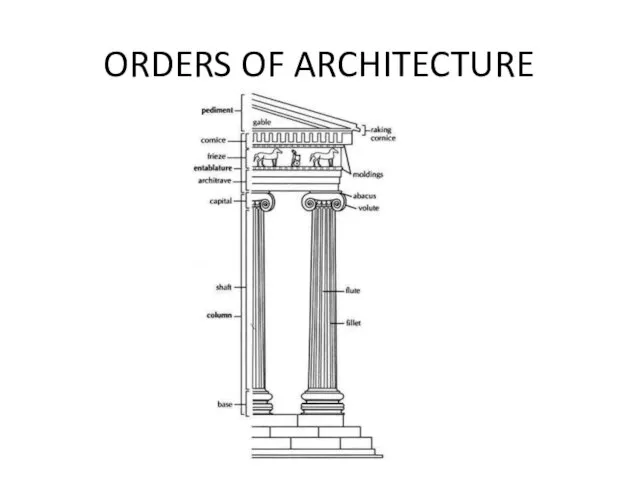 ORDERS OF ARCHITECTURE
ORDERS OF ARCHITECTURE Кабельные системы обогрева в строительстве
Кабельные системы обогрева в строительстве Презентация на тему Жаркие пустыни
Презентация на тему Жаркие пустыни Воронцов А.Б. 21 мая 2010
Воронцов А.Б. 21 мая 2010 Имидж, поведение и репутация как фактор жизненного успеха
Имидж, поведение и репутация как фактор жизненного успеха День матери
День матери Пингвины
Пингвины Политическая власть. Тема 3
Политическая власть. Тема 3 Разработка электрической винто-моторной группы для лёгкого летательного аппарата
Разработка электрической винто-моторной группы для лёгкого летательного аппарата  Детское воскресное служение
Детское воскресное служение Технология кислородной резки
Технология кислородной резки История вышивки лентами
История вышивки лентами 11 Программа развития МБСКОУ СКОШ 3 VIII вида г. Ишима на 2012 – 2014 гг. Департамент по социальным вопросам администрации г. Ишима Муницип
11 Программа развития МБСКОУ СКОШ 3 VIII вида г. Ишима на 2012 – 2014 гг. Департамент по социальным вопросам администрации г. Ишима Муницип Решение задач на движение
Решение задач на движение Olympiade in der Schule
Olympiade in der Schule Имущественные права личного характера в российском гражданском праве
Имущественные права личного характера в российском гражданском праве Ежегодно команда юношей принимает участиев межрегиональных соревнованиях среди кадетских корпусов, православных гимназий, дет
Ежегодно команда юношей принимает участиев межрегиональных соревнованиях среди кадетских корпусов, православных гимназий, дет Традиции Бурятии
Традиции Бурятии Сайт, который продает. Интернет магазин – это легко!
Сайт, который продает. Интернет магазин – это легко! Применение СУП в командной работе
Применение СУП в командной работе Н.В. Гоголь «Женитьба»
Н.В. Гоголь «Женитьба» Девиантное поведение
Девиантное поведение Педагогическая компетентность учителя как результат самообразования
Педагогическая компетентность учителя как результат самообразования Натюрморт с чучелом птицы
Натюрморт с чучелом птицы Право на оружие
Право на оружие "Ты не одинока"
"Ты не одинока" Курсы дистанционного обучения для электроэнергетики
Курсы дистанционного обучения для электроэнергетики Церковь Иль-Джезу
Церковь Иль-Джезу