Принципы возможных перемещений, обобщенные координатные системы

1. Связи и их уравнения.
Связями принято называть ограничения, налагаемые на положения и скорости точек механической системы, которые должны выполняться при любых действующих на систему силах. Если на перемещения системы не наложено никаких ограничений или связей, она называется свободной системой. При наличии одной или нескольких связей она становится несвободной системой.
Уравнения, которым из-за наложенных связей должны удовлетворять координаты точек механической системы и их скорости (первые производные от координат по времени), принято называть уравнениями связей.
В общем случае уравнение связи имеет вид:
Функция f предполагается дважды непрерывно дифференцируемой.
Например, если материальная точка может перемещаться только в некоторой плоскости, совпадающей с плоскостью Оху декартовой системы координат, то уравнением связи будет z=0.

Предположим, точка перемещается по сфере, радиус которой изменяется во времени:
R =f (t).Если центр сферы совпадает с началом координат, а х, у, z — координаты движущейся точки, то уравнение связи
В зависимости от вида функции (1) связи подразделяют на:
1) геометрические и дифференциальные;
2) голономные и неголономные;
3) стационарные и нестационарные;
4) удерживающие и неудерживающие.
К геометрическим связям относят такие связи, уравнения которых содержат только координаты точек механической системы (и, может быть, время).

Дифференциальными связями считают связи, уравнения которых, кроме координат точек механической системы, содержат и первые производные от этих координат по времени (и, может быть, время). Примеры дифференциальных связей: связи конька при движении его по льду, связи колеса при качении его без скольжения по некоторой поверхности.
Геометрические связи и дифференциальные связи, уравнения которых могут быть проинтегрированы, называются голономными связями.
Неголономными связями принято называть дифференциальные связи, уравнения которых не могут быть проинтегрированы.
В качестве примера рассмотрим качение диска по наклонной плоскости без скольжения

Положение диска определяется координатой хс центра С диска и углом поворота
При качении выполняется соотношение
или
,
т. е. получить зависимость между координатами, определяющими положение диска. Таким образом, рассматриваемая связь — голономная.
Связи, в уравнения которых время явно не входит, называются стационарными связями, а в противном случае — нестационарными связями
Конструктивно связи осуществляют в виде поверхностей, стержней, нитей, шарниров, направляющих и др.

2. Принцип возможных перемещений.
Возможные перемещения. В статике действие связей учитывают их реакциями. Однако вместо реакций можно рассматривать перемещения, допускаемые связями. Тогда и в уравнениях равновесия (движения) механической системы не будет неизвестных реакций связей.
Когда материальная, точка Р под действием приложенных сил перемещается по поверхности, движущейся в системе координат Oxyz, поверхность, уравнение которой
, (2.2)
является для точки Р удерживающей, нестационарной и голономной связью.

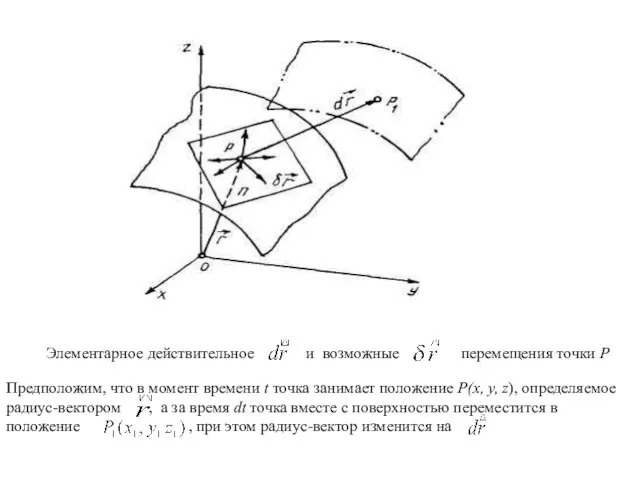
Элементарное действительное
и возможные
перемещения точки Р
Предположим, что в момент времени t точка занимает положение Р(х, у, z), определяемое радиус-вектором , а за время dt точка вместе с поверхностью переместится в положение , при этом радиус-вектор изменится на

Перемещение точки из одного положения в другое, бесконечно близкое к первому, выражаемое дифференциалом радиус-вектора точки, представляет собой элементарное перемещение точки:
Вектор
действительное перемещение точки, направлен по касательной к траектории точки, так как
=
Если в некоторый момент времени t сообщить точке воображаемое малое перемещение, допускаемое ее связями, то радиус-вектор
точки Р получит малое приращение
называемое изохронной вариацией радиус-вектора точки. Это название отражает то, что изменение радиус-вектора происходит изохронно t.
Любое допускаемое наложенными связями элементарное перемещение материальной точки из положения, занимаемого ею в некоторый момент времени, выражаемое изохронной вариацией радиус-вектора этой точки, называется возможным или виртуальным перемещением точки:
Возможные перемещения
точки представляют собой воображаемые малые перемещения, которые она могла бы совершать из данного положения без нарушения наложенных связей при отсутствии действующих на точку сил при остановленном времени.

Возможное, или виртуальное, перемещение механической системы — это любая совокупность возможных перемещений точек данной системы, допускаемая всеми наложенными на нее связями.
Возможные перемещения системы или твердого тела должны удовлетворять двум условиям:
1) быть малыми, чтобы конфигурация системы и ее положение в пространстве оставались неизменными;
2) связи, наложенные на систему, не должны нарушаться при ее возможных перемещениях.
Например, возможное перемещение рычага АВ — поворот его на элементарный угол
относительно точки О. При таком повороте точки А и В перемещаются по дугам
окружностей
Эти перемещения с точностью до величины первого порядка малости можно заменить возможными перемещениями
в виде прямолинейных отрезков на касательных к траекториям точек

Любая механическая система может иметь множество возможных перемещений, среди которых можно выделить некоторое число перемещений, не зависящих одно от другого.
Так, если для рычага АВ за независимое возможное перемещение принять вектор
то возможное перемещение точки С, например, можно выразить через
следующим образом:
Модули возможных перемещений точек рычага пропорциональны расстояниям от них до оси поворота.
Число независимых между собой возможных перемещений механической системы называется числом степеней свободы этой системы.
Число степеней свободы механической системы с геометрическими связями равно числу независимых координат, описывающих положение этой системы.
Число степеней свободы механической системы.

Некоторые примеры.
1).Свободная точка в пространстве имеет три степени свободы. Независимыми являются три возможных перемещения точки вдоль трех координатных осей; положение точки определяется тремя независимыми координатами, например х, у, z.
2).Материальная точка при движении по поверхности обладает двумя степенями свободы. Ее положение на поверхности определяется двумя независимыми координатами.
3).Свободное твердое тело в пространстве имеет шесть степеней свободы. Оно может перемещаться вдоль координатных осей и поворачиваться относительно этих осей.
Обобщенные координаты. Рассмотрим механическую систему из п материальных точек
на которые наложено l голономных связей
Положение этой системы в пространстве может быть задано 3п декартовыми координатами, которые к тому же должны удовлетворять l уравнениям связей. Следовательно, число независимых координат
s = 3п — l.
Независимые между собой параметры, которые при наименьшем числе однозначно определяют положение механической системы, называются обобщенными координатами и обозначаются

Принцип возможных перемещений. Исследуем общие условия равновесия механической системы. Под равновесием понимается такое состояние механической системы, при котором все ее точки под действием приложенных сил остаются в покое относительно рассматриваемой системы отсчета. Равновесие является частным случаем движения механической системы, когда скорости всех ее точек равны нулю.
В основе аналитической статики лежит принцип возможных перемещений: для равновесия механической системы с идеальными удерживающими стационарными связями необходимо и достаточно, чтобы суммарная элементарная работа всех действующих на нее активных сил на любом возможном перемещении системы была равна нулю:
Это уравнение называется общим уравнением статики.
Когда система из п материальных точек
находится в равновесии при действии активных сил
и реакций
идеальных удерживающих стационарных связей, для любой точки
можно записать уравнение равновесия:

Определив работу заданных сил на возможном перемещении
всех точек
и просуммировав выражения
почленно, найдем для всей системы:
в координатной форме:
Общее уравнение статики в обобщенных координатах записывается в виде
где Q, — обобщенная сила, соответствующая обобщенной координате
s — число степеней свободы системы.

3. Дифференциальное уравнение движения механической системы в обобщенных координатах (уравнения Лагранжа II рода).
Предположим, что механическая система из п материальных точек имеет S степеней свободы. В случае голономных нестационарных связей радиус-вектор
любой точки
этой системы является функцией обобщенных координат
и времени t:
Обобщенные координаты системы являются функциями времени.
Поэтому радиус-вектор
является сложной функцией времени и вектор скорости точки
определяется по правилу дифференцирования сложной функции:
или

Производные от обобщенных координат по времени
называются обобщенными скоростями.
Частная производная от
по какой-либо обобщенной скорости
равна коэффициенту при
в правой части этого выражения, т.е. равна частной производной от
по координате
Кинетическая энергия механической системы, как известно, определяется по формуле:
Вектор скорости точки
в случае голономных нестационарных связей является функцией обобщенных координат, содержащихся в выражениях
обобщенных скоростей и времени.

Поэтому кинетическая энергия механической системы является функцией тех же переменных:
Найдем частные производные от кинетической энергии по обобщенной координате
и обобщенной скорости
дифференцируя выражение как сложную функцию:
Преобразуем последнее выражение на основании равенства

Продифференцируем это выражение по времени:
Рассмотрим две суммы, входящие в правую часть полученного равенства, учитывая, что для несвободной материальной точки
1. С помощью равенства, определяющего обобщенную силу, находим:
2. Для установления значения второй суммы рассмотрим выражение

Частная производная
является функцией тех же переменных, от которых зависит
радиус-вектор точки
Дифференцируем
как сложную функцию времени:
Найдем частную производную
дифференцируя по
выражение (1):
Подставляем найденные значения обеих сумм в равенство (3.6) и рассматриваем механическую систему со стационарными идеальными связями, для которых