Содержание
- 2. ПРОЦЕНТЫ В МАТЕМАТИКЕ. 1 категория: - простые: а. нахождение процента от данного числа; б. нахождение числа
- 3. Сложные задачи Задача: При двух последовательных одинаковых процентных повышениях зарплаты сумма в 100 рублей обратилась в
- 4. Задачи на сплавы и смеси. Имеется кусок сплава меди с оловом массой 12 кг, содержащий 45%
- 5. Экономические задачи. Известно, что вклад за год хранения возрастает на определенный процент. В начале года 5/6
- 6. Кредиты в “Эльдорадо”. 1.Банк «Русский стандарт» Предоставляет несколько вариантов кредитования: Кредит на встраиваемую технику: - первоначальный
- 8. Скачать презентацию
Слайд 2ПРОЦЕНТЫ В МАТЕМАТИКЕ.
1 категория:
- простые:
а. нахождение процента от данного
ПРОЦЕНТЫ В МАТЕМАТИКЕ.
1 категория:
- простые:
а. нахождение процента от данного

числа;
б. нахождение числа по его процентам;
в. нахождение процентного отношения двух чисел;
- сложные;
2 категория:
- задачи на сплавы и смеси;
- экономические задачи;
- процентное содержание (концентрация);
б. нахождение числа по его процентам;
в. нахождение процентного отношения двух чисел;
- сложные;
2 категория:
- задачи на сплавы и смеси;
- экономические задачи;
- процентное содержание (концентрация);
Слайд 3Сложные задачи
Задача:
При двух последовательных одинаковых процентных повышениях зарплаты сумма в 100
Сложные задачи
Задача:
При двух последовательных одинаковых процентных повышениях зарплаты сумма в 100

рублей обратилась в 125,44 рубля. Определите, на сколько процентов повышалась зарплата.
Решение:
Из второй формулы сложного процента при А=125,44, А=100, n=2, имеем
(1+ p / 100)ⁿ = A / A , (1+p/100)² = 1,2544 ,
1+ p/ 50 + p² /10000 = 1,2544,
p² + 200p 2544 = 0,
p =100 ± √10000 + 2544 = -100 ± 112,
p = 12, p = -212.
Ответ: 12%.
Решение:
Из второй формулы сложного процента при А=125,44, А=100, n=2, имеем
(1+ p / 100)ⁿ = A / A , (1+p/100)² = 1,2544 ,
1+ p/ 50 + p² /10000 = 1,2544,
p² + 200p 2544 = 0,
p =100 ± √10000 + 2544 = -100 ± 112,
p = 12, p = -212.
Ответ: 12%.
Слайд 4Задачи на сплавы и смеси.
Имеется кусок сплава меди с оловом массой
Задачи на сплавы и смеси.
Имеется кусок сплава меди с оловом массой

12 кг, содержащий 45% меди. Сколько чистого олова надо прибавить к этому сплаву, чтобы получившийся новый сплав содержал 40% меди?
Решение:
Сплав состоит из меди и олова. Проследим за содержанием одного из этих веществ, например, олово в первоначальном сплаве и в полученном.
В 12 кг сплава было 45% меди, а олова в нем было 55%, т.е.
12 * 55% / 100% кг олова. Пусть к первоначальному сплаву добавили x кг олова.
Тогда получилось (12+ x) кг нового сплава, в котором олово стало 60%, т.е. 60%(12+x) / 100% кг.
Таким образом, получается следующее уравнение:
55% * 12 / 100% + x = 60% (12+ x) / 100%.
Решив это уравнение, найдем, что x = 1,5. по смыслу задачи x > 0. Найденное значение x условию удовлетворяет. Итак, к первоначальному сплаву следует добавить 1,5 кг олова.
Ответ: 1,5 кг олова.
Решение:
Сплав состоит из меди и олова. Проследим за содержанием одного из этих веществ, например, олово в первоначальном сплаве и в полученном.
В 12 кг сплава было 45% меди, а олова в нем было 55%, т.е.
12 * 55% / 100% кг олова. Пусть к первоначальному сплаву добавили x кг олова.
Тогда получилось (12+ x) кг нового сплава, в котором олово стало 60%, т.е. 60%(12+x) / 100% кг.
Таким образом, получается следующее уравнение:
55% * 12 / 100% + x = 60% (12+ x) / 100%.
Решив это уравнение, найдем, что x = 1,5. по смыслу задачи x > 0. Найденное значение x условию удовлетворяет. Итак, к первоначальному сплаву следует добавить 1,5 кг олова.
Ответ: 1,5 кг олова.
Слайд 5Экономические задачи.
Известно, что вклад за год хранения возрастает на определенный процент.
Экономические задачи.
Известно, что вклад за год хранения возрастает на определенный процент.

В начале года 5/6 некоторой суммы денег положили в первый банк, а оставшуюся часть – во второй. К концу первого года хранения общая сумма с накоплениями составила 670 единиц, к концу второго года – 749 единиц. Если бы первоначально 5/6 исходной суммы положили бы во второй банк, а 1/6 – в первый, то к концу первого года общая сумма составила бы 710 единиц. Определить общую сумму по истечению двух лет, если бы исходная сумма была положена в первый банк.
Решение:
Пусть x, y – проценты, выплачиваемые соответственно первым и вторым банками, Z – исходная сумма. В этом случае искомая общая сумма составила бы Z(1+x). По условию
(5/6)Z * (1+x) + (Z/6) * (1+y) = 670, (1)
(5/6)Z * (1+x) + (Z/6) * (1+y) = 749, (2)
(1/6)Z * (1+x) + (5/6)Z * (1+y)= 710. (3)
Складывая (1) с (3), имеем:
Z(1+x) + Z(1+y) = 1380 ↔ (1+x) + (1+y) = 1380/Z.
Вычитая из (1) (3), имеем
(4/6)Z * (1+x) - (4/6)Z * (1+x) = - 40 ↔ (1+x) - (1+y) = - 60/Z.
Складывая и вычитая полученные уравнения, имеем:
2(1+x) = 1320/Z,
2(1+y) = 1440/Z,
Откуда имеем
(1+x)/(1+y) = 11/12
И
(1+y)² = 144/121 * (1+x)².
Подставляя значение (1+y)² в уравнение (2) , имеем:
(5/6)Z * (1+x)² + Z/6(1+x)² * 144/121 = 749 ↔
↔ Z(1+x)² * (5/6 + 144/6 * 121) = 749 ↔ Z(1+x)² = 726.
Ответ: 726.
Решение:
Пусть x, y – проценты, выплачиваемые соответственно первым и вторым банками, Z – исходная сумма. В этом случае искомая общая сумма составила бы Z(1+x). По условию
(5/6)Z * (1+x) + (Z/6) * (1+y) = 670, (1)
(5/6)Z * (1+x) + (Z/6) * (1+y) = 749, (2)
(1/6)Z * (1+x) + (5/6)Z * (1+y)= 710. (3)
Складывая (1) с (3), имеем:
Z(1+x) + Z(1+y) = 1380 ↔ (1+x) + (1+y) = 1380/Z.
Вычитая из (1) (3), имеем
(4/6)Z * (1+x) - (4/6)Z * (1+x) = - 40 ↔ (1+x) - (1+y) = - 60/Z.
Складывая и вычитая полученные уравнения, имеем:
2(1+x) = 1320/Z,
2(1+y) = 1440/Z,
Откуда имеем
(1+x)/(1+y) = 11/12
И
(1+y)² = 144/121 * (1+x)².
Подставляя значение (1+y)² в уравнение (2) , имеем:
(5/6)Z * (1+x)² + Z/6(1+x)² * 144/121 = 749 ↔
↔ Z(1+x)² * (5/6 + 144/6 * 121) = 749 ↔ Z(1+x)² = 726.
Ответ: 726.
Слайд 6Кредиты в “Эльдорадо”.
1.Банк «Русский стандарт»
Предоставляет несколько вариантов кредитования:
Кредит на встраиваемую технику:
- первоначальный
Кредиты в “Эльдорадо”.
1.Банк «Русский стандарт»
Предоставляет несколько вариантов кредитования:
Кредит на встраиваемую технику:
- первоначальный

взнос- 10% от стоимости товара
- срок кредита- 6,10,12,24,36,48 месяцев
- процентная ставка- 13% годовых
- размер кредита: 25000-450000 рублей
- комиссия за расчетно-кассовое обслуживание- 1% ежемесячно от
суммы кредита
- кредит предоставляется на всю встраиваемую технику
10-10-10:
- первоначальный взнос- 10% от стоимости товара
- срок кредита- 10 месяцев
- ежемесячный платеж-10%
- выдается на все группы товаров, кроме мобильных телефонов.
Обычный:
- первоначальный взнос- 10% от стоимости товара
- срок кредита- 6,12,18,24 месяцев
- процентная ставка- 19% годовых
- комиссия за расчетно-кассовое обслуживание- 1,99% ежемесячно от суммы кредита
- выдается на все товары, кроме мобильных телефонов
0% первый взнос:
- первоначальный взнос- 0%
- срок кредита- 6,12 месяцев
- процентная ставка- 29% годовых
- комиссия за расчетно-кассовое обслуживание-1,9% ежемесячно от суммы товара
- предоставляется на все группы товаров, кроме мобильных телефонов
- срок кредита- 6,10,12,24,36,48 месяцев
- процентная ставка- 13% годовых
- размер кредита: 25000-450000 рублей
- комиссия за расчетно-кассовое обслуживание- 1% ежемесячно от
суммы кредита
- кредит предоставляется на всю встраиваемую технику
10-10-10:
- первоначальный взнос- 10% от стоимости товара
- срок кредита- 10 месяцев
- ежемесячный платеж-10%
- выдается на все группы товаров, кроме мобильных телефонов.
Обычный:
- первоначальный взнос- 10% от стоимости товара
- срок кредита- 6,12,18,24 месяцев
- процентная ставка- 19% годовых
- комиссия за расчетно-кассовое обслуживание- 1,99% ежемесячно от суммы кредита
- выдается на все товары, кроме мобильных телефонов
0% первый взнос:
- первоначальный взнос- 0%
- срок кредита- 6,12 месяцев
- процентная ставка- 29% годовых
- комиссия за расчетно-кассовое обслуживание-1,9% ежемесячно от суммы товара
- предоставляется на все группы товаров, кроме мобильных телефонов
 Живая и неживая природа.
Живая и неживая природа. Занятость и безработица
Занятость и безработица Ортологическая разминка
Ортологическая разминка Стратегический анализ внешней среды организации
Стратегический анализ внешней среды организации Салонные женские стрижки
Салонные женские стрижки Пермский филиал ГУ ВШЭ Архипов Валерий Михайлович, зам. директора ПФ ГУ-ВШЭ, доцент каф.фин.менеджмента ПФ ГУ-ВШЭ. Ведерников Серге
Пермский филиал ГУ ВШЭ Архипов Валерий Михайлович, зам. директора ПФ ГУ-ВШЭ, доцент каф.фин.менеджмента ПФ ГУ-ВШЭ. Ведерников Серге Фотоэффект (11 класс)
Фотоэффект (11 класс) Что такое мастер-класс?
Что такое мастер-класс? ВЫСТУПЛЕНИЕ РУКОВОДИТЕЛЯ ГМО Белковой Елены Александровны
ВЫСТУПЛЕНИЕ РУКОВОДИТЕЛЯ ГМО Белковой Елены Александровны Выбор и обоснование выбора материала для ________________. Образец презентации по материаловедению
Выбор и обоснование выбора материала для ________________. Образец презентации по материаловедению Оценка и развитие бизнеса
Оценка и развитие бизнеса Ambient Media Что это такое? Что это такое? Ambient против классик и Ambient против классик и Эффективност ь Эффективност ь For ex. For ex. Вывод ы Вывод
Ambient Media Что это такое? Что это такое? Ambient против классик и Ambient против классик и Эффективност ь Эффективност ь For ex. For ex. Вывод ы Вывод Оценка движимого имущества. Практика решения задач
Оценка движимого имущества. Практика решения задач Разделы информатики, используемые в олимпиадных задачах
Разделы информатики, используемые в олимпиадных задачах РАЗВИТИЕ ТЕХНОЛОГИЙ ПРОВЕДЕНИЯ МЕЖРЕГИОНАЛЬНЫХ СДЕЛОК
РАЗВИТИЕ ТЕХНОЛОГИЙ ПРОВЕДЕНИЯ МЕЖРЕГИОНАЛЬНЫХ СДЕЛОК В объятьях двух морей новый
В объятьях двух морей новый Итоги 2009 – 2010 учебного года в 1 – 4 классахПедсовет 30.08 .2010г.
Итоги 2009 – 2010 учебного года в 1 – 4 классахПедсовет 30.08 .2010г.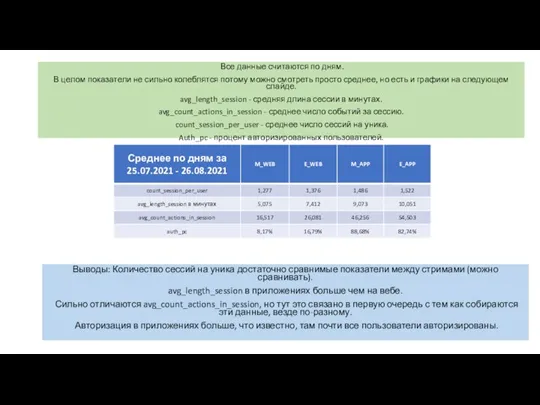 Количество сессий на уника
Количество сессий на уника Сказка о стране чисел
Сказка о стране чисел Актуальные проблемы литературы ХХ века и современной литературы
Актуальные проблемы литературы ХХ века и современной литературы Брейн-ринг Волшебные сказки
Брейн-ринг Волшебные сказки Стили в архитектуре
Стили в архитектуре O
O Мисс Филология
Мисс Филология Презентація Івкової Ольги ФГН-1,філологія, група 2
Презентація Івкової Ольги ФГН-1,філологія, група 2 Humor in advertising
Humor in advertising Презентация на тему Что мы знаем о тексте 5 класс
Презентация на тему Что мы знаем о тексте 5 класс Приготовление рабочих растворов
Приготовление рабочих растворов