Производная

1. Выражение вида Δf появилось уже в конце 17 в. и означает «приращение».
2. Термин производная ввел в 1797г. Ж. Лагранж
3.И. Ньютон называл производную функцию
флюксией , а саму функцию – флюентой.
4.Раздел математики, в котором изучаются производные и их применения к исследованию функций , называется дифференциальным исчислением.
5.Дифференциальное исчисление создано Ньютоном и Лейбницем
в конце 17 столетия.
Историческая страничка
1736-1813гг.
1643-1727гг.
1646-1716гг.

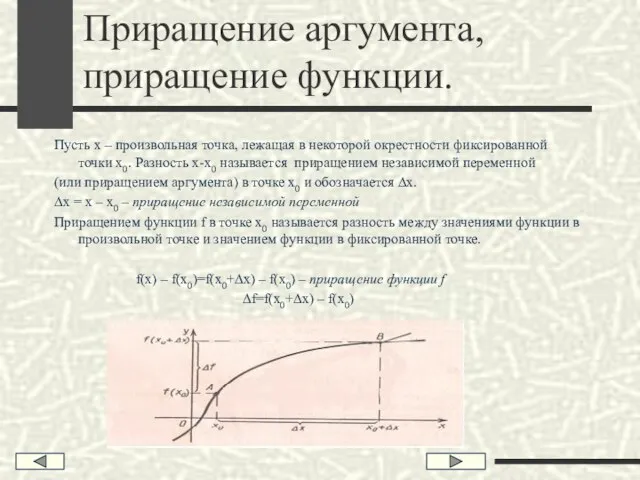
Приращение аргумента,
приращение функции.
Пусть х – произвольная точка, лежащая в некоторой окрестности фиксированной точки х0. Разность х-х0 называется приращением независимой переменной
(или приращением аргумента) в точке х0 и обозначается ∆х.
∆х = х – х0 – приращение независимой переменной
Приращением функции f в точке x0 называется разность между значениями функции в произвольной точке и значением функции в фиксированной точке.
f(х) – f(х0)=f(х0+∆х) – f(х0) – приращение функции f
∆f=f(х0+∆х) – f(х0)

Определение производной.
Отношение приращения функции к приращению аргумента называется
разностным отношением
Производной функции f в точке х0 называется число к которому стремиться разностное отношение: при ∆х 0.
Задача. Найти производную функции f(x)=x2, используя определение.
Решение. 1) f(x0)=x02 - значение функции в фиксированной точке.
f(x0+∆x)=(x0+∆x)2-значение функции в произвольной точке.
2) Найдём приращение функции:
∆f=f(x0+∆x)-f(x0)=(x0+∆x)2-x02 =x02+2x0∆x+∆x2-x02=2x0∆x+∆x2.
3)Найдем разностное отношение:
4)При ∆x 0 2х0+∆х 2х0, значит (х02)'=2х0.
5)Для любого х: (х2)'=2х.

Основные формулы дифференцирования.
(xn)'=nxn-1 – производная степенной функции
Частные случаи:
2)(kx+b)'=k-производная линейной функции
3)с'=0-производная постоянной
4)Производные тригонометрических функций:
a)(sinx)'=cosx b)(cosx)'=-sinx
c)(tgx)'=1/cos2x d)(ctgx)'=-1/sin2x

Основные правила дифференцирования
Если функции u и v дифференцируемы в точке х0, то справедливы следующие правила:
1)(u+v)'=u'+v'
2)(uv)'=u'v+uv'
3)(cu)'=cu'
4)(u/v)'=u'v-uv'/v2,v не равно нул'ю
5) h' (x0)=g' (f(x0))f '(x0)

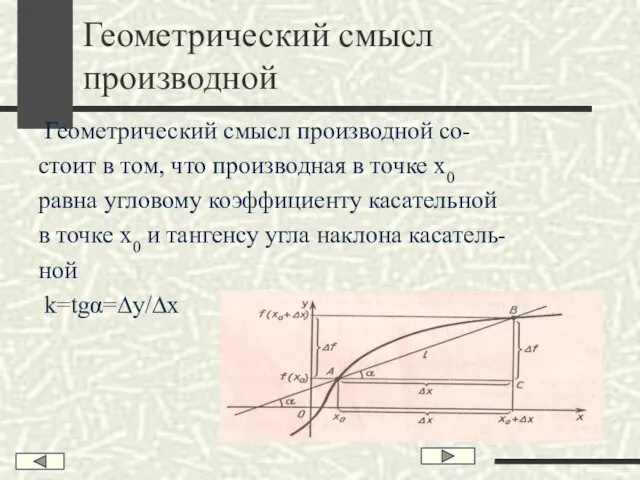
Геометрический смысл производной
Геометрический смысл производной со-
стоит в том, что производная в точке х0
равна угловому коэффициенту касательной
в точке х0 и тангенсу угла наклона касатель-
ной
k=tgα=∆y/∆x

Механический смысл производной
Механический смысл производной состо-
ит в том, что производная пути по време-
ни равна мгновенной скорости в момент
времени t0:
S'(t0)=V(t0).

Образцы решения задач.
Решая примеры, проговаривай вслух.
Помни: «Мысль рождается с собственной речи!»

Продифференцируй функцию:
1)f(x)=4/(9+7x)5 2)g(x)=x2sin2x
3)y=1/cos2x 4)u(x)=x2/x3-1
Найди угловой коэффициент касательной к графику функции у=15х+cosx в точке с абсциссой х0=-π.
Найди точки, в которых f‘(x)=0, f(x)'>0,если f(x)=2x+cos(4x- π).
Задай формулой хотя бы одну функцию, производная которой равна:
а) 4x+5
б) 6x2-sinx
Проверь свои знания!

Подготовься к ЕГЭ.
Найди производную функций:
у=(7х+3)3 у=х2/х+3
у=3х4+sinx+5 y= tgx+3sin2x
Найди тангенс угла наклона касательной, проведённой к графику функции у=-4/х в точке с абсциссой равной -3.
Найди значение производной функции у=хcosх
в точке х0=π.
Решить уравнение f'(x)=0,если f(x)=x3-2x2