Производная

Физический смысл производной
Содержание
Основные формулы дифференцирования
Производная элементарных функций
Геометрический смысл
Правила дифференцирования
Производная частных функций
Понятие производной

Непрерывность
Исследование функции с помощью производной
Задачи на нахождение наибольшего и
Наименьшего значения функции
Практическая часть

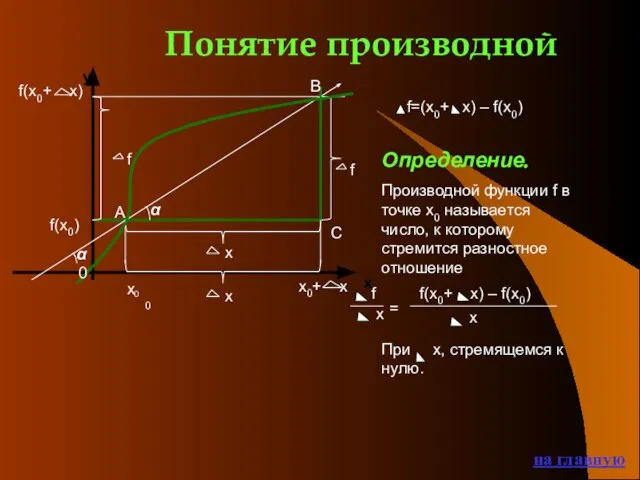
Понятие производной
на главную
f=(x0+ x) – f(x0)
Определение.
Производной функции f в точке х0 называется число, к которому стремится разностное отношение
При х, стремящемся к нулю.

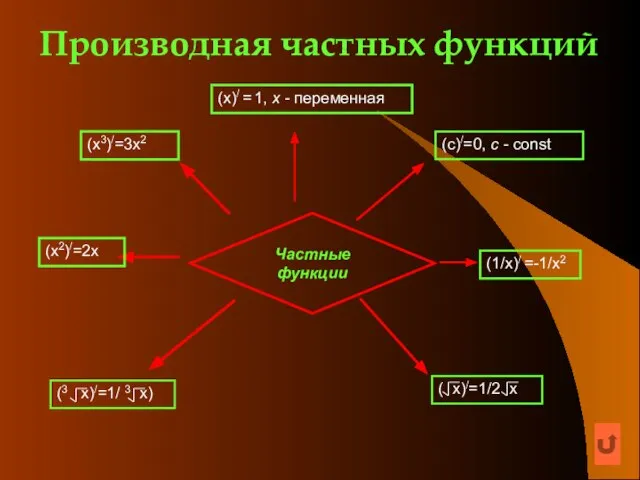
Производная частных функций

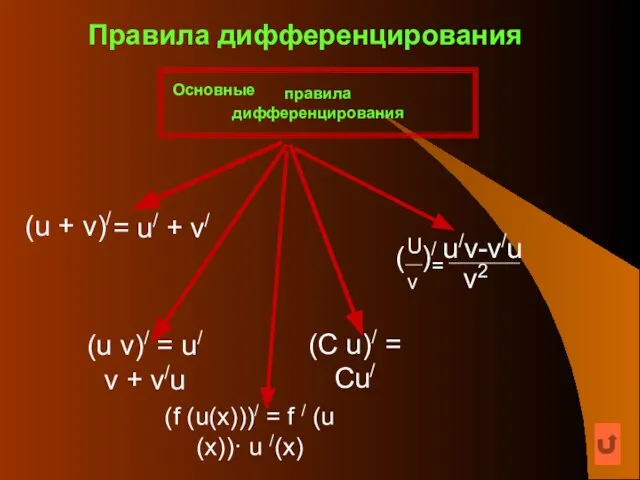
Правила дифференцирования
(u v)/ = u/ v + v/u
(C u)/ = Cu/
(f (u(х)))/ = f / (u (х))· u /(х)

Основные формулы дифференцирования
(Sinх)´ = cosх
( Cosх)´ = -Sinх
(lnх)' = 1/х
х>0
(log a)' = 1/(х ln а)
(eх)' = eх
(ах)' = ах lnа
(kх + b )' = k
(х р)´ = р х р -1
(ln (kх + b) )' = k/ kх + b
(log a)' = 1/х ln а
(lg)/ = 1/х · lg e
(ctgх)/ = - 1/sin2 х
(tgх)/ = 1/cos2 х
(kх + b )' = k

Геометрический смысл производной
Пусть задана функция y = f(х), которая имеет производную в точке х = а. Через
точку (а; f(a)), проведена касательная к графику функции y = f(х). Угловой
Коэффициент или тангенс угла наклона этой касательной будет равен
производной функции y = f(х) в точке х = а, то есть k = tg α= f /(a) .
Y= f (a) + f /(a) (х-a)
Уравнение касательной

Непрерывность
Функция y = f(x) называется непрерывной на промежутке, если она определена на этом промежутке и непрерывна в каждой точке промежутка.
Геометрическая непрерывность функции на промежутке означает, что график этой функции на данном промежутке изображен сплошной линией без скачков и разрывов. При этом малому изменению аргумента соответствует малое изменение функции.
Если при x = a функция y = f(x) существует в окрестности этой точки, но в самой точке x = a не выполняется условие непрерывности, говорят, что точка x = a есть точка разрыва функции. В самой точке x = a функция может существовать, а может и не существовать.
на главную

Пусть точка движется по некоторой прямой линии, так что ее положение меняется с течением времени. Рассмотрим эту прямую как числовую ось, тогда положение точки определяется её координатой, и с течением времени эта координата меняется, являясь тем самым функцией от времени. Уравнением движения называется запись у = f (t), показывающая, каким образом меняется координата с течением времени.
Скорость движения с уравнением у = f (t) в момент времени t равна значению производной f '(t) в этот момент времени. В этом состоит физический смысл производной.
Скорость движения при неравномерном движении изменяется с течением времени. Скорость изменения скорости называется ускорением,
То есть f ' '(t). В этом состоит физический смысл второй производной.
Физический смысл производной

Определение 1. Пусть функция y = f(x) определена на отрезке[a; b]. Говорят, что функция имеет максимум в точке x0 [a; b], если существует окрестность точки x0, целиком содержащаяся в [a; b] и такая, что для любого x, принадлежащего этой окрестности, выполняется неравенство f(x) < f(x0).
Под окрестностью точки x0 понимают интервал длины 2e с центром в точке x0, т. е. (x0 – e ; x0 + e), где e – произвольное положительное число.
Определение 2. Пусть функция y = f (x) определена на отрезке [a; b]. Говорят, что функция имеет минимум в точке x0 [a; b], если существует окрестность точки x0, целиком содержащаяся в [a; b] и такая, что для любого x, принадлежащего этой окрестности, выполняется неравенство f (x) > f(x0).

Максимумы и минимумы функции не являются обязательно наибольшими и наименьшими значениями этой функции во всей области определения. Например, функция y = f (x) определена на отрезке [a; b], имеет четыре экстремума: два минимума (x = C1 и x = C3) и два максимума (x = C2 и x = C4). Вместе с тем, функция достигает наибольшего значения при x = a и наименьшего при x = b.
Признак максимума функции:
Если функция непрерывна в точке x0
и ее производная, переходя через нее,
меняет знак с плюса на минус,
то x0 есть точка максимума.
Признак минимума функции:
Если функция непрерывна в точке x0
и ее производная, переходя через нее,
меняет знак с минуса на плюс, то x0 есть
Точка минимума.

Схема исследования:
Область определения.
Чётность.
Периодичность.
Критические точки.
Значение функции в критических точках.
Промежутки возрастания и убывания.
Экстремумы.
Наибольшее и наименьшее значение функции.
Дополнительные точки.
Пример: исследовать функцию у = - х3 + 3х - 2 и построить её график
Решение:
Область определения: DУ = (- ∞; +∞ ).
Функция не является ни чётной, ни нечётной.
Функция не является периодической.
Производная: у‘ = 0 при х = 1 и х = -1.
6. У ‘(1) = 0; у(-1) = - 4.
7. у‘ < 0 при х є ( - ∞ ; -1), следовательно, на промежутке ( - ∞ ; -1) функция убывает;
у‘ > 0 при х є ( - 1; 1) функция возрастает;
у‘ < 0 при х є ( 1; +∞ ), следовательно, на промежутке ( 1; +∞) функция убывает.
Так как в точка х = -1 и х = 1 функция непрерывна, то эти точки присоединим к промежуткам
убывания и промежутку возрастания.
(- ∞ ; - 1]; [ 1; + ∞ ) – промежутки убывания. [-1;1] – промежуток возрастания.
Исследование функции с помощью производной

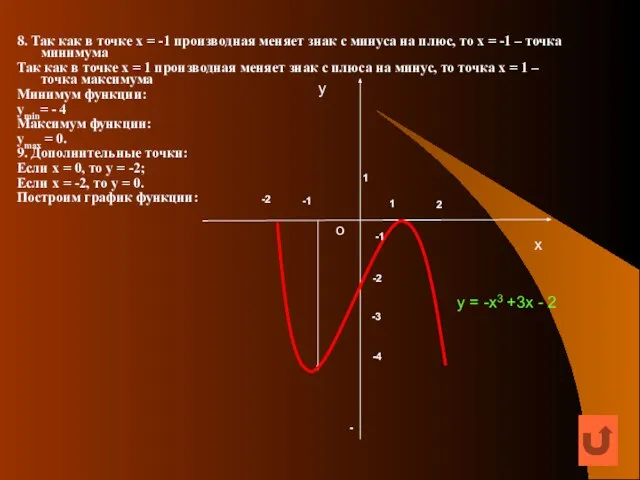
8. Так как в точке х = -1 производная меняет знак с минуса на плюс, то х = -1 – точка минимума
Так как в точке х = 1 производная меняет знак с плюса на минус, то точка х = 1 – точка максимума
Минимум функции:
ymin= - 4
Максимум функции:
ymax = 0.
9. Дополнительные точки:
Если х = 0, то y = -2;
Если х = -2, то y = 0.
Построим график функции:

Задачи на нахождение наименьшего
и наибольшего значения функции.
Пусть функция у = f (х), х є [а; b], непрерывна на отрезке [а; b], дифференцируема во всех точках этого отрезка и имеет конечное число критических точек на этом отрезке.
Чтобы найти наибольшее и наименьшее значение функции у = f (х), на отрезке [а; b], необходимо:
Найти критические точки;
Вычислить значение функции на концах отрезка и в критических точках;
Выбрать из найденных значений наибольшее и наименьшее.
если функция у = f (х) возрастает на отрезке [а; b], то f (a) – наименьшее значение, f (b) – наибольшее значение функции на этом отрезке.
если функция у = f (х) убывает на отрезке [а; b], то f (а) – наибольшее значение, f (b) - наименьшее значение функции на этом отрезке.

Практическая часть
Найти наибольшее и наименьшее значение функции на отрезке:
Решение: данная функция непрерывна и дифференцируема в каждой точке отрезка
[ -1; 2].
Найдём производную: у/ = х2 – 4х + 3.
Найдём критические точки: у/ = 0 при х = 1 и х = 3, 3€ [ -1; 2].
Найдём значение функции в точке х = 1 и на концах отрезка [ -1; 2]:
У (1) = 13 /3 – 2 · 12 + 3 · 1 + 1 = 1/3 – 2 + 3 + 1 = 2
У(-1)=(-1)3/3 - 2· (-1)2 + 3· (-1) + 1= - 4
У(2)= 23/3 – 2 · 22 + 3 · 2 + 1 = 1
Ответ: max у(х) = 2 ; min у(х) = - 4 .
[-1;2] [-1;2]

Составьте уравнение касательной к параболе у =2 х2 – 12х + 20 в точке с абсциссой х = 4.
Решение:
уравнение касательной функции у = f (х) в точке х = a: у = f (а) +
f / (а)( х – а)
Найдём производную функции
f (
2 х2 – 12х + 20:
Х) =
f/ (х) = 4х – 12.
Найдём значение производной и функции при х = 4:
f/ (4) = 4· 4 – 12 = 4
f (х) = 2 · 42 – 12 · 4 + 20 = 4.
Составим уравнение касательной:
У = 4 + 4 (х – 4);
У = 4 + 4х – 16;
У = 4х – 12
У = 4х – 12 - уравнение касательной к параболе у =2 х2 – 12х + 20 в точке
с абсциссой х = 4.
Ответ: У = 4х – 12.

Найти промежутки возрастания и убывания, точки максимума и точки минимума функции, максимумы и минимумы функции:
у = 2х2 + 4х + 1.
Решение: Найдём производную данной функции: у/ = 4х + 4.
Так как у/ > 0 на ( - 1; + ∞), значит, на этом интервале функция возрастает.
Так как у/ < 0 на ( - ∞; - 1), значит, на этом интервале функция убывает.
Так как в точке х = - 1 функция у = 2х2 + 4х + 1 непрерывна, то эту точку присоединим к промежутку возрастания и промежутку убывания, то есть на промежутке [ - 1; + ∞), функция возрастает, на промежутке ( - ∞; - 1],
функция убывает;
Так как в точке х = - 1 производная меняет знак с минуса на плюс, то х = - 1 является точкой минимума.
Найдём минимум функции:
уmin = 2*( - 1)2 + 4 (- 1) + 1 = - 1.
Ответ: на [ - 1; + ∞), функция возрастает, на промежутке ( - ∞; - 1],
функция убывает; хmin = - 1; уmin = - 1.

Найти координаты точки, в которой касательная к параболе у =
3/2 х2 - 4х + 5 образует угол 135o с осью Ох.
Решение:
Тангенс угла наклона равен производной функции в точке касания, то есть t g 135o =
f /(х), t g 135o = -1
f /(х) = (3/2 х2 - 4х + 5 )/ = 3х – 4, 3х – 4 = - 1; 3х = 3; х = 1.
Значит, 1 – абсцисса точки касания. Найдём ординату этой точки:
f (1) = 3/2 · 12 – 4 · 1 + 5 = 3/2 – 4 + 5 = 2,5
(1; 2,5) – координаты точки касания.
Ответ: (1; 2,5).

Материальная точка движется прямолинейно по закону х (t) = 1/3 t3 – ½ t2 + 2. Выведите формулу для вычисления скорости в любой момент времени и найдите скорость в момент t = 5 с. (Путь – в метрах).
Решение: Скорость движения с уравнением х (t) = 1/3 t3 – ½ t2 + 2 в момент времени t равна значению производной х/ (t) в этот момент времени.
Поэтому:
V = х/ (t) = t2 - t
Найдём скорость в момент времени t = 5;
V (5) = 52 – 5 = 25 – 5 = 20 (м/с).
Ответ: V = 20 (м/с).