Пропорция

ПРОПОРЦИЯ
Ничто не нравится, кроме красоты,
в красоте – ничто, кроме форм,
в формах – ничто, кроме пропорций,
в пропорциях – ничто, кроме числа.
(Аврелий Августин)
354-430г.г.

Из истории изучения пропорции
Слово «пропорция»
ввел в употребление Цицерон в 1 веке до н.э., который буквально означал аналогия, соотношение.

Начало изучения пропорции
Пропорции начали изучать еще в древности.
В 4 веке до н.э. древнегреческий математик Евдокс
дал определение пропорции, составленной из величин любой природы.

ПРОПОРЦИЯ
определение
Пропорция - равенство между отношениями
четырёх величин А, В, С, D: A : B = C : D,
где A и D – это крайние члены пропорции,
а B и C – средние члены пропорции

Основное свойство пропорции
Произведение средних членов пропорции равно произведению крайних.
A • D = B • C
2 : 5 = 4 : 10
2 •10 = 5 • 4
20 = 20

Как найти неизвестный член пропорции
Решить уравнение
Х : 5= 4 :1 0 Х = 5 • 4 : 10
Х = 2
Ответ: 2

Прямая пропорциональность Пример решения задачи с помощью пропорции
Задача. Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?
Решение
Массы семени и масла находятся в прямой пропорциональной зависимости, значит можно составить пропорцию:
21 : 7 = 5,1 : Х
Х = 7 • 5,1 : 21
Х = 1,7
Ответ: Из 7 кг хлопкового семени получится 1,7 кг масла.

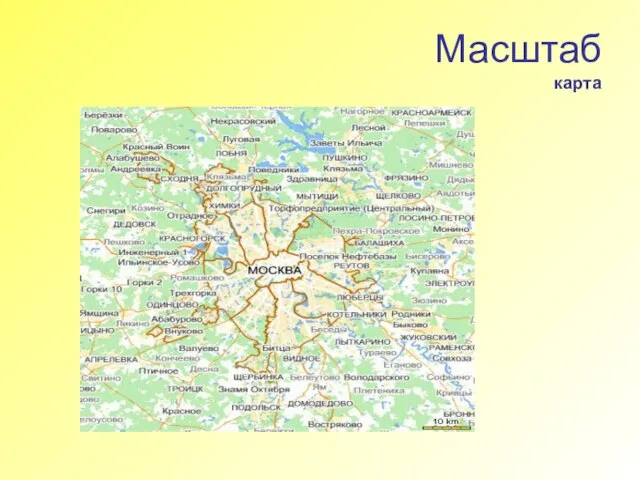
Масштаб
карта

Масштаб
пример решения задачи
Задача. Расстояние между станциями Луганск и Россошь равна 185 км. Какое расстояние между этими городами на карте, если масштаб 1:5000000?
Решение
1 : Х = 5 000 000 : 18 500 000
Х = 18 500 000 : 5 000 000
Х = 3,7
Ответ: расстояние между городами Луганск и Россошь на карте равно
3,7 см.

Обратная пропорциональность
Пример решения задачи с помощью пропорции
Задача. Для строительства стадиона 5 бульдозеров расчистили площадку за 210 мин. За какое время 7 бульдозеров расчистили бы эту площадку?
Решение.
Количество бульдозеров и время расчистки площадки находятся пропорциональной зависимости, значит можно составить пропорцию: 5 : 7 = Х : 210
Х = 5 • 210 :7
Х = 150
Ответ: 7 бульдозеров расчистят площадку за 150 мин.

Задача на пропорциональное деление
Задача.
Найти смежные углы, если их величины находятся в отношении 2 :7.
Решение
Пусть 1 часть равна Х0, тогда первый угол равен 2Х0,
второй угол равен 7Х0.
По свойству смежных углов их сумма равна 1800, значит
2Х + 7Х = 180
9Х = 180
Х =20
7 • 200 = 1400
2 • 200 = 400
Ответ: 400; 1400.

Теорема Фалеса
Если параллельные прямые,
пересекающие стороны угла,
отсекают на одной его стороне
равные отрезки,
то они отсекают равные отрезки
и на другой его стороне.
Можно также доказать,
что параллельные прямые,
пересекающие стороны угла,
отсекают от сторон угла
пропорциональные отрезки.

Преобразование подобия
Преобразования, сохраняющие форму фигур, но изменяющие их размеры
называют преобразованием подобия.
Каждую фигуру F преобразование подобия переводит в подобную ей фигуру F', представляющую собой увеличенную или уменьшенную копию первоначальной фигуры.

Преобразование подобия
пример

Коэффициент подобия
Все размеры фигуры F' равны соответствующим размерам фигуры F, умноженным на одно и то же число к – коэффициент подобия.

Примеры подобия фигур
Модель автомашины - это уменьшенная копия оригинала.

Перед тем, как построить какое-то здание сооружают его макет. Макет-это тоже уменьшенная копия оригинала.
Примеры подобия фигур
продолжение

Как получить подобные фигуры
Подобные фигуры можно получить поместив под лампой вырезанную из куска картона фигуру F, плоскость которой параллельна поверхности стола. Тень F', отбрасываемая этой фигурой на стол, будет подобна
фигуре F.

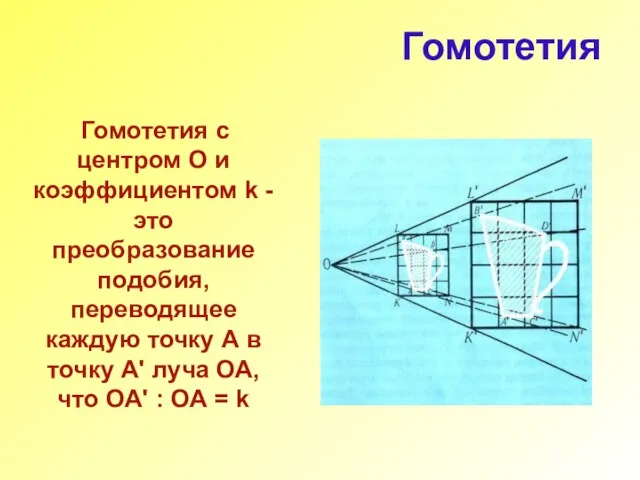
Гомотетия
Гомотетия с центром О и коэффициентом k -это преобразование подобия, переводящее каждую точку А в точку А' луча ОА, что ОА' : ОА = k

Роль пропорции
в искусстве
Пропорция в искусстве определяет соотношение отдельных элементов
и всего художественного произведения
в целом.

Роль пропорции
в архитектуре
В архитектуре пропорции являются
важным и надежным средством для достижения
равновесия
между целым
и его частями.