Разработка и исследование алгоритмов алгебраического криптоанализа

Задача алгебраического криптоанализа
Алгебраические атаки используют внутреннюю структуру шифра, то есть для получения ключа шифрования необходимо представить преобразования шифрования в виде системы многомерных многочленных уравнений и впоследствии решить данную систему.
Несмотря на то, что данный метод может быть применим к некоторому числу алгоритмов шифрования, в данной работе анализ алгебраический методов сфокусирован на применении их к алгоритму шифрования Rijndael, а точнее его упрощенному варианту - BabyRijndael.

Значимость задачи
Большинство современных шифров было создано с учетом традиционных методов криптоанализа, таких как дифференциальный и линейный , поэтому такого рода атаки зачастую не оказывают влияния на их безопасность. Для большинства подобных атак сложность возрастает экспоненциально с ростом числа раундов, при этом данные методы становятся неэффективными.
В отличие от них, алгебраический криптоанализ затрагивает внутреннюю структуру шифров и оказывается более эффективным. Следует отметить возможность улучшения производительности алгебраических алгоритмов криптоанализа путем распараллеливания вычислительных процессов.

Алгоритм одного раунда упрощенного варианта шифра Rijndael
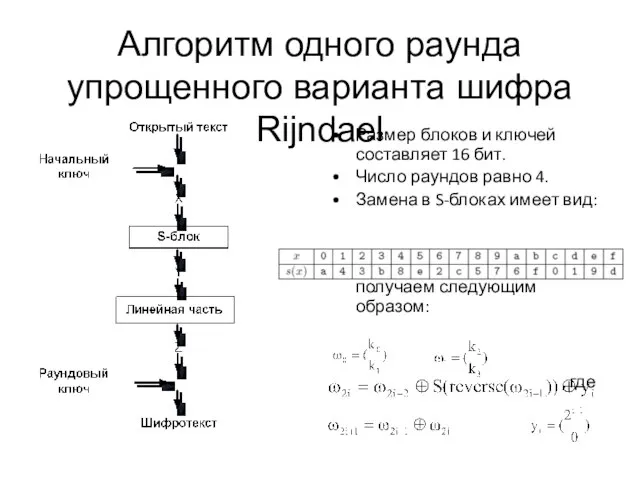
Размер блоков и ключей составляет 16 бит.
Число раундов равно 4.
Замена в S-блоках имеет вид:
Столбцы раундового ключа получаем следующим образом:
, где

Алгоритм шифрования для упрощенной модели Rijndael

Система уравнений S-блоков
Уравнения, описывающие работу S-блоков, имеют вид:
Максимальное число одночленов равно t=( )+2n+1
Для составления уравнений необходимо получить таблицу истинности вида:

Получение системы уравнений
Можно выделить три этапа:
Получение уравнений для S-блоков
Получение дополнительных уравнений, учитывающих алгоритм работы S-блоков
Уменьшение числа переменных

Разработка алгоритма получения
уравнений для S-блоков
Рассматриваем вариантов уравнений и отбираем уравнения, удовлетворяющие таблице истинности.
Из полученных уравнений выбираем уравнения, содержащие только один квадратный элемент (то есть элемент вида xiyj, xixj или yiyj)
Определяем, какие из квадратных элементов не встречаются в данных уравнениях
Находим уравнение, в котором присутствует недостающий квадратный элемент
Производим сложение по модулю 2 данного уравнения с другим уравнением, таким чтобы при сложении произошло обнуление уже встречавшихся квадратных элементов.
Отбрасываем уравнения содержащие два и более квадратных элемента.

Получение дополнительных уравнений, учитывающих алгоритм работы S-блоков
Учитывая, что в S-блоках сначала находится обратный входному значению элемент и лишь потом применяется аффинное преобразование, обозначим его через h, можем получить дополнительные уравнения из выражения: или X*h(Y)=(0,0,0,1).
Таким образом, путем приравнивания каждого бита с левой стороны к биту с правой стороны, получим 4 дополнительных уравнения.

Алгоритм уменьшения числа переменных
Исходя из схемы алгоритма шифрования BabyRijndael и алгоритма выработки ключей, возможно произвести следующие замены:
Входное значение S-блока равно открытый текст XOR начальный ключ.
Выходное значение S-блока равно шифротекст XOR раундовый ключ.
Второй столбец раундового ключа представляет собой сумму по модулю 2 второго столбца начального ключа и первого столбца раундового ключа.

XL атака
XL (eXtended Linearization) метод предложили Николя Куртуа, Александр Климов и Ади Шамир в 2000 году.
Обозначим через D параметр алгоритма XL, причем , где n- число переменных, а m- количество уравнений.
Данный алгоритм базируется на перемножении каждого возможного уравнения 1…m на все возможные значения переменных в степени D-2.

Алгоритм реализации XL метода
Multiply: составление всех произведений вида , где k≤D-2;
Linearize: рассмотрение каждого одночлена хi в степени ≤ D как новой переменной и применение Гауссовского исключения к уравнениям, полученным в пункте 1.
Solve: повторение пункта 2 до тех пор, пока в результате не будет получено по крайней мере одно уравнение с единственной переменной.
Repeat: упростить уравнения и повторить процесс для нахождения значений других переменных.

XSL атака
В 2002 году вместо техники XL был создан алгоритм, использующий преимущества особой структуры уравнений и их разреженность. Эта атака была названа XSL-атака, что расшифровывается как «eXtended Sparse Linearization» или «multiply(X) by Selected monomials and Linearize».
Алгоритм XSL предложен для работы только со специальными типами шифров, для который выполняются условия:
S-блоки должны быть такими, чтобы их можно было описать с помощью сверхопределенной системы квадратных уравнений.
Алгоритм получения ключей должен иметь схожую структуру с алгоритмом зашифрования.

Алгоритм реализации XSL метода
Обработка имеющейся системы уравнений путем выбора конкретного набора одночленов и уравнений, которые будут использоваться в дальнейших этапах алгоритма
Выбор значения параметра Р и умножение выбранных на предыдущем этапе уравнений на результаты произведений (Р-1) выбранных одночленов
При недостаточном числе уравнений применение Т’ метода, в котором некоторые выбранные уравнения умножаются на одиночные переменные. Цель данного метода – создание новых уравнений без получения каких-либо новых одночленов.
Применение линеаризации, путем представления каждого одночлена в виде новой переменной и выполнения Гауссовского исключения.

Оценка сложности атаки для алгоритма шифрования BabyRijndael
Для метода XL сложность Гауссовского преобразования составляет:
, где n - число переменных, m - количество уравнений, ω≤3 - показатель Гауссовского преобразования.
Для XSL атаки сложность составляет
, где t – число одночленов, P – параметр алгоритма XSL атаки, S - число S-блоков, ω - показатель Гауссовского преобразования.