Решение логических задач

Задача №1. В одном королевстве король всякому узнику, приговоренному к смерти, давал последний шанс спастись. Ему предлагалось угадать, в какой из двух комнат находится тигр, а в какой - принцесса. Хотя вполне могло быть, что король в обеих комнатах разместил принцесс или, что хуже, в обеих - тигров. Выбор надо сделать на основании табличек на дверях комнат. Причем узнику известно, что утверждения на табличках одновременно либо истины, либо ложны. Надписи были таковы. Первая комната: «По крайней мере, в одной из этих комнат находится принцесса». Вторая комната: «В другой комнате – тигр». Какую дверь должен выбрать узник?
?

P1 = В первой комнате принцесса.
P2 = Во второй комнате принцесса.
P1 = В первой комнате тигр.
P2 = Во второй комнате тигр.

А = Р1 \/ Р2
В = Р1
А & B \/ A & B = 1

А & B \/ A & B = 1
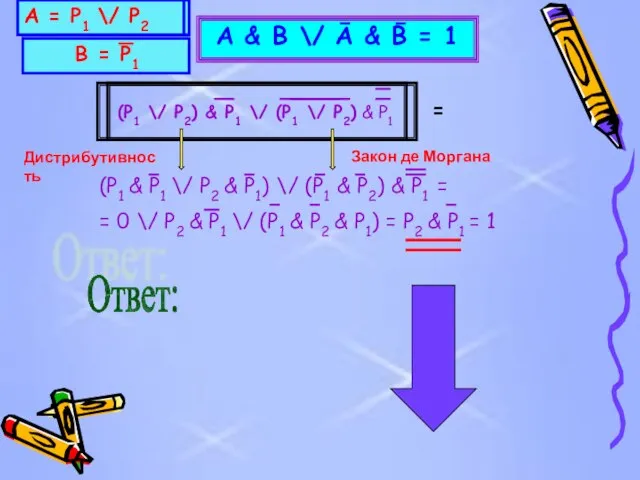
(P1 \/ P2) & P1 \/ (P1 \/ P2) & P1
А = Р1 \/ Р2
В = Р1
=
(P1 & P1 \/ P2 & P1) \/ (P1 & P2) & P1 =
= 0 \/ P2 & P1 \/ (P1 & P2 & P1) = P2 & P1 = 1
Ответ:
А = Р1 \/ Р2
В = Р1
А = Р1 \/ Р2
Дистрибутивность
Закон де Моргана