Содержание
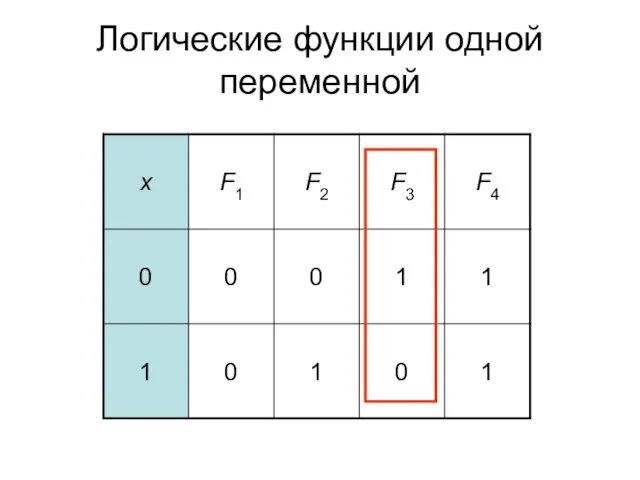
- 2. Логические функции одной переменной
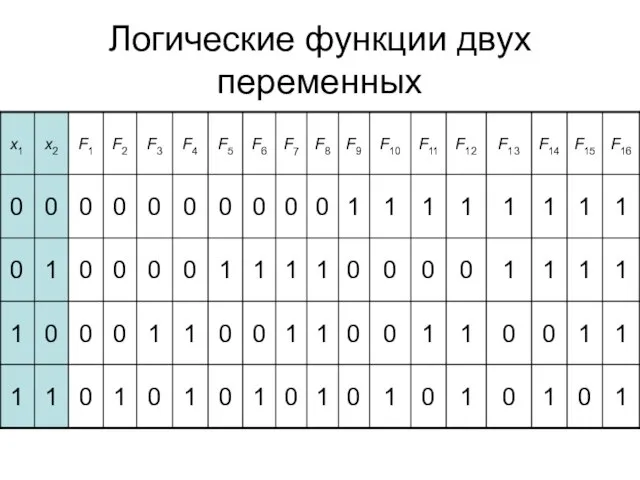
- 3. Логические функции двух переменных
- 4. Логическое умножение Коньюнкция conjunctio – лат. – связываю Соединение двух простых высказываний A и B в
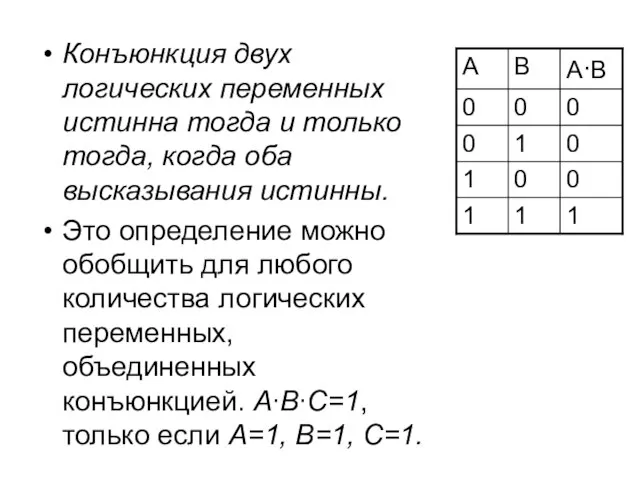
- 5. Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания истинны. Это определение можно
- 6. Свойства конъюнкции
- 7. Логическое сложение Дизъюнкция disjunctio – лат. – различаю Соединение двух простых высказываний A и B в
- 8. Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны. Это определение можно
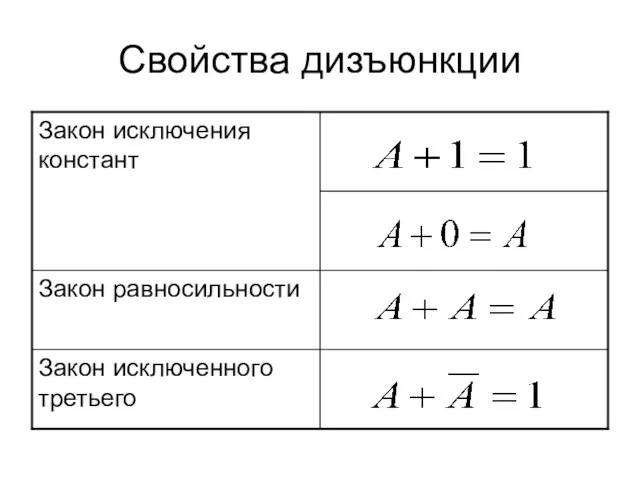
- 9. Свойства дизъюнкции
- 10. Логическое отрицание Инверсия inversio – лат. – переворачиваю Присоединение частицы «не» к сказуемому данного простого высказывания
- 11. Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна. закон
- 12. Логическое следование Импликация implicatio – лат. – тесно связываю Логическое следование соответствует обороту «если…, то…», обозначается
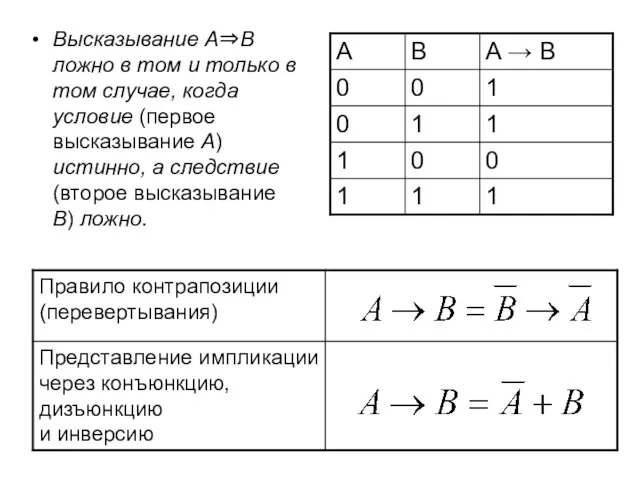
- 13. Высказывание A⇒B ложно в том и только в том случае, когда условие (первое высказывание A) истинно,
- 14. Логическая равносильность Эквиваленция aequivalens – фр. – равноценное или равнозначное соответствует оборотам речи: «тогда и только
- 15. Выражение A⇔B истинно в том и только в том случае, когда оба исходных высказывания одновременно истинны
- 16. Сложение по модулю «2» Соединение двух простых высказываний A и B в одно составное с помощью
- 17. Выражение A⊕B истинно в том и только в том случае, когда значения исходных высказываний не равны
- 18. Закон коммутативности Переместительный закон A+B=B+A A∙B=B∙A
- 19. Сочетательный закон Закон ассоциативности (A+B)+C=A+(B+C) (A ∙ B) ∙ C= A ∙(B ∙ C)
- 20. Распределительный закон Закон дистрибутивности (A+B)∙C=(A∙C)+(B∙C) (A∙B)+C=(A+C)∙(B+C)
- 21. Закон инверсии Формулы де Моргана
- 22. Формулы склеивания (закон исключения)
- 23. Формулы поглощения
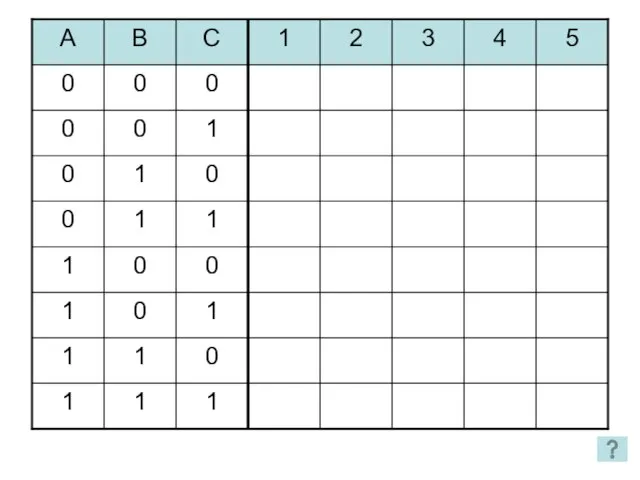
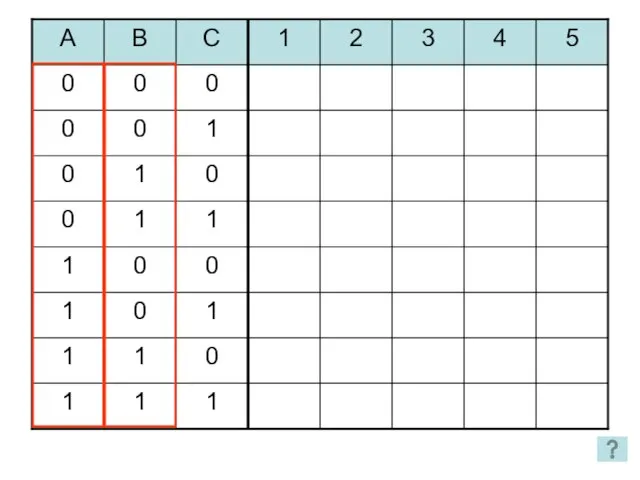
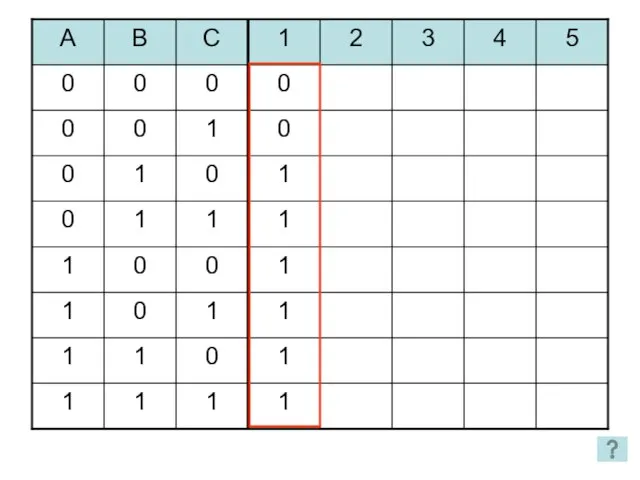
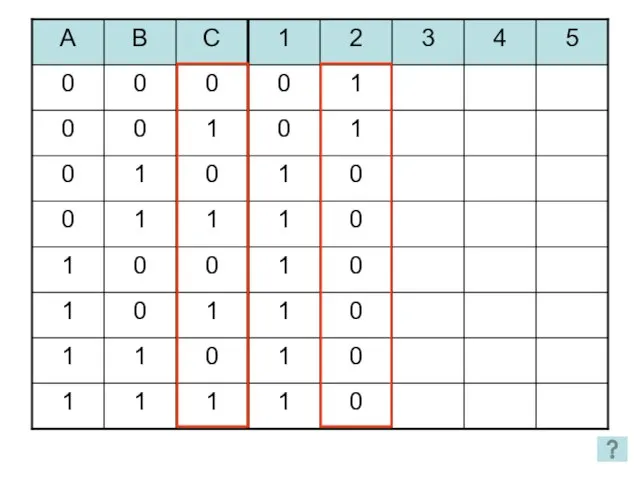
- 25. 1. Является ли данная функция тождественно-истинной? Способы решения: Упрощение функции Построение таблицы истинности
- 26. 1 способ
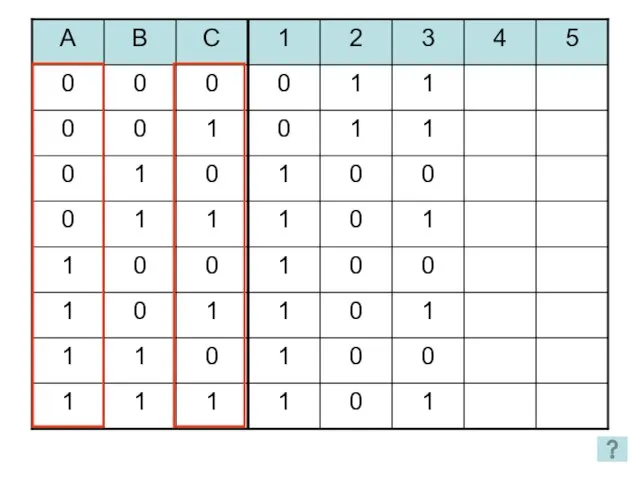
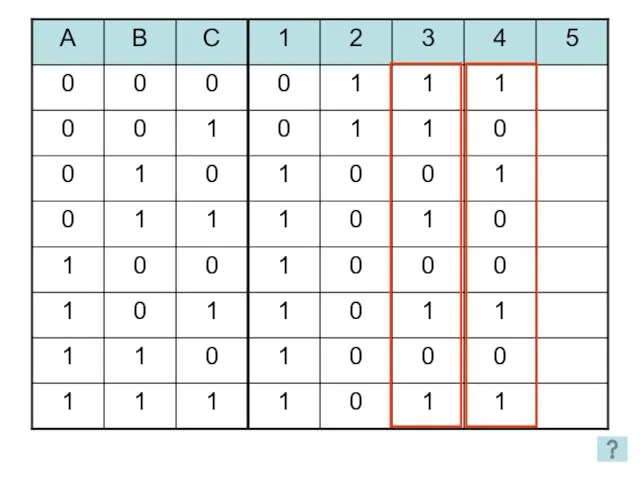
- 27. 1 2 3 4 5 2 способ
- 34. 2. Следующие два высказывания истинны: «неверно, что если магазин А организует распродажу, то магазин С тоже»;
- 35. «Если магазин А организует распродажу, то магазин С тоже» A→C «Неверно, что если магазин А организует
- 36. «Из двух магазинов В и С организует распродажу только один»
- 37. Это возможно только в одном случае, когда A=1, B=1, С=0. То есть, магазины A и B
- 38. 3. На олимпиаде по информатике студенты A, B, C и D заняли первые четыре места. Когда
- 39. D – первый или B – второй: D1+B2=1 C – первый или A – четвертый: C1+A4=1
- 40. 3. Сформулируйте на естественном языке отрицание следующего высказывания: "Виктор пойдет на рыбалку только при солнечной погоде,
- 41. «Виктор пойдет на рыбалку» - A «Будет солнечная погода» - B «Будет жарко» - C Перефразируем
- 42. Будет солнечная погода и нежарко, а Виктор не пойдет на рыбалку.
- 43. Дизъюнктивно-нормальная форма ДНФ — является логической суммой элементарных конъюнкций. Совершенная ДНФ – логическая сумма элементарных конъюнкций,
- 44. Конъюнктивно-нормальная форма КНФ — является логическим произведением элементарных дизъюнкций. Совершенная КНФ – логическое произведение элементарных дизъюнкций,
- 45. Табличный способ приведения к СДНФ Составляем таблицу истинности данной функции. Рассматриваем только те строки таблицы, в
- 46. Табличный способ приведения к СКНФ Составляем таблицу истинности данной функции. Рассматриваем только те строки таблицы, в
- 47. Если условится из двух форм, СДНФ и СКНФ, отдавать предпочтение той, которая содержит меньше букв, то
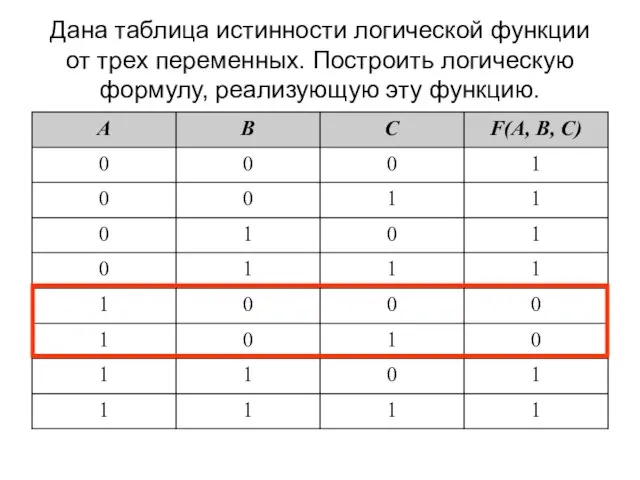
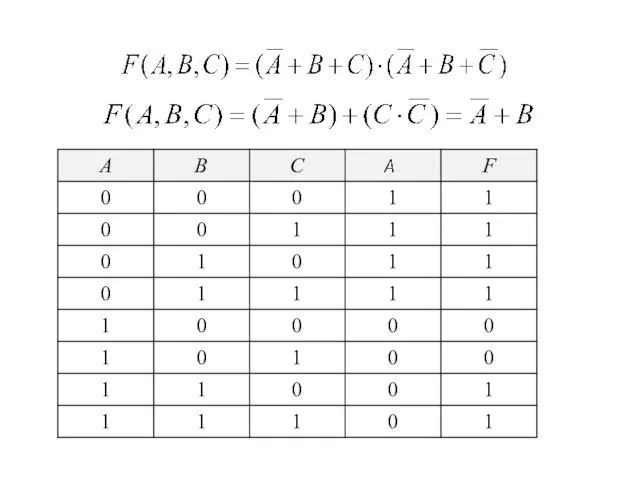
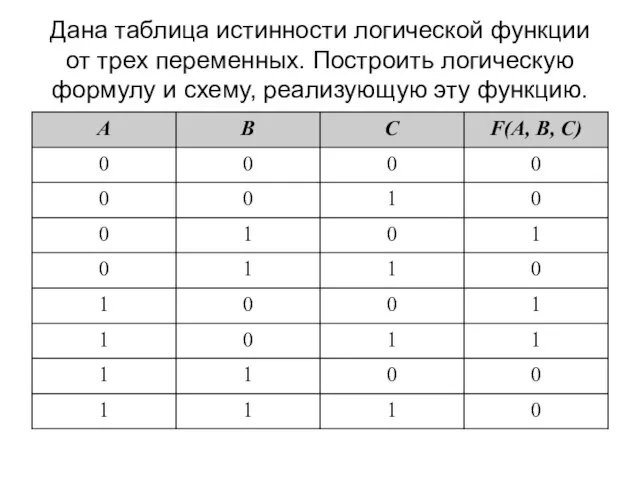
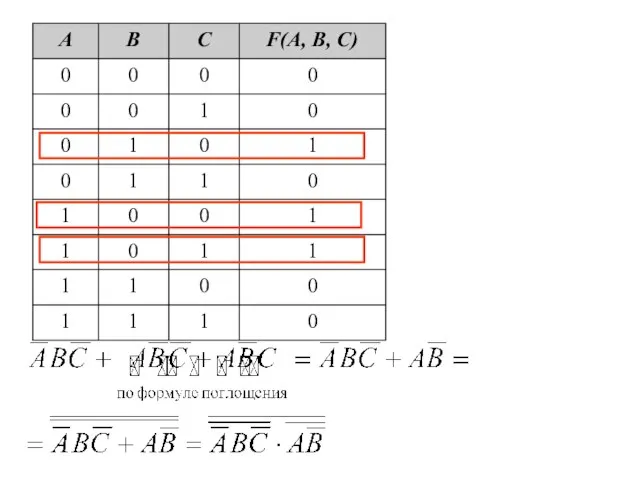
- 48. Дана таблица истинности логической функции от трех переменных. Построить логическую формулу, реализующую эту функцию.
- 50. 4. Построить схему электрической цепи для подъезда трехэтажного здания, чтобы выключателем на любом этаже можно было
- 51. Сначала построим таблицу истинности для требуемой функции. Переменными функции будут выключатели на каждом этаже подъезда. Свет
- 53. Теперь по таблице истинности построим дизъюнктивно-нормальную форму. Отберем те строки в таблице истинности, которые в результате
- 55. Стрелка Пирса (символ Лукашевича) логическая операция с двумя переменными, соответствует обороту речи «ни…, ни…», обозначается следующим
- 56. Стрелка Пирса (символ Лукашевича)
- 57. Штрих Шеффера логическая операция с двумя переменными, соответствует обороту речи «не… или не…», обозначается следующим образом
- 58. Штрих Шеффера
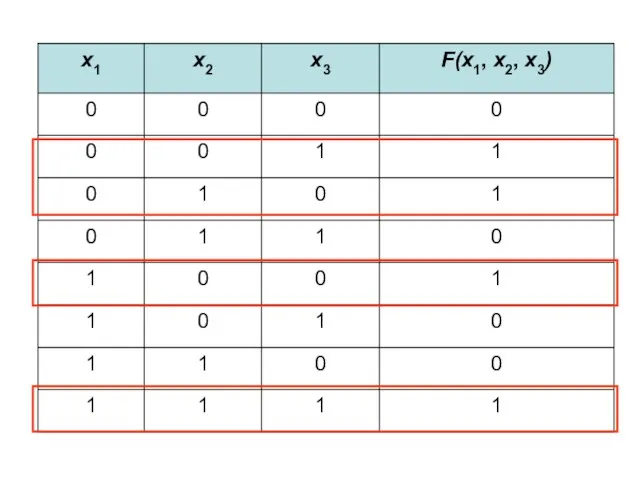
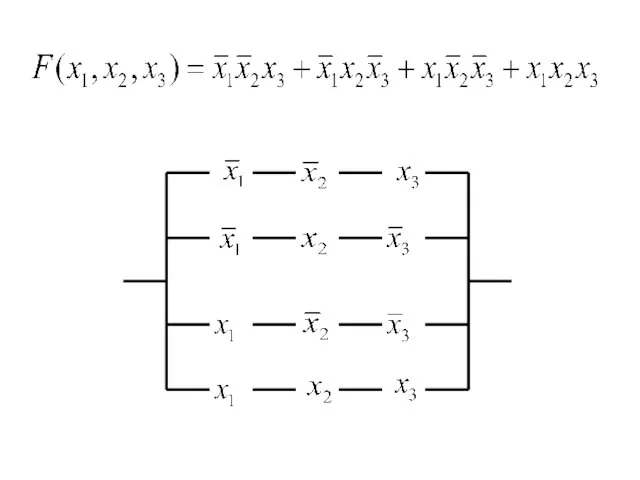
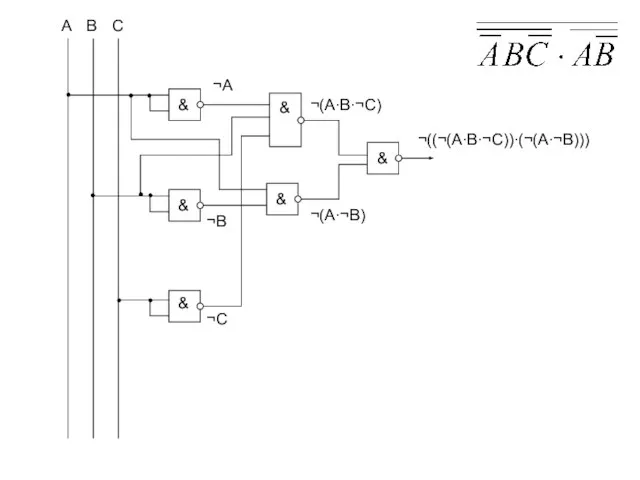
- 59. Дана таблица истинности логической функции от трех переменных. Построить логическую формулу и схему, реализующую эту функцию.
- 61. A B C & & & & & & ¬A ¬B ¬C ¬(A∙B∙¬C) ¬(A∙¬B) ¬((¬(A∙B∙¬C))∙(¬(A∙¬B)))
- 62. 5. После традиционного вечера встречи с выпускниками школы в стенгазете появилась заметка о трех наших бывших
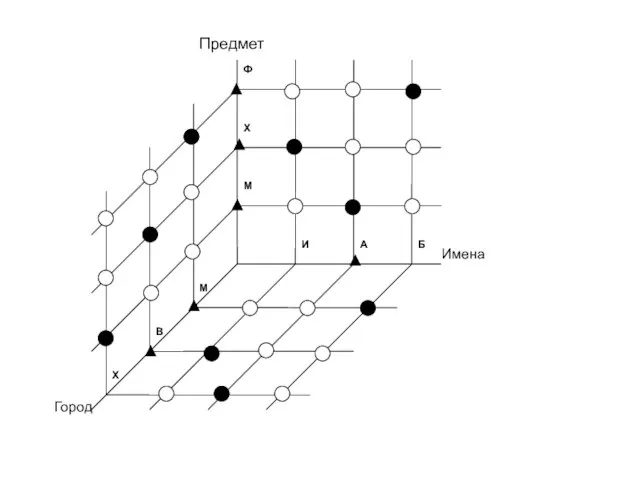
- 63. Алгоритм решения задач на приведение множеств во взаимно-однозначное соответствие Строится пространственная система координат XYZ, на осях
- 64. Правила экстраполяции в плоскости «Темная» экстраполяция. Если на горизонтали (вертикали) все фигуры, кроме одной, светлы, то
- 65. Правило множественного проектирования «Темная» фигура в своей плоскости проектируется на координатные оси. Прямые, проведенные через проекции
- 66. Б А И М Х Ф М В Х Имена Предмет Город
- 68. Скачать презентацию

















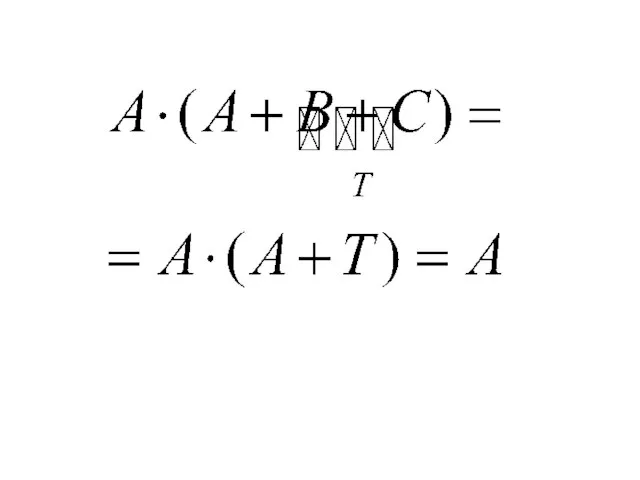

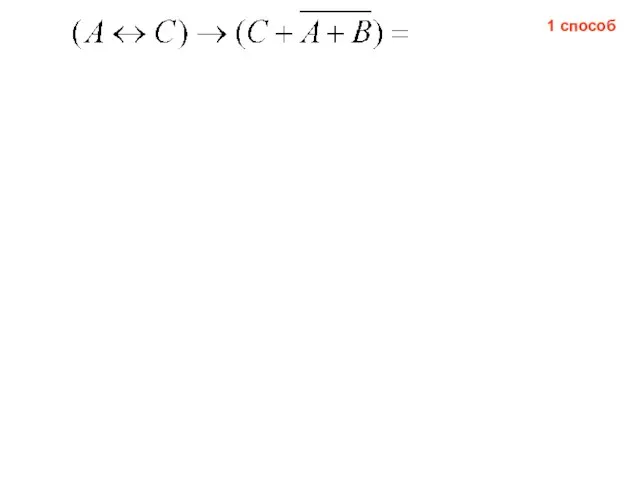
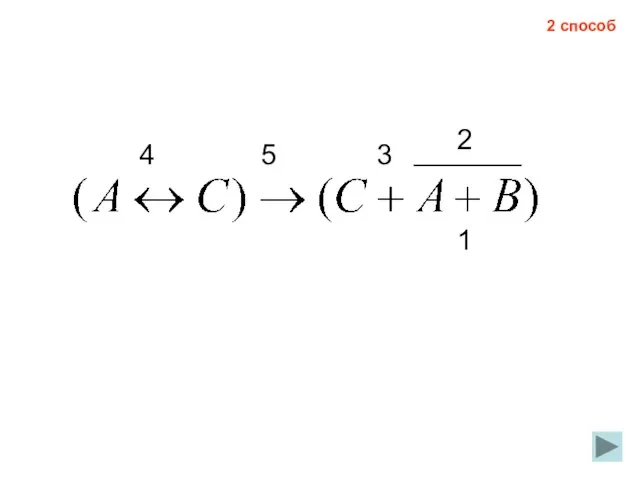

























 Современные возможности пробиотической терапии в клинике внутренних болезней
Современные возможности пробиотической терапии в клинике внутренних болезней Территория смыслов
Территория смыслов Карта пробных ароматов: Al Haramain/Aysha (милая)
Карта пробных ароматов: Al Haramain/Aysha (милая) Понятие мониторинга
Понятие мониторинга Прием письменного вычитания в случаях вида 50-24
Прием письменного вычитания в случаях вида 50-24 Акварельные зарисовки
Акварельные зарисовки Русские народные сказки
Русские народные сказки Красная книга растений
Красная книга растений Биография. Шаблон
Биография. Шаблон Дифференциальная диагностика и принципы лечения синдрома Корнелии Де ЛАНГЕ
Дифференциальная диагностика и принципы лечения синдрома Корнелии Де ЛАНГЕ Презентация на тему Телескоп
Презентация на тему Телескоп Презентация Сушильникова Н.И. Экологическая сказка
Презентация Сушильникова Н.И. Экологическая сказка Телеметрическая платформа M2MGate Solution
Телеметрическая платформа M2MGate Solution Китайский клуб МИИТа
Китайский клуб МИИТа Тема выпускной квалификационной работы. Шаблон
Тема выпускной квалификационной работы. Шаблон Морской порт Санкт-Петербург. Отчет по результатам линейного обхода
Морской порт Санкт-Петербург. Отчет по результатам линейного обхода С днем рождения!!!
С днем рождения!!! Муниципальное дошкольное образовательное учреждение «Детский сад № 15» г. Чебоксары
Муниципальное дошкольное образовательное учреждение «Детский сад № 15» г. Чебоксары Презентация на тему Климат Африки
Презентация на тему Климат Африки Коммуникативный практикум
Коммуникативный практикум Государство. Понятие. Теории происхождения
Государство. Понятие. Теории происхождения Жизнь прекрасна
Жизнь прекрасна Измерение расхода. FR — лидер в новейшей высокоточной технологии измерения расхода
Измерение расхода. FR — лидер в новейшей высокоточной технологии измерения расхода Венев
Венев ПУТЕШЕСТВИЕ ПО МАТЕРИКАМ
ПУТЕШЕСТВИЕ ПО МАТЕРИКАМ Экономия водоснабжения
Экономия водоснабжения Рифмоплёт
Рифмоплёт Вареники с картошкой
Вареники с картошкой