Содержание
- 2. Prime Numbers An integer p is a prime number if it has no factors other than
- 3. Factorisation Given an integer n, there is an efficient algorithm to determine whether n is composite
- 4. The fastest factorisation algorithm at the moment is called the “Number Field Sieve” but even this
- 5. Important to Note: Determining whether a large number is prime or composite is easy; Multiplying 2
- 6. Fermat’s Little Theorem If p is a prime number and a is any number between 1
- 7. Solving a problem Suppose I have a prime number p; a number m between 1 and
- 8. Yes you can if you take the following steps: Find a number d such that e*d=1
- 9. Why does that work? We found d such that e*d = 1 mod p-1 That means
- 10. 2. We computed cd mod p But cd = (me)d mod p = med mod p
- 11. This works because of Fermat’s Little Theorem. We know that since p is a prime we
- 12. Why doesn’t it work? In general an-1 ≠ 1 mod n if n is not prime.
- 13. Finding r In order to find r such that ar = 1 mod n, you have
- 14. Important to note now: It is easy to determine whether a large number is prime or
- 15. Given e (co-prime with r), it is easy to determine d such that (e*d) =1 mod
- 16. This is the basis of the RSA public key cryptosystem. The holder of the public key
- 17. RSA – Key Generation Bob generates two large primes p and q (each with approx. 100
- 18. He computes the private key d by solving the equation (e*d) =1 mod r. He can
- 19. RSA - Encryption Alice wishes to send Bob a message m. She takes the following steps:
- 20. RSA - Decryption Bob receives the value c from Alice. He decrypts it using his private
- 22. Скачать презентацию








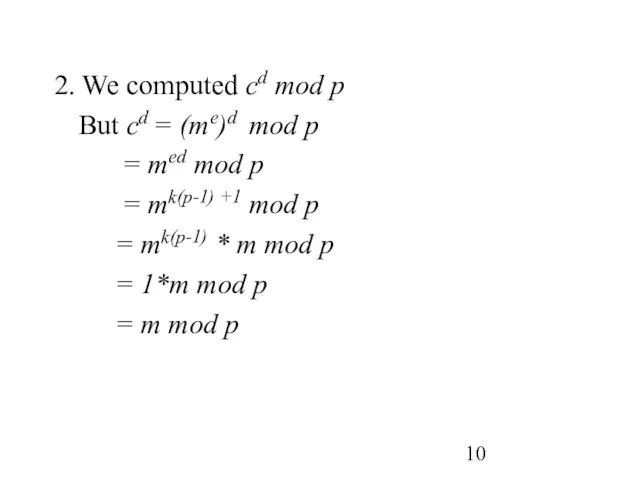










 ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА «Сорные растения моего огорода»
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА «Сорные растения моего огорода» Работа сортировочной станций
Работа сортировочной станций Применение галогенов и их соединений
Применение галогенов и их соединений Опале листя: користь чи
Опале листя: користь чи ДЖОЗЕФ ДЖОН ТОМСОН (1856-1940) ПРЕДЛОЖИЛ ПЕРВУЮ МОДЕЛЬ АТОМА - «ПУДИНГ С ИЗЮМОМ»
ДЖОЗЕФ ДЖОН ТОМСОН (1856-1940) ПРЕДЛОЖИЛ ПЕРВУЮ МОДЕЛЬ АТОМА - «ПУДИНГ С ИЗЮМОМ» Орден Александра Невского в истории моей семьи
Орден Александра Невского в истории моей семьи Презентация на тему Приготовление блюд из фруктов (5 класс)
Презентация на тему Приготовление блюд из фруктов (5 класс) Жемчужина России - Северный Кавказ. Заочное путешествие
Жемчужина России - Северный Кавказ. Заочное путешествие CHEMISTRY IN OUR LIFE
CHEMISTRY IN OUR LIFE  Битва за Москву. (30.09.1941 - 20.04.1942)
Битва за Москву. (30.09.1941 - 20.04.1942) Украшение. Для мальчиков. Для девочек
Украшение. Для мальчиков. Для девочек Презентация на тему Натюрморт в графике
Презентация на тему Натюрморт в графике ЭФФЕКТИВНЫЕ ЦЕМЕНТНЫЕ КОМПОЗИТЫ, МОДИФИЦИРОВАННЫЕ ВОДОРАСТВОРИМЫМИ АДДУКТАМИ НАНОКЛАСТЕРОВ УГЛЕРОДА Низина Татьяна Анатольев
ЭФФЕКТИВНЫЕ ЦЕМЕНТНЫЕ КОМПОЗИТЫ, МОДИФИЦИРОВАННЫЕ ВОДОРАСТВОРИМЫМИ АДДУКТАМИ НАНОКЛАСТЕРОВ УГЛЕРОДА Низина Татьяна Анатольев Решение нестандартных задач по математике 6 класс
Решение нестандартных задач по математике 6 класс Шкала типов личности
Шкала типов личности Внеурочная деятельность
Внеурочная деятельность Ячменев Александр Александрович
Ячменев Александр Александрович Города Науки
Города Науки Презентация на тему Самопрезентация учителя начальных классов
Презентация на тему Самопрезентация учителя начальных классов Проблемы психологической герменевтики
Проблемы психологической герменевтики Особенности правового регулирования деятельности в сети ИнтернетАлексей Пономарев юрист2011
Особенности правового регулирования деятельности в сети ИнтернетАлексей Пономарев юрист2011 Защита детей от жестокого обращения
Защита детей от жестокого обращения Управленческая модель «Центры подготовки кадров - эффективная модель частно-государственного и общественного управления професс
Управленческая модель «Центры подготовки кадров - эффективная модель частно-государственного и общественного управления професс Масленица
Масленица Исследование верхнего и нижнего течения реки Охта в Санкт-Петербурге.Начало исторического исследования.
Исследование верхнего и нижнего течения реки Охта в Санкт-Петербурге.Начало исторического исследования. Презентация на тему О плане и планировании воспитательной работы в классе
Презентация на тему О плане и планировании воспитательной работы в классе  Задержка психического развития методы коррекции
Задержка психического развития методы коррекции Выполнила:учитель обществоведениявысшей квалификационной категорииСорокина О.В.
Выполнила:учитель обществоведениявысшей квалификационной категорииСорокина О.В.