Шалаев Ю.Н. каф. Информатики и проектирования систем. Институт кибернетикиТеория случайных функций

Если параметр t – время, то случайную функцию называют случайным процессом. Для дискретного случая – случайной последовательностью.
Если зафиксировать элементарное событие ω=ω0, то X(t, ω0) будет неслучайной функцией аргумента t.
Конкретный вид случайной функции при фиксированном ω в данном опыте называется реализацией случайной функции X(ωI,t). Если зафиксировать параметр случайной функции при
t=tk, то она будет зависеть только от элементарного события и, следовательно, станет случайной величиной X(tк, ω). При дальнейшем изложении аргумент ω для краткости опускается.

Законы распределения случайных функций
Случайную функцию рассматривают как многомерную случайную величину. То есть X(t)
можно представить как систему случайных величин:
{X(t1), X(t2), …, X(tn)}, t1

F2(x1, x2; t1,t2)=P{X(t1)
Fn(x1, x2,…xn; t1,t2…tn)=P{X(t1) t2…tn – произвольная последовательность значений аргумента t, взятая из области его значений.
x1, x2,…xn – последовательность неслучайных вещественных переменных величин.

Для непрерывных случайных функций X(t) плотности распределения находятся как
f1(x1; t1)=∂ F1(x1; t1)/∂x1, f2(x1, x2; t1, t2)=∂∂ F2(x1, x2;t1,t2)/∂x1∂x2,
fn(x1, x2,…xn; t1, t2…tn)=∂ n Fn(x1, x2,…xn; t1, t2…tn)/∂x1…∂xn
Их называют плотностями распределения первого, второго и n –го порядка.

Для плотностей распределения случайной функции X(t) имеет место интегральные соотношения:
Для независимых сечений X(t) n-мерная плотность вероятностей выразится через одномерную плотность распределения вероятностей формулой

Характеристики случайных функций
Математическое ожидание случайной функции
Математическим ожиданием случайной функции X(t) называется неслучайная функция mx(t), которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции:
Математическое ожидание случайной функции X(t) представляет собой некоторую среднюю функцию, около которой группируются и относительно которой колеблются все возможные реализации случайной функции.

Свойства математического ожидания
Математическое ожидание неслучайной (детерминированной) функции равно самой этой функции
MC(t)=C(t).
Неслучайную функцию можно выносить за оператор математического ожидания
MC(t)X(t)=C(t)MX(t).
M(X(t)±Y(t))=MX(t)±MY(t).
Для некоррелированных X(t) и Y(t)
MX(t)Y(t)=MX(t)MY(t).

Дисперсия случайной функции
Дисперсией случайной функции X(t) называется неслучайная функция Dx(t), значение которой для каждого t равно дисперсии соответствующего сечения случайной функции
Дисперсия характеризует разброс возможных реализаций случайной функции относительно среднего. Обладает свойствами дисперсии случайной величины.

Корреляционная функция случайной функции X(t)
Корреляционной функцией случайной функции X(t) называется неслучайная функция двух аргументов t1 и t2, которая при каждой паре значений t1 и t2 равна корреляционному моменту соответствующих сечений случайной функции:
После преобразования Kx(t1,t2), получим
Kx(t1,t2)=M(X(t1)X(t2))-mx(t1)mx(t2).

Корреляционная функция находится как
Для независимых сечений случайной функции корреляционная функция равна нулю.

Свойства корреляционной функции
Дисперсия случайной функции находится при равенстве аргументов t1=t2=t:
DX(t)=Kx(t,t).
Корреляционная функция вещественной случайной функции симметричная функция:
Kx(t1,t2)= Kx(t2,t1).
Kx(t1,t2) убывает по мере увеличения длины интервала (t1,t2).
Для вещественной случайной функции

Линейные преобразования случайных функций
Прибавление неслучайного слагаемого
Пусть X(t) – случайная функция, а C(t) – неслучайная функция:
Y(t)=X(t)+C(t).
Математическое ожидание:
MY(t)=mx(t)+C(t).
Корреляционная функция:
Ky (t1,t2)= Kx(t1,t2).

Умножение на неслучайный множитель
Рассмотрим случайную функцию
Y(t)=X(t)*C(t).
Математическое ожидание:
MY(t)=MX(t)*MC(t)=C(t)*MX(t).
Корреляционная функция:
Ky(t1,t2)=C(t1)C(t2)Kx(t1,t2).

Дифференцирование случайной функции
Пусть X(t) – случайная функция и заданы математическое ожидание mx(t) и корреляционная функция Kx(t1,t2). Найдем характеристики случайной функции Y(t)=dX(t)/dt.
Математическое ожидание:
MY(t)=dmx(t)/dt.
Функция корреляции:
Ky(t1,t2)=∂∂Kx(t1,t2)/∂t1∂t2.

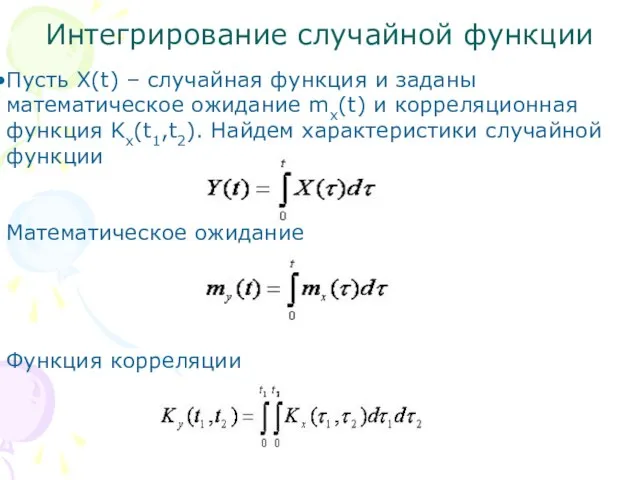
Интегрирование случайной функции
Пусть X(t) – случайная функция и заданы математическое ожидание mx(t) и корреляционная функция Kx(t1,t2). Найдем характеристики случайной функции
Математическое ожидание
Функция корреляции

Сложение случайных функций
Рассмотрим сумму случайных функций:
Z(t)=X(t)+Y(t).
Найдем характеристики Z(t):
По теореме сложения математических ожиданий получим:
mz(t)=M((X(t)+Y(t))=mx(t)+my(t)).
Из определения корреляционной функции:
После преобразования, получим:

Взаимная корреляционная функция:
Корреляционная функция связи характеризует степень зависимости значения случайной функции X(t) взятого в момент t1, от значения случайной функции Y(t) взятого в момент t2.
Kx(t1,t2) – корреляционная функция связи одной случайной величины, поэтому иногда ее называют «автокорреляционной функцией».

Свойства взаимной корреляционной функции
Для действительных случайных функций перестановка индексов при одновременной перестановке аргументов не меняет значения
взаимной корреляционной функции:
Rxy(t1,t2)=Ryx(t2,t1).
Взаимная корреляционная функция не изменяется при прибавлении любых неслучайных слагаемых.
Если взаимная корреляционная функция равна нулю:
Rxy(t1,t2)=0,
то функции X(t) и Y(t)) называются некоррелированными (несвязанными).

Сложение случайной функции со случайной величиной
Пусть X(t)-случайная функция, ξ-случайная величина; они некоррелированы. Получим случайную функцию Z(t)=X(t)+ ξ и определим ее характеристики при известных mx(t) и Kx(t1,t2):
MZ(t)=mz(t)=mx(t)+M ξ.
Для корреляционной функции получим:
Kz(t1,t2)=Kx(t1,t2)+Kξξ= Kx(t1,t2)+Dξ.

Нормированная взаимная корреляционная функция связи
Это безразмерная характеристика связи между случайными функциями:

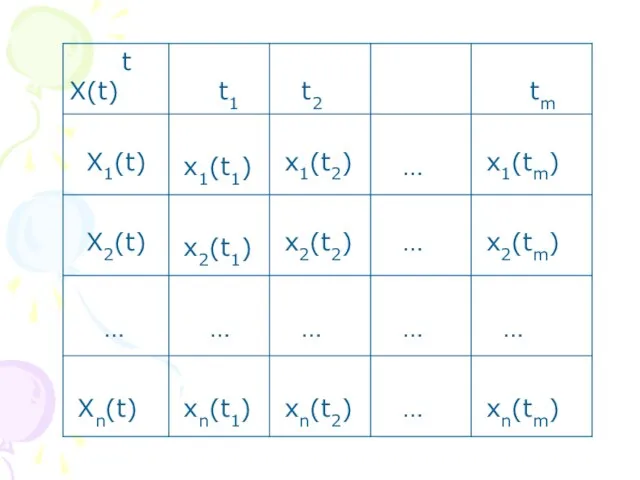
Оценка характеристик случайной функции
Пусть имеется n реализаций случайной функции X(t): x1(t),x2(t),…, xn(t). Требуется найти оценки характеристик случайной функции: mx(t), Dx(t) и Kx(t1,t2). Для этого рассмотрим ряд сечений X(t) для моментов t1,t2,…, tm. Каждому из этих моментов будет соответствовать n значений случайной функции. Моменты задаются обычно равноотстоящими или из технических условий.
Значения X(t) заносятся в таблицу:

Каждое сечение tk есть n значений случайной величины и оценка математического ожидания находится по известному соотношению:
Получим m точек оценки функции математического ожидания. Это усреднение по множеству реализаций. ∧
Оценка не смещена, так как Mm(t)=m(t).
Для дисперсии:

Для корреляционной функции:
По полученным значениям можно построить функцию математического ожидания и дисперсии по точкам, а функция корреляции двух аргументов воспроизводится по ее значениям в прямоугольной сетке.
Эти функции можно аппроксимировать аналитическими выражениями.

Стационарные случайные функции
Различают стационарность случайной функции в узком и в широком смысле. Стационарность в узком смысле случайной функции называется такая случайная функция X(t), для которой n-мерная плотность распределения вероятностей
fn(x1, x2,…xn; t1, t2…tn) при любом n зависит только от величины интервалов t2-t1, t3-t1,…,
tn-t1 и не зависит от положения этих интервалов в области изменения аргумента t.

Так, одномерная плотность распределения вероятностей f1(x;t) стационарной в узком смысле не будет зависеть от t – f(x). Двумерная будет зависеть от разности t2-t1=τ то есть f2(x1,x2;τ). N-мерная будет зависеть только от их разностей τ1= t2-t1, τ2= t3-t1,…, τn-1= tn-t1, то есть
fn(x1, x2,…xn; τ1, τ2…τn-1).

Стационарная функция называется стационарной в широком смысле, если ее математическое ожидание постоянно, а корреляционная функция зависит только от разности аргументов τ=t2-t1:
mx(t)=const; Kx(t1,t2)=Kx(τ).

Стационарная функция в широком смысле может быть нестационарной в узком смысле. Наоборот, случайная функция стационарная в узком смысле, является стационарной в широком смысле:

Свойства Kx(τ)
Если X(t) вещественная и стационарная, то ее корреляционная функция является четной функцией:
Kx(τ)= Kx(-τ).
Если X(t) стохастически непрерывна, то ее корреляционная функция Kx(τ) есть функция непрерывная.
Если X(t) вещественная и стационарная, то имеет место неравенство
|Kx(τ)|≤Kx(0).

Эргодические свойства стационарных случайных функций
Так как X(t) вещественная и стационарная и процесс протекает однородно по времени, то по одной реализации достаточной продолжительности можно оценить характеристики случайной функции.
Эргодическое свойство состоит в том, что каждая отдельная реализация Xk(t) несет как бы информацию всей совокупности возможных реализаций X(t), т.е. одна реализация достаточной продолжительности может заменить при обработке множество реализаций.

Оценка характеристик стационарной случайной функции
Если X(t) обладает эргодическим свойством, то для нее среднее по времени приближенно равно среднему по множеству наблюдений.
Для mx(t)=const:

Для корреляционной функции:
где
Тогда
Вычислив интеграл для ряда τ, можно приближенно воспроизвести по точкам весь ход корреляционной функции.

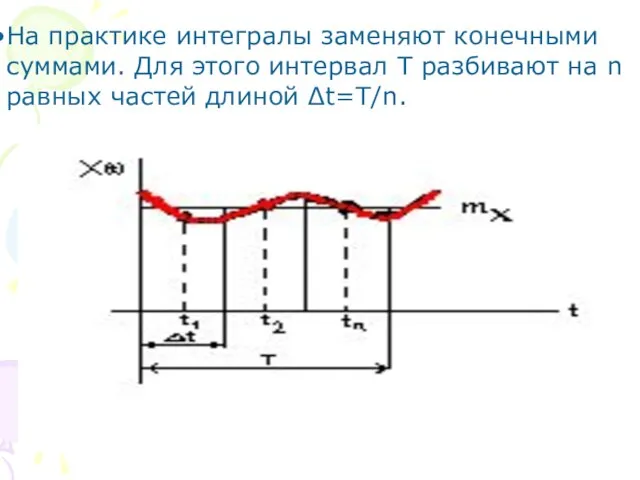
На практике интегралы заменяют конечными суммами. Для этого интервал Т разбивают на n равных частей длиной Δt=T/n.

Обозначим середины полученных участков
t1, t2,…, tn, тогда получим:
Для корреляционной функции введем: τ=mΔt=mT/n.
Для интервала интегрирования:
T-τ=T-mT/n=(n-m)/n·T, 1/(T-τ)=n/(n-m)·T.
Тогда получим оценку корреляционной функции:

m=0, 1, 2,….
Вычисления проводятся до тех m при которых корреляционная функция становится равной нулю.

Марковский случайный процесс
Случайный процесс называется Марковским, если все вероятностные характеристики процесса в будущем зависят лишь от того, каким образом этот процесс протекал в прошлом.
То есть будущее зависит от прошлого только через настоящее.

Пусть A={a1, a2,…, an} – пространство исходов эксперимента или пространство состояний некоторой системы, одинаковые для каждого шага случайного процесса. Тогда по определению Марковского процесса вероятность того, что система переходит из состояния ai в состояние ak зависит только от состояния ai из которого она исходит в процессе рассматриваемого перехода и не зависит от того, каким образом система пришла в это состояние.

Случайный процесс, протекающий в физической системе называется цепью Маркова, если переходы системы из одного состояния в другое возможны только в определенные дискретные моменты времени t1, t2,…. Обозначим через Pik вероятности перехода системы из состояния ai в состояние aк. Марковская цепь характеризуется тем, что вероятности Pik определяются для всех упорядоченных пар состояний и задано исходное состояние.

Вероятности перехода Р11, Р22, Р33 означают, что система остается в состоянии а1 с вероятностью Р11, в состоянии а2 → Р22, а3 → Р33. Равенство нулю вероятности Pik означает невозможность соответствующих переходов.
Вероятности перехода из одного состояния в другое можно представить двумя способами.

Первый способ состоит в том, что вероятности перехода записываются в виде квадратной матрицы.
Для Марковской цепи с тремя состояниями
а1, а2, а3 матрица имеет вид:
Матрица вероятностей перехода (стохастическая матрица) должна обладать условием, что сумма элементов каждой строки равна единице.

Второй способ представления вероятностей перехода состоит в построении диаграммы перехода, когда возможные состояния системы S наглядно изображают с помощью графа состояний. Возможные состояния системы на графе изображаются окружностями. Вероятности перехода изображаются ребрами с соответствующими числами вероятностей перехода. Сумма вероятностей для ребер, выходящих из любой вершины графа должна равняться единице. По матрице можно построить граф и наоборот.

При изучении Марковских цепей иногда возникает задача: найти вероятности того, что через n шагов процесс перейдет из состояния ai в состояние ak. Зная матрицу Pn можно найти матрицу Pn+1 по соотношению:
Pn+1=P·Pn.

Марковская цепь называется регулярной, если какая – либо степень ее матрицы вероятностей перехода не содержит нулевых элементов. Любая стохастическая матрица, не содержащая нулей, определяет регулярную Марковскую цепь.

Марковская цепь называется эргодической, если из каждого ее состояния можем попасть в любое другое состояние.

Моделирование случайных величин
Случайные величины моделируют
с помощью преобразований одного
Или нескольких независимых
Значений случайной величины L,
равномерно распределенной в
интервале (0,1).

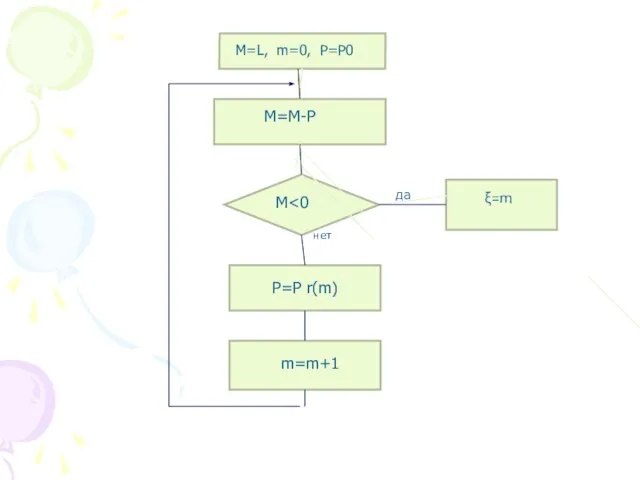
Моделирование дискретных случайных величин
Общий метод моделирования основан на следующем очевидном равенстве
которые связаны рекурсивными формулами
и моделирование производится по схеме

да
нет
M=L, m=0, P=P0
M=M-P
M<0
P=P r(m)
m=m+1
ξ=m

Для биномиального распределения с параметрами (P,n)

Для распределения Пуассона с параметром a

Моделирование непрерывных случайных величин
Случайная величина моделируется по
формуле вида:
ξ=φ(L),
где φ(L) – строго монотонная и непрерывная функция на
интервале (0,1). Для случайной величины ξ задана плотность
распределения f(x) на интервале (а, в). Для монотонно
возрастающей функции φ(L) моделирующая формула для
непрерывной случайной ξ запишется в виде

Для монотонно убывающей функции φ(L)
моделирующая формула для непрерывной
случайной ξ запишется как
которая эквивалентна предыдущей формуле
т. к. случайные величины 1-L и L одинаково
распределены.