Системы счисления Системы счисления делятся на позиционные и непозиционные. В позиционной системе вес цифры зависит от ее позиции

Позиционные системы счисления
Количество цифр в СС называется ее основанием.
Позиция цифры в числе называется ее разрядом, а количество цифр в числе его разрядностью.
Десятичная система счисления.
Цифры 0,1,2,3,…9
Основание = 10
Например: 1221 – 4-х разрядное число.
Вес единиц – 1000 и 1, вес двоек 200 и 20
Разложим это число по степеням основания:
3 2 1 0 – номера разрядов (разряды нумеруются справа налево от 0) 1 2 2 1=1∙103+2∙102+2∙101+1∙100 =1000+200+20+1
Каждую цифру умножаем на основание (10)в степени равной разряду

Двоичная система счисления
Цифры 0,1
Основание = 2
Например: 111112 – 5-и разрядное двоичное число.
Вес единиц – 1,2,4,8,16 справа налево
Для примера, разложим число 100012 по степеням основания для перевода двоичного числа в десятичную систему счисления:
4 3 2 1 0 – номера разрядов 1 0 0 0 12 =1∙24+0∙23+0∙22+0∙21+1∙20=16+0+0+0+1=17
Каждую цифру умножаем на основание (число 2)в степени = разряду, складываем произведения и получаем десятичный эквивалент двоичного числа 100012=17

Правило обратного перевода (из десятичной СС в двоичную):
Целочисленное деление десятичного числа на 2 несколько раз, пока в частном не получится 1. Записать 1 и приписать к ней все остатки целочисленного деления в обратном порядке.
Ответ: 13=11012
Проверка разложением по степеням основания:
3 2 1 0 – номера разрядов
1 1 0 12 =1∙23+1∙22+0∙21+1∙20=23+22+20=8+4+1=13

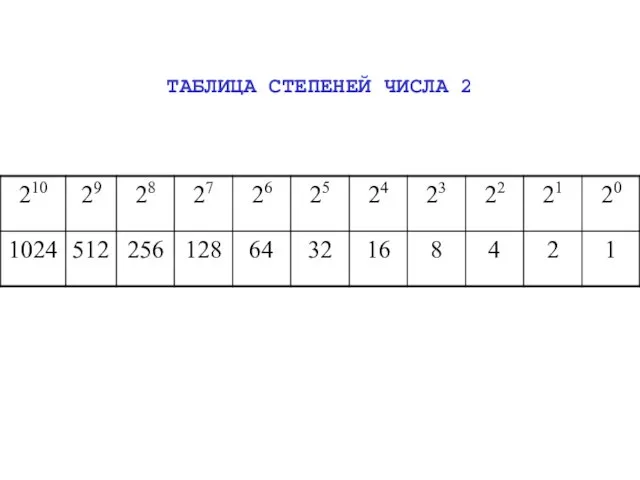
ТАБЛИЦА СТЕПЕНЕЙ ЧИСЛА 2

Перевод из десятичной системы счисления в двоичную вычитанием степеней двойки
Задание: перевести свой день рождения в двоичную систему счисления двумя способами
Сложение в двоичной системе счисления
12 12 110112=27
02 12 100112=19
12 102 1011102=46

Восьмеричная система счисления.
Цифры: 0,1,2,…,7
Основание = 8
Для перевода числа из 8-ричной СС в 10-ную разложим его по степеням основания (восьмерки).
Например: 1278
2 1 0
1 2 78 =1·82+2·81+7·80=64+16+7=87
Обратный перевод: 197 = 3058
Правило обратного перевода:
Целочисленное деление на 8 несколько раз пока в частном не получим цифру<8, затем записываем эту цифру и приписываем все остатки целочисленного деления в обратном порядке.
Задание: перевести свой год рождения в 8-ричную систему счисления.

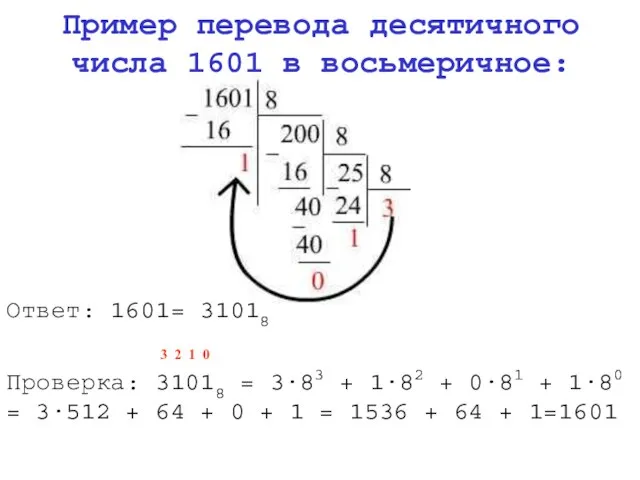
Пример перевода десятичного числа 1601 в восьмеричное:
Ответ: 1601= 31018
3 2 1 0 Проверка: 31018 = 3∙83 + 1∙82 + 0∙81 + 1∙80 = 3∙512 + 64 + 0 + 1 = 1536 + 64 + 1=1601

Шестнадцатеричная система счисления.
Цифры: 0,1,2,…,9,A,B,C,D,E,F
Основание = 16
Для перевода числа из 16-ричной СС в 10-ную разложим его по степеням основания (16-ти).
Например: А0516
2 1 0
А 0 516 =10·162+0·161+5·160=2560+0+5=2565
Обратный перевод: 2565 = А0516
Правило обратного перевода:
Целочисленное деление на 16 несколько раз пока в частном не получим цифру<16, затем записываем эту цифру и приписываем все остатки целочисленного деления в обратном порядке.
Задание: перевести свой год рождения в 16-ричную систему счисления.

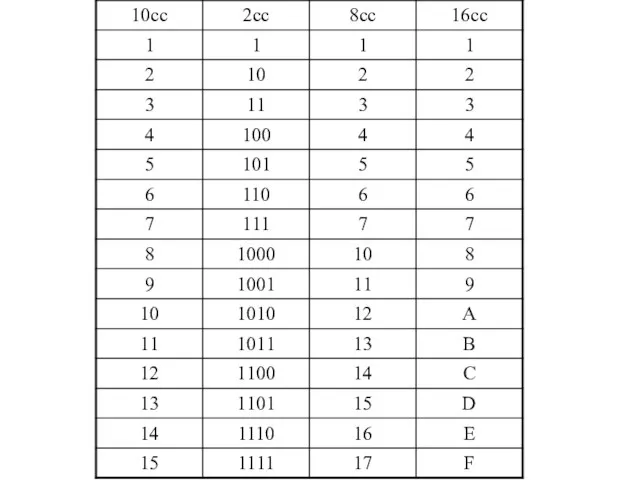
Таблица перевода первых 15 чисел натурального ряда из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную.

8-ми и 16-ричная СС используются как промежуточные между десятичной и двоичной СС. Перевести число из двоичной в 8-ми или 16-ричную системы очень легко. Так же легко сделать обратный перевод.
Перевод из двоичной системы счисления в восьмеричную и шестнадцатеричную (2 8) (2 16)
Триада – три двоичных разряда
2 8 Разбиваем двоичное число на триады справа налево и каждую триаду записываем восьмеричным числом 1.011.101.1102=13568
8 2 Каждую цифру восьмеричного числа записываем как триаду 15338 = 1.101.011.0112
Тетрада – четыре двоичных разряда
2 16 Разбиваем двоичное число на тетрады справа налево и каждую тетраду записываем 16-ричным числом 1.0111.1011.10102=17BA16
16 2 Каждую цифру 16-ричного числа записываем как триаду 1F0316 = 1.1111.0000.00112

Три способа перевода чисел из одной системы счисления в другую