Слайд 2НОРМАЛЬНЫЙ ЗАКОН
Def
μ - параметр сдвига, - параметр масштаба
~N(0;1) – стандартный
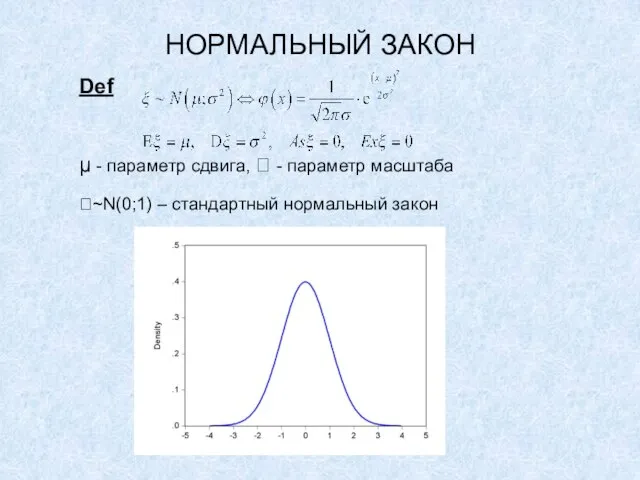
нормальный закон
Слайд 3ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ
Свойства нормального распределения:
~N(μ;2), a, b => a+b~N(aμ+b;a22)
устойчивость относительно линейного преобразования.
Так же

этим свойством обладают распределения:
~U[m1;m2] => a+b~U[am1+b;am2+b] - равномерное
~Exp(λ,) => a+b~ Exp(aλ; a+b) - экспоненциальное
~L(λ,) => a+b~L(aλ; a+b) - Лапласа
~Λ(μ;) => a+b~Λ(aμ+b;a) - логистическое
~C(μ;) => a+b~C(aμ+b;a) - Коши
Найдите формулы плотностей и докажите, что свойство линейности выполняется, в т.ч. и для N(μ;2)
Слайд 4ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ
Свойства нормального распределения:
Пример
~Exp(λ,) => a+b~ Exp(aλ; a+b) - экспоненциальное
λ - характеризует

время ожидания некоторого события
- характеризует момент времени, с которого мы ожидаем проявление события
aλ - изменение масштаба времени
a+b – сдвиг момента времени (в новом масштабе), с которого будем ожидать появление события
Слайд 5ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ
Свойства нормального распределения:
устойчивость относительно линейного преобразования
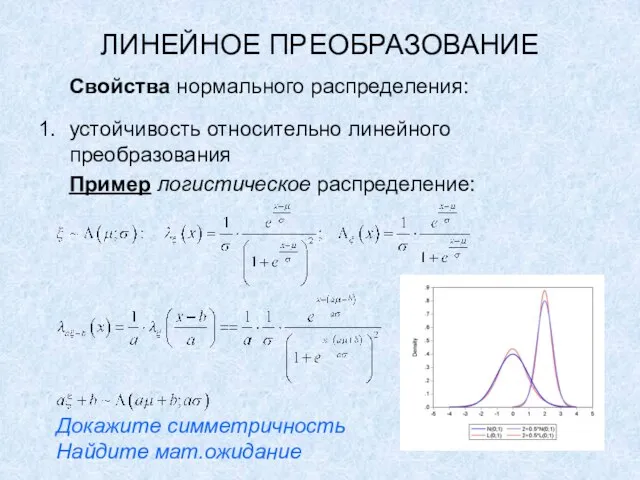
Пример логистическое распределение:
Докажите симметричность
Найдите мат.ожидание
Слайд 6ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ
Свойства нормального распределения:
устойчивость относительно умножения на константу.
~ P(k;θ) => a~ P(ak;θ)

- Парето
~ W(k;λ) => a~ W(k;aλ) - Вейбула
~Г(k;θ) => a~Г(k;aθ) – гамма-распределение
Найдите формулы плотностей и докажите, что это свойство выполняется
Слайд 7ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ
Свойства нормального распределения:
Пример
~ P(k;θ) => a~ P(ak;θ) - распределение доходов
k –
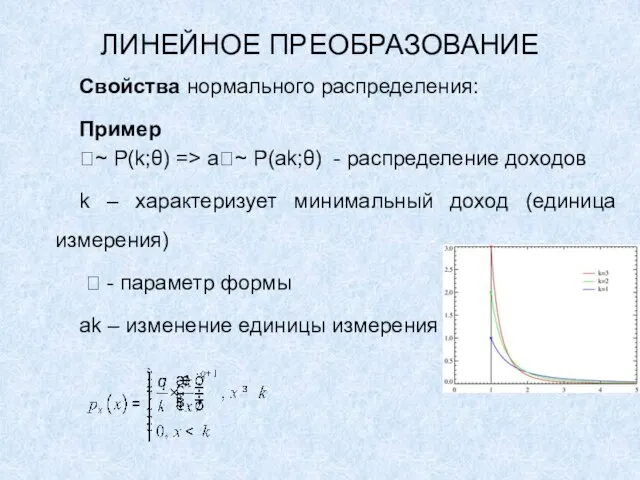
характеризует минимальный доход (единица измерения)
- параметр формы
ak – изменение единицы измерения
Слайд 8УСТОЙЧИВОСТЬ ПО СЛОЖЕНИЮ
Свойства нормального распределения:
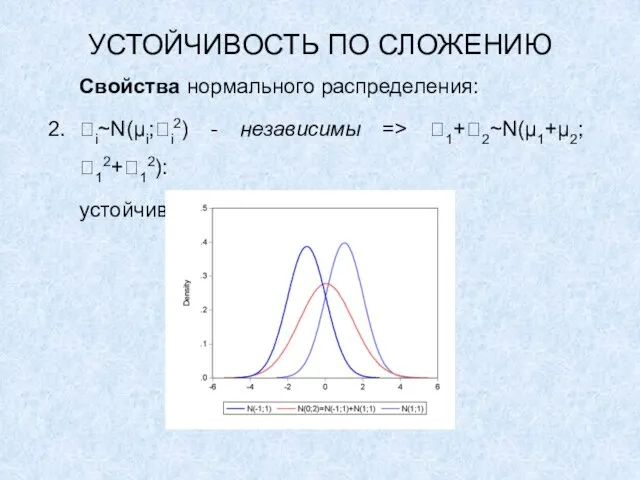
i~N(μi;i2) - независимы => 1+2~N(μ1+μ2;12+12):
устойчивость по сложению.
Слайд 9УСТОЙЧИВОСТЬ ПО СЛОЖЕНИЮ
Свойства нормального распределения:
Устойчивостью по сложению независимых с.в. обладают также:

i~B(ni;p) => Σi~B(Σni;p) - биномиальное
i~Poiss(λi) => Σi~Pois(Σλi) - пуассоновское
i~Г(ki;θ) => Σi~Г(Σki;θ) – гамма распределение
i~2(ki) => Σi~2(Σki) – Хи-квадрат
Докажите это свойство для пуассоновского распределения
i~Exp(λ;0) => Σi~Г(k;λ) – экспоненциальное сворачивается в гамма-распределение при суммировании
Слайд 10УСТОЙЧИВОСТЬ ПО СЛОЖЕНИЮ
Свойства нормального распределения:
Примеры
i~B(ni;p) => Σi~B(Σni;p) - биномиальное
p – вероятность успеха
n

– длина сери испытаний
EΣi=pΣni – ожидаемое число успехов не зависит от числа серий
i~Poiss(λi) => Σi~Pois(Σλi) - пуассоновское
λ - характеризует интенсивность потока событий
EΣi=Σλi – суммарная интенсивность нескольких потоков
Слайд 11ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ
Свойства нормального распределения:
~N(μ;2)
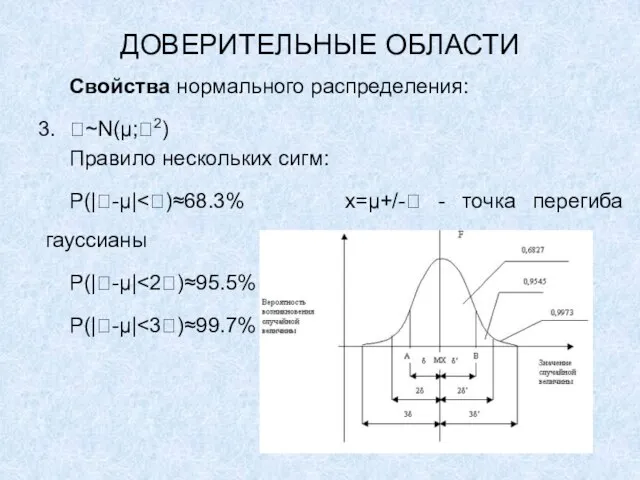
Правило нескольких сигм:
P(|-μ|<)≈68.3% x=μ+/- - точка перегиба гауссианы
P(|-μ|<2)≈95.5%
P(|-μ|<3)≈99.7%
Слайд 12ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, LN
Def ~LN(μ;2) – логнормальное распределение с параметром сдвига μ и
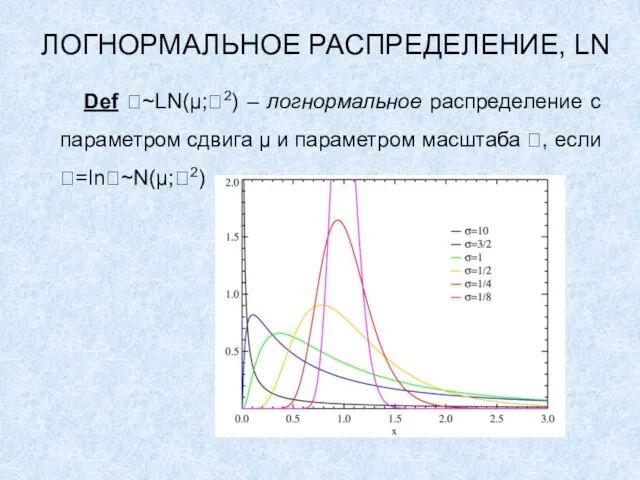
параметром масштаба , если =ln~N(μ;2)
Слайд 13ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, LN
Плотность логнормального распределения
Рассмотрим ~LN(0;1) <=> ~N(0;1)

Слайд 14ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, LN
Плотность логнормального распределения
~LN(0;1) <=> ~N(0;1)
~LN(μ;2) <=> ~N(μ;2)
Докажите, используя линейность нормального

закона
Слайд 15ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, LN
Свойства логнормального распределения
Докажите свойства (начните со случая ~LN(0;1) )

Слайд 16РАСПРЕДЕЛЕНИЕ Коши, С
Def 1, 2 ~N(0;1) => =1/2~C(0;1) – стандартное распределение Коши
Def
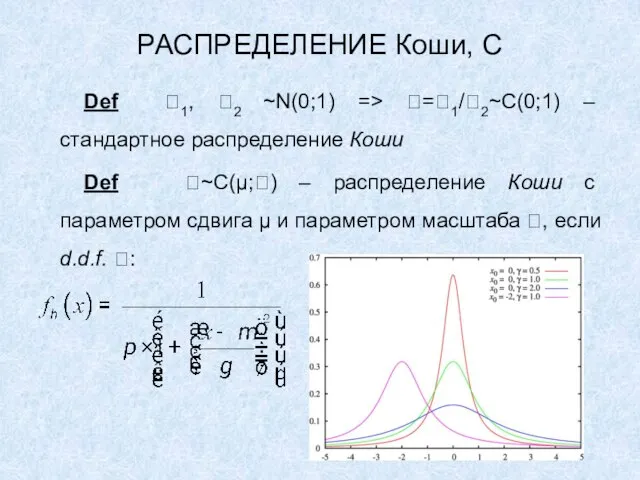
~C(μ;) – распределение Коши с параметром сдвига μ и параметром масштаба , если d.d.f. :
Слайд 17РАСПРЕДЕЛЕНИЕ Коши, С
Свойства распределения Коши:
~C(μ;)
Mo=Me=μ
Не существует ни одного момента!
( в т.ч.

E, D, As, Ex - не определены)
~C(μ;) => a+b~C(aμ+b;a)
i~C(0;1) i.i.d. => (Σi)/n ~ C(0;1)
Докажите свойства 1. и 3.
Слайд 18ГАММА-РАСПРЕДЕЛЕНИЕ, Γ
Def ~Г(k;) – Гамма-распределение с параметром формы k и параметром масштаба
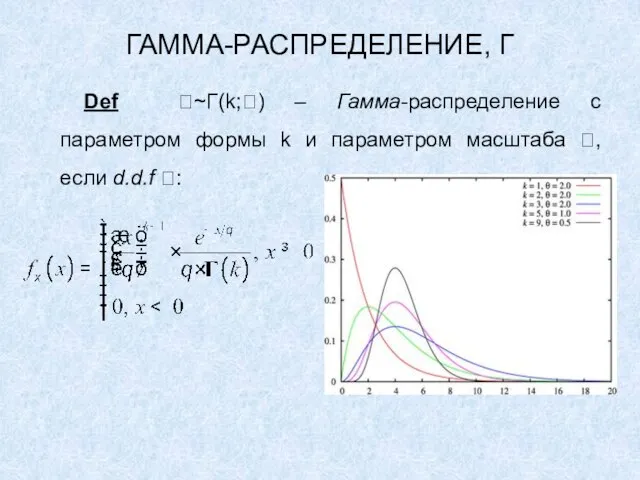
, если d.d.f :
Слайд 19ГАММА-РАСПРЕДЕЛЕНИЕ, Γ
Свойства Гамма-распределения:
Докажите свойства 1.-3. ,6. и 8.
(для 1. и 2. используйте

индукцию и свойство 7.)
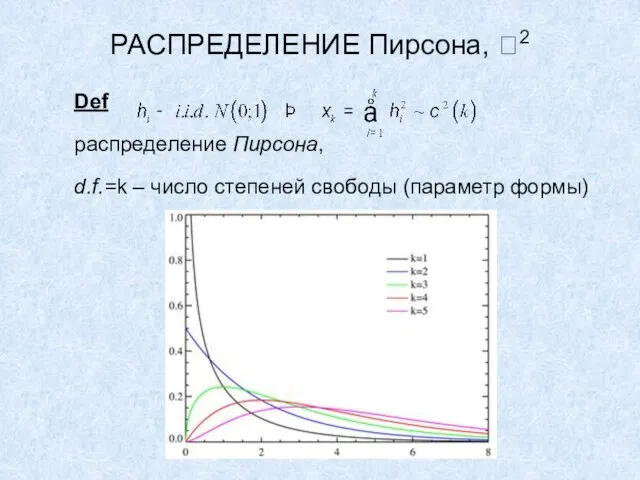
Слайд 20РАСПРЕДЕЛЕНИЕ Пирсона, 2
Def
распределение Пирсона,
d.f.=k – число степеней свободы (параметр формы)
Слайд 21РАСПРЕДЕЛЕНИЕ Пирсона, 2
Плотность распределения 2(1)
Рассмотрим ~N(0;1) <=> =2~2(1)

Слайд 22РАСПРЕДЕЛЕНИЕ Пирсона, 2
Плотность распределения 2(1)
Рассмотрим ~N(0;1) <=> =2~2(1)

Слайд 23РАСПРЕДЕЛЕНИЕ Пирсона, 2
Плотность распределения 2(1)
Рассмотрим ~N(0;1) <=> =2~2(1)

Слайд 24РАСПРЕДЕЛЕНИЕ Пирсона, 2
Свойства распределения 2(k)

Слайд 25РАСПРЕДЕЛЕНИЕ Пирсона, 2
Свойства распределения 2(k)
Все свойства (кроме 8.) – вытекают из двух:

Слайд 26РАСПРЕДЕЛЕНИЕ Пирсона, 2
Свойства распределения 2(k)
Прямое доказательство:
Докажите напрямую свойства 2., 3., 6.

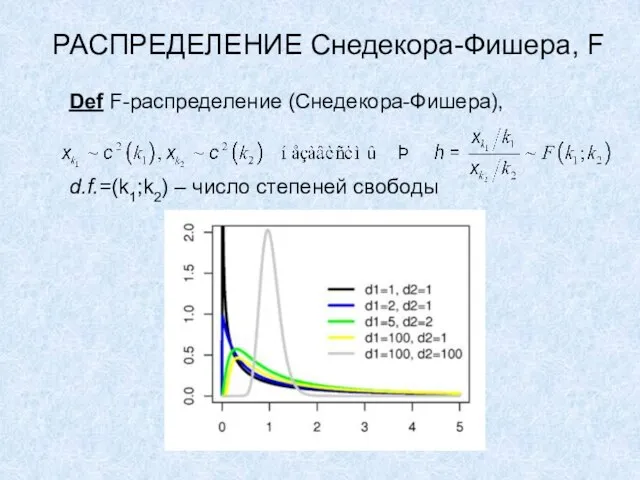
Слайд 27РАСПРЕДЕЛЕНИЕ Снедекора-Фишера, F
Def F-распределение (Снедекора-Фишера),
d.f.=(k1;k2) – число степеней свободы
Слайд 28РАСПРЕДЕЛЕНИЕ Снедекора-Фишера, F
Свойства F-распределения (Снедекора-Фишера)
Докажите свойства 3.-5.

Слайд 29РАСПРЕДЕЛЕНИЕ Стьюдента, St
Def распределение Стьюдента с d.f.=k (параметр формы):

Слайд 30РАСПРЕДЕЛЕНИЕ Стьюдента, St
Def распределение Стьюдента с d.f.=k (параметр формы):

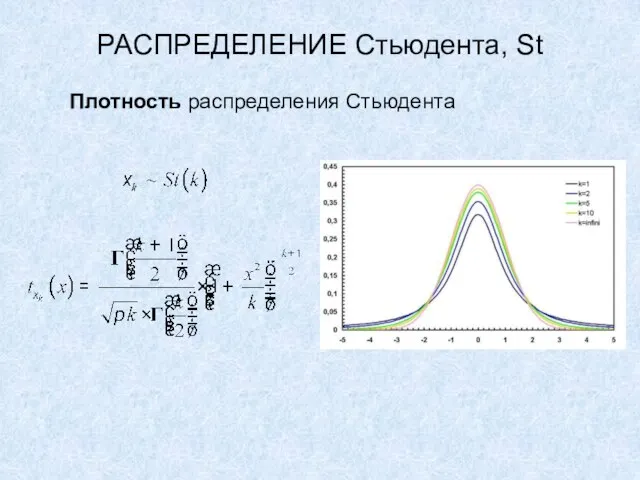
Слайд 31РАСПРЕДЕЛЕНИЕ Стьюдента, St
Плотность распределения Стьюдента
Слайд 32РАСПРЕДЕЛЕНИЕ Стьюдента, St
Свойства распределения St(k)
Докажите свойства 4.-7.
































 Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит
Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит NXP semiconductors, Москва. Краткий обзор
NXP semiconductors, Москва. Краткий обзор Однофазный TIG-инвертор
Однофазный TIG-инвертор Індекси цін у будівництві
Індекси цін у будівництві Банки и банковская система РФ. Тест
Банки и банковская система РФ. Тест Прикладной Тайм-менеджмент для программистов
Прикладной Тайм-менеджмент для программистов ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет
ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет Кабинет министров
Кабинет министров Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: +
Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: + Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки
Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки Сессия Госконтроль 2.0: образ будущего
Сессия Госконтроль 2.0: образ будущего Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Перпендикуляр и наклонные
Перпендикуляр и наклонные Однородные члены предложения
Однородные члены предложения Предмет, метод, источники и принципы Трудового права
Предмет, метод, источники и принципы Трудового права Поэты Ставрополья о родном крае и о природе родного края
Поэты Ставрополья о родном крае и о природе родного края Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр
Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр Обзор на персонажа
Обзор на персонажа ВКР: Действительный цикл машины МВВ6 - 1 -2
ВКР: Действительный цикл машины МВВ6 - 1 -2 15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом).
15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом). Правила наложения жгутов повязок и шин
Правила наложения жгутов повязок и шин Вальдорфская система образования
Вальдорфская система образования Social Ecology Sustainable Development
Social Ecology Sustainable Development  Ваш профессиональный маршрут
Ваш профессиональный маршрут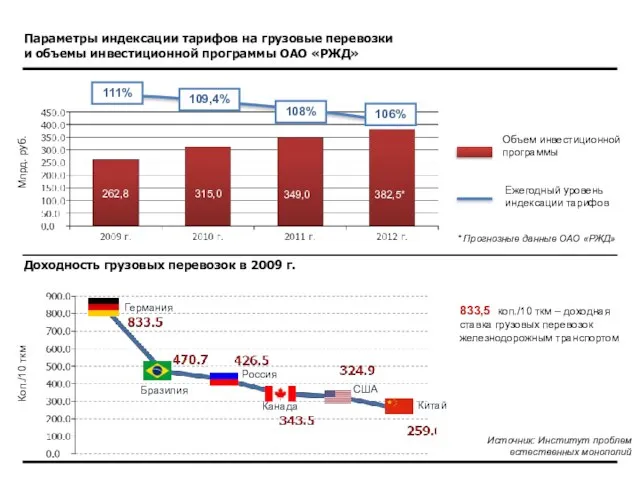 Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД»
Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД» Концепция воспитательной системы
Концепция воспитательной системы Технология создания и редактирования изображений в векторном редакторе
Технология создания и редактирования изображений в векторном редакторе Презентация на тему Использования краеведческого материала в образовательном процессе
Презентация на тему Использования краеведческого материала в образовательном процессе