Слайд 2Ударное взаимодействие тел
Закон сохранения механической энергии и закон сохранения импульса позволяют находить

решения механических задач в тех случаях, когда неизвестны действующие силы.
Примером такого рода задач является ударное взаимодействие тел.
Слайд 3Определение удара
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого

их скорости испытывают значительные изменения.
Слайд 4Применение законов сохранения энергии и импульса
Во время столкновения тел между ними действуют

кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
Слайд 5Абсолютно упругий удар
Абсолютно упругий удар - столкновение, при котором сохраняется механическая энергия

системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
Слайд 6Пример абсолютно упругого столкновения
Простым примером абсолютно упругого столкновения может быть центральный удар

двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Слайд 7Центральный удар
Центральный удар шаров - соударение, при котором скорости шаров до и

после удара направлены по линии центров.
Слайд 8Применение закона сохранения механической энергии
В общем случае массы m1 и m2 соударяющихся

шаров могут быть неодинаковыми.
Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2=0, u1 и u2 – скорости шаров после столкновения.
Слайд 9Применение закона сохранения импульса
Закон сохранения импульса для проекций скоростей на координатную

ось, направленную по скорости движения первого шара до удара, записывается в виде:
m1υ1=m1u1+m2u2.








 Исламское искусство в архитектуре Иерусалима
Исламское искусство в архитектуре Иерусалима Что такое море?
Что такое море? Агрессивность
Агрессивность Естествознание 5 класс тема Сбор и запись данных презентация (2)
Естествознание 5 класс тема Сбор и запись данных презентация (2) Машиностроительные материалы
Машиностроительные материалы Prezentatsia_Axyonova_S_O
Prezentatsia_Axyonova_S_O Культура Древней Греции
Культура Древней Греции  Презентация на тему Seasons of year and days of the week
Презентация на тему Seasons of year and days of the week  Jim Carrey (Amina)
Jim Carrey (Amina) BRITISH POETS
BRITISH POETS «Модели самоопределения учащихся основной школы в системе дополнительного и общего образования»
«Модели самоопределения учащихся основной школы в системе дополнительного и общего образования» Профиль. Образование. Карьера
Профиль. Образование. Карьера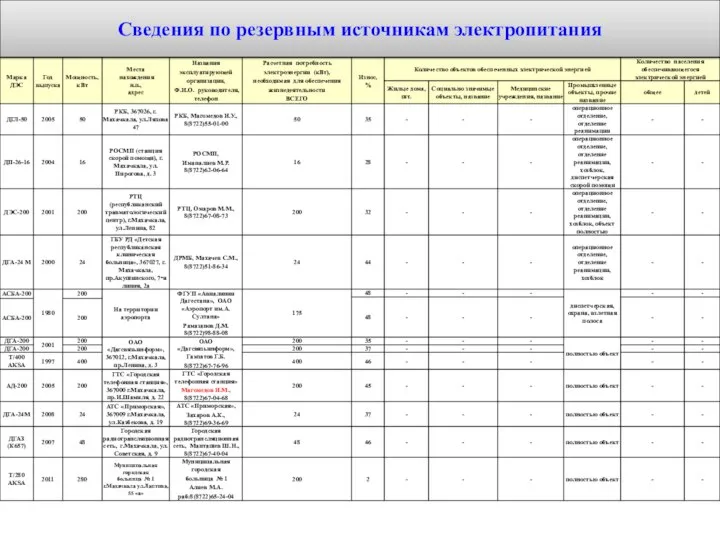 Сведения по резервным источникам электропитания
Сведения по резервным источникам электропитания Священное Писание - «перевод нового мира»или как нас обманывают Свидетели Иеговы
Священное Писание - «перевод нового мира»или как нас обманывают Свидетели Иеговы Огонь, вода, газ.
Огонь, вода, газ. 9260cbe975e6b77e67b1d7481dbedd76
9260cbe975e6b77e67b1d7481dbedd76 Спортивные площадки
Спортивные площадки Ситуация с отоплением и горячим водоснабжением в Мурманске
Ситуация с отоплением и горячим водоснабжением в Мурманске Эмоции а посте. Урок 5
Эмоции а посте. Урок 5 Муфта сцепления
Муфта сцепления Сталь Шмаков Из цикла «Педагоги Новосибирска »
Сталь Шмаков Из цикла «Педагоги Новосибирска » Учебный курс Введение в параллельные алгоритмы
Учебный курс Введение в параллельные алгоритмы Театр осенних миниатюр
Театр осенних миниатюр Щепа. Тиснение и резьба по бересте
Щепа. Тиснение и резьба по бересте Викторина "Знайка в мире русского языка"
Викторина "Знайка в мире русского языка" Устный счет в пределах 10
Устный счет в пределах 10 Сучасна релігійна ситуація в Україні
Сучасна релігійна ситуація в Україні Эндоскопические методы в диагностике и лечении ЖКК из верхних отделов ПВТ Докладчик староста СНК Лобастов К.В.
Эндоскопические методы в диагностике и лечении ЖКК из верхних отделов ПВТ Докладчик староста СНК Лобастов К.В.