Содержание
- 2. Модель производственной программы (краткосрочная) 1. Постановка задачи ♦
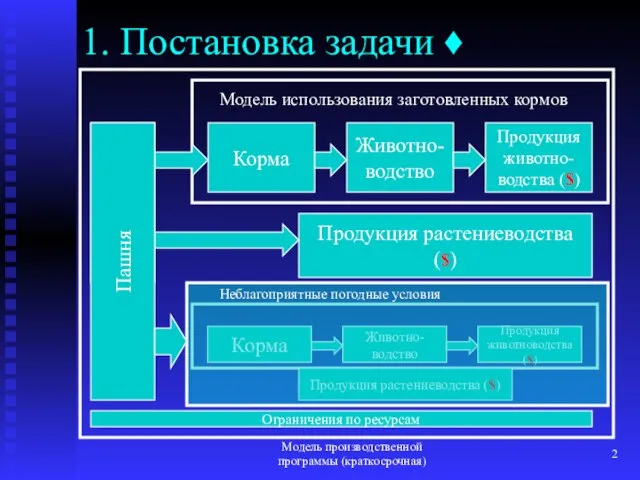
- 3. Модель производственной программы (краткосрочная) 1. Постановка задачи Определить основные показатели плана производственной деятельности сельскохозяйственного предприятия на
- 4. Модель производственной программы (краткосрочная) 1. Учёт рисков ♦ Моделирование двухэтапного процесса принятия решений (см. лекцию 2,
- 5. Модель производственной программы (краткосрочная) 1. Обоснование субмоделей II этапа Классический подход (В.А. Кардаш): по многолетним данным
- 6. Модель производственной программы (краткосрочная) 1. Обоснование субмоделей II этапа ♦ Рекомендуемый подход разрабатываются две субмодели: для
- 7. Модель производственной программы (краткосрочная) Если при неблагоприятных условиях допускается сокращение маточного поголовья, соответствующие переменные вводятся в
- 8. Модель производственной программы (краткосрочная) 2. Математическое представление модели ♦ Переменные субмодель апостериорного решения для погодных условий
- 9. Модель производственной программы (краткосрочная) 2. Математическое представление модели ♦ Ограничения субмодели априорного решения По наличию земельных
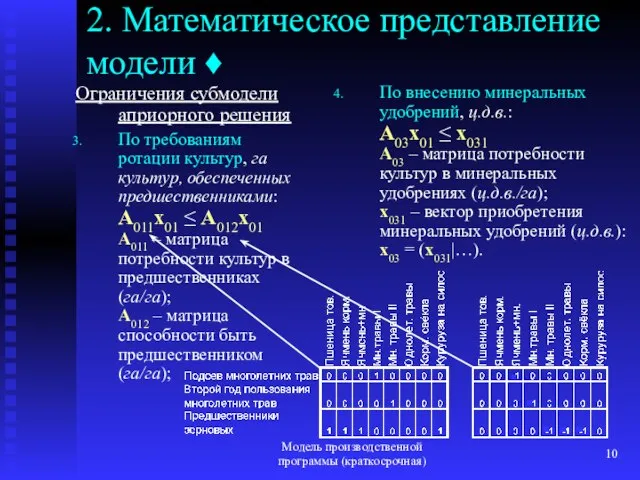
- 10. Модель производственной программы (краткосрочная) 2. Математическое представление модели ♦ Ограничения субмодели априорного решения По требованиям ротации
- 11. Модель производственной программы (краткосрочная) 2. Ограничения II этапа Баланс продукции растениеводства, ц An1x01 ≥ An2xn1+An3xn2 An1
- 12. Модель производственной программы (краткосрочная) 2. Ограничения II этапа Откорм скота и птицы, кормо-лет откорма a04x02j ≤
- 13. Модель производственной программы (краткосрочная) 2. Ограничения II этапа Баланс кормов, ц.к.е. A0Axn2 ≥ A0Bxn3 A0A –
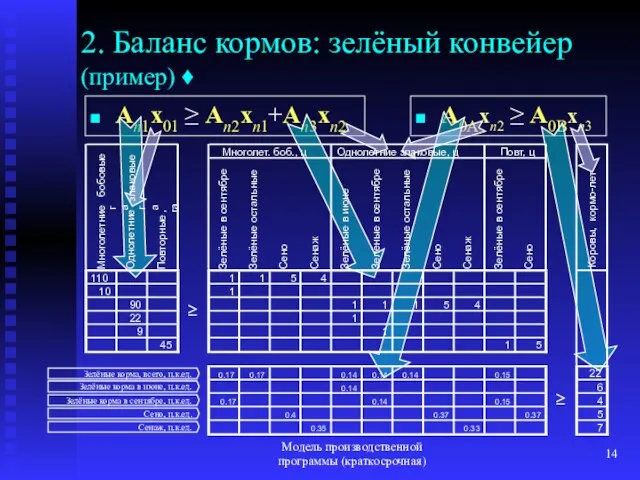
- 14. Модель производственной программы (краткосрочная) 2. Баланс кормов: зелёный конвейер (пример) ♦ An1x01 ≥ An2xn1+An3xn2 A0Axn2 ≥
- 15. 2. Ограничения II этапа На финансирование производственных затрат, тыс.руб. an4x01+a0Cx03 +an5xn2 +a0Dxn3 ≤ xn41+ bn1 7.
- 16. 2. Ограничения II этапа На покрытие убытков, тыс.руб.: xn5 – xn6 ≤ xn42 (xn41, xn42) =
- 17. Модель производственной программы (краткосрочная) 2. Математическое представление модели ♦ Полные затраты (тыс. руб.) xn5 ≥ an6x01+a0Ex03
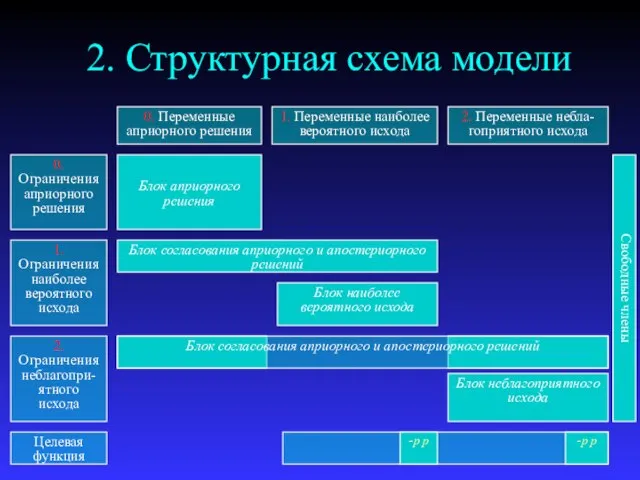
- 18. 2. Структурная схема модели 0. Переменные априорного решения 1. Переменные наиболее вероятного исхода 2. Переменные небла-гоприятного
- 19. 3. Разработка числовой модели: система переменных x01 — площади посевов: все фактически выращиваемые культуры; районированные культуры,
- 20. Модель производственной программы (краткосрочная) 3. Разработка числовой модели: система переменных xn1 — реализация продукции: вся фактически
- 21. Модель производственной программы (краткосрочная) 3. Разработка числовой модели: система переменных xn3 — содержание животных: как минимум
- 22. Модель производственной программы (краткосрочная) 3. Разработка числовой модели b01 – наличие земельных угодий: по плану землепользования
- 23. Модель производственной программы (краткосрочная) 3. Разработка числовой модели A03 – потребность культур в минеральных удобрениях: согласно
- 24. Модель производственной программы (краткосрочная) 3. Разработка числовой модели a04, a05 –число кормо-лет откорма (минимальное и максимальное)
- 25. Модель производственной программы (краткосрочная) 3. Разработка числовой модели A07 – внесение навоза: согласно технологическим картам; согласно
- 26. Модель производственной программы (краткосрочная) 3. Разработка числовой модели A0B – потребность в кормах согласно рациону: в
- 27. Модель производственной программы (краткосрочная) 3. Разработка числовой модели a0E – затраты на ресурсы, расходуемые при посеве:
- 28. Модель производственной программы (краткосрочная) 3. Разработка числовой модели a0F – затраты на реализацию продукции: по фактическим
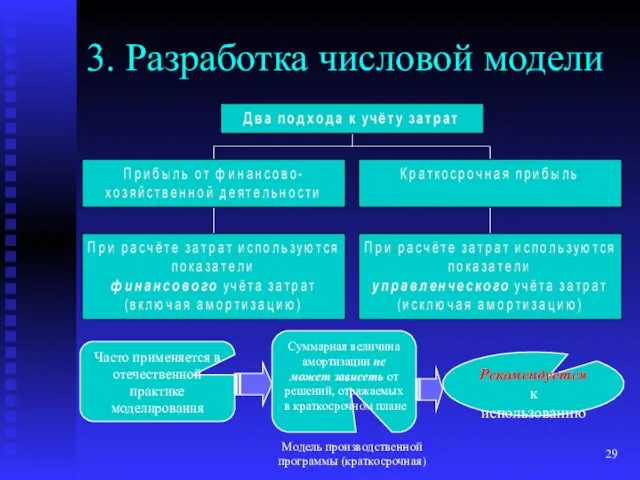
- 29. Модель производственной программы (краткосрочная) 3. Разработка числовой модели Рекомендуется к использованию Часто применяется в отечественной практике
- 30. Модель производственной программы (краткосрочная) 3. Разработка числовой модели bn1 – объём собственных оборотных средств: по прогнозному
- 31. Модель производственной программы (краткосрочная) 3. Разработка числовой модели pn – весовой коэффициент погодных условий: p2 =
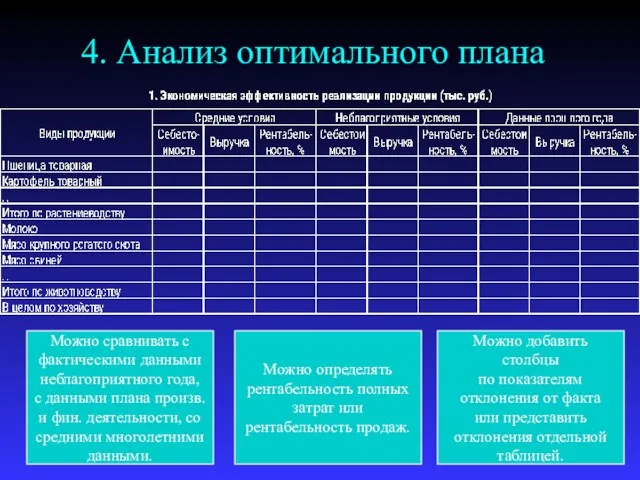
- 32. 4. Анализ оптимального плана Можно сравнивать с фактическими данными неблагоприятного года, с данными плана произв. и
- 33. 4. Анализ оптимального плана Можно сравнивать с фактическими данными неблагоприятного года, с данными плана произв. и
- 34. Модель производственной программы (краткосрочная) 4. Анализ оптимального плана Расчёт затрат на товарную продукцию Можно разносить затраты
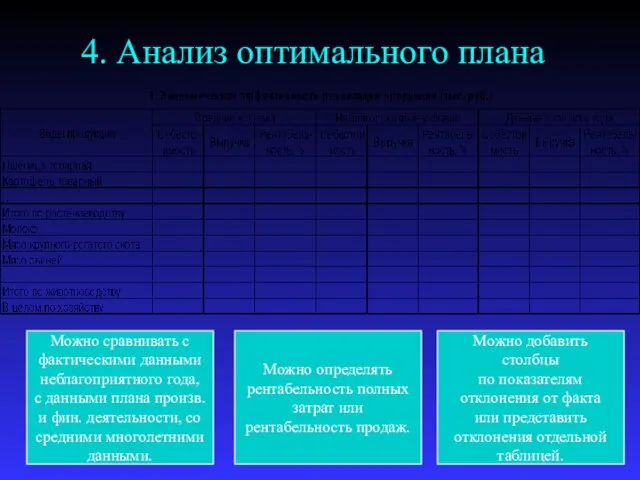
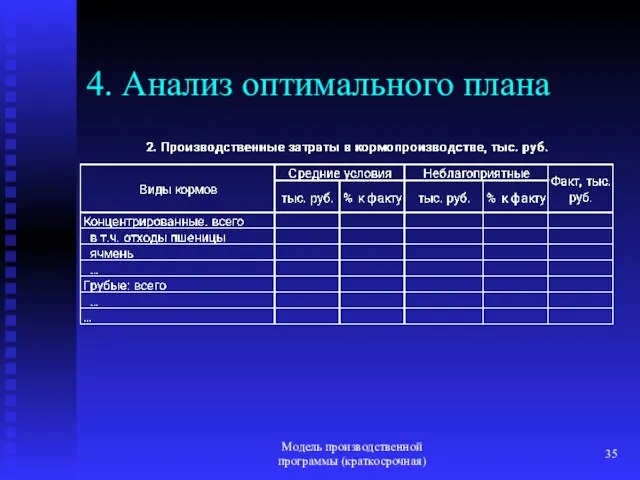
- 35. Модель производственной программы (краткосрочная) 4. Анализ оптимального плана
- 36. Модель производственной программы (краткосрочная) 4. Анализ оптимального плана
- 37. Модель производственной программы (краткосрочная) 4. Анализ оптимального плана Таблица составляется для каждого исхода погодных условий
- 38. Модель производственной программы (краткосрочная) 4. Анализ оптимального плана Таблица составляется для каждого исхода погодных условий
- 39. Модель производственной программы (краткосрочная) 4. Анализ оптимального плана Таблица составляется для каждого исхода погодных условий
- 40. Модель производственной программы (краткосрочная) 4. Анализ оптимального плана Таблица составляется для каждого исхода погодных условий
- 41. Модель производственной программы (краткосрочная) 4. Анализ оптимального плана Таблица 6 составляется для каждого исхода погодных условий
- 42. Модель производственной программы (краткосрочная) 4. Анализ оптимального плана Таблицы составляются для каждого исхода погодных условий
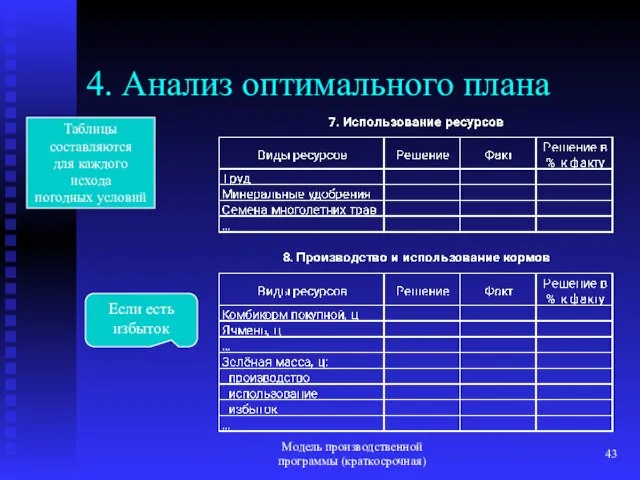
- 43. Модель производственной программы (краткосрочная) 4. Анализ оптимального плана Если есть избыток Таблицы составляются для каждого исхода
- 44. Модель производственной программы (краткосрочная) 4. Анализ оптимального плана Если есть избыток Таблицы составляются для каждого исхода
- 45. Модель производственной программы (краткосрочная) 4. При необходимости может быть выполнен анализ: объёмов реализации продукции в натуральном
- 46. Модель производственной программы (краткосрочная) 4. Анализ двойственных оценок: как в модели использования кормов, только по всем
- 47. Модель производственной программы (краткосрочная) 5. Эксплуатация модели Модель составляется и решается перед осенней посевной. Если к
- 48. Модель производственной программы (краткосрочная) 5. Эксплуатация модели Ограничения по ресурсам следует «включать» одно за другим по
- 49. Модель производственной программы (краткосрочная) 5. Эксплуатация модели Типичная ошибка – набор рационов, использованных в модели, не
- 50. Модель производственной программы (краткосрочная) 5. Эксплуатация модели Выбор «слишком неблагоприятного» исхода может вызвать: несовместность системы ограничений;
- 51. 6. Направления совершенствования модели Недостатки модели: Трудоёмкость определения коммерческой себестоимости продукции. Избыточное резервирование ресурсов на случай
- 52. 6. Направления совершенствования модели ♦ Недостатки модели: Не учитывается неравномерность потребности в ресурсах (особенно в оборотных
- 54. Скачать презентацию










































 AvB
AvB Презентация на тему Общественное движение при Александре 2
Презентация на тему Общественное движение при Александре 2  Электронные образовательные ресурсы: внедряем и используем
Электронные образовательные ресурсы: внедряем и используем Презентация на тему Все профессии важны, с математикой дружны
Презентация на тему Все профессии важны, с математикой дружны  Работа психолога с воспитателями
Работа психолога с воспитателями Настоящие отношения
Настоящие отношения Заблуждения о ценах
Заблуждения о ценах Святые земли Тотемской
Святые земли Тотемской ФАЙЛЫ и ПАПКИ
ФАЙЛЫ и ПАПКИ Химическая связь. Строение вещества
Химическая связь. Строение вещества Презентация на тему Городецкая роспись (2 класс)
Презентация на тему Городецкая роспись (2 класс) ВИМКОМ
ВИМКОМ Аудиторская компания «ПартнерГрупп»
Аудиторская компания «ПартнерГрупп» Основні напрямки соціалізації дітей дошкільного віку професор, доктор наук Бочаров Сергій Вікторович
Основні напрямки соціалізації дітей дошкільного віку професор, доктор наук Бочаров Сергій Вікторович Калашников Михаил Тимофеевич. Человек-легенда. Человек - эпоха
Калашников Михаил Тимофеевич. Человек-легенда. Человек - эпоха Школа кулинаров. 3 класс
Школа кулинаров. 3 класс Особенности обеспечения надежного контактирования ЭКБ при проведении климатических испытаний
Особенности обеспечения надежного контактирования ЭКБ при проведении климатических испытаний Знатоки Отечественной войны 1812 года
Знатоки Отечественной войны 1812 года Боевой листок
Боевой листок АНАЛИЗ ПОКАЗАТЕЛЕЙ ЗДОРОВЬЯ МАТЕРИ И РЕБЕНКА В УСЛОВИЯХ РЕФОРМИРОВАНИЯ СЛУЖБЫ РОДОВСПОМОЖЕНИЯ В РОССИИ В 2006-2011 гг.(ПО ДАННЫМ Ф
АНАЛИЗ ПОКАЗАТЕЛЕЙ ЗДОРОВЬЯ МАТЕРИ И РЕБЕНКА В УСЛОВИЯХ РЕФОРМИРОВАНИЯ СЛУЖБЫ РОДОВСПОМОЖЕНИЯ В РОССИИ В 2006-2011 гг.(ПО ДАННЫМ Ф Март. Математика. Море
Март. Математика. Море Возможные, новые федеральные территории России
Возможные, новые федеральные территории России Цифровое бессмертие. Нейросети и организм человека
Цифровое бессмертие. Нейросети и организм человека Латинская Америка в 19-20 веке
Латинская Америка в 19-20 веке Прием в 1 классы. Алгоритм действий родителей. Районные отделы образования
Прием в 1 классы. Алгоритм действий родителей. Районные отделы образования Урок природоведенияпо теме «Живые клетки»
Урок природоведенияпо теме «Живые клетки» Целевые рынки и политика фирмы
Целевые рынки и политика фирмы Презентация на тему Хождение за три моря
Презентация на тему Хождение за три моря