Тема урока «Свойство медианы равнобедренного треугольника»

1.Актуализация знаний.
2.Проверка домашнего задания.
3.Теорема о свойстве медианы равнобедренного треугольника
4. Физминутка.
5. Решение задач
6. Итог урока
7. Домашнее задание
План урока

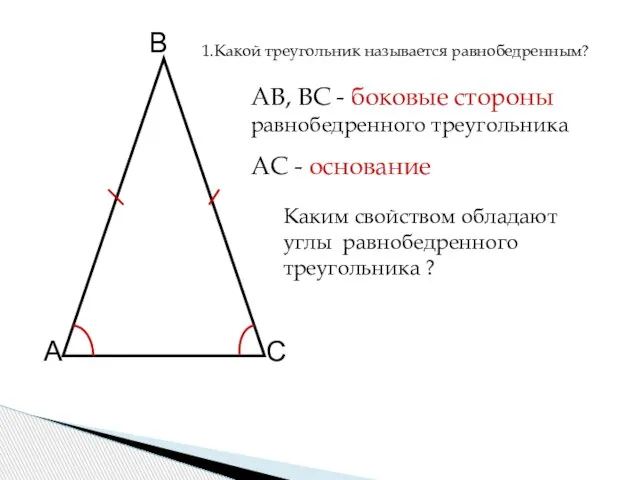
А
В
С
АВ, ВС - боковые стороны равнобедренного треугольника
АС - основание равнобедренного треугольника
Каким свойством обладают углы равнобедренного треугольника ?
1.Какой треугольник называется равнобедренным?
В

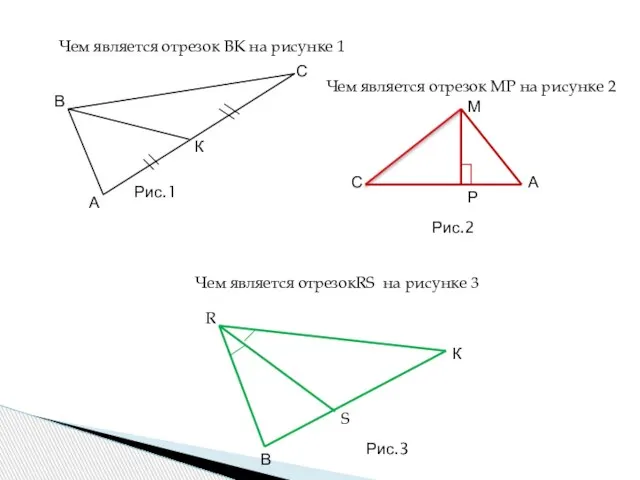
А
В
С
К
Рис.1
Чем является отрезок ВК на рисунке 1
Чем является отрезок МР на рисунке 2
М
Р
С
А
Чем является отрезокRS на рисунке 3
Рис.3
Рис.2
R
S
В
К

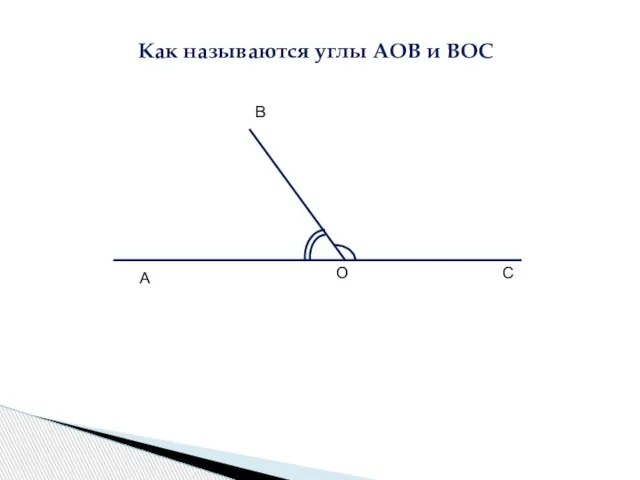
Как называются углы АОВ и ВОС
А
О
С
В

27.02.2012
Классная работа
Свойство медианы равнобедренного треугольника

А
В
СВ
С го треугольника
равно ДАНО: Δ АВС- равнобедренный,
АВ- основание, СD – медиана
ДОКАЗАТЬ: СД- биссектриса, высота
Из равенства треугольников следует <АСD = <ВСD , <АDС = <ВDС, значит СD – биссектриса.
<АDС и <ВDС – смежные и равны,
то они по 90˚ (прямые),
поэтому СD - высота
Теорема: в равнобедренном треугольнике медиана, проведенная к основанию является биссектрисой и высотой
А
В
С
D
ДОКАЗАТЕЛЬСТВО:
∆САD=∆CВD по Ι признаку равенства треугольников
АD = ВD, АС= СВ
<САD = <СВD,

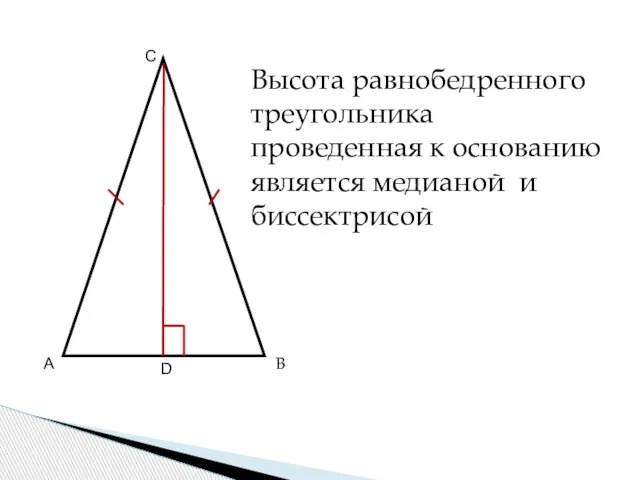
А
В
СВ
С го треугольника
А
В
С
D
Высота равнобедренного треугольника проведенная к основанию является медианой и биссектрисой

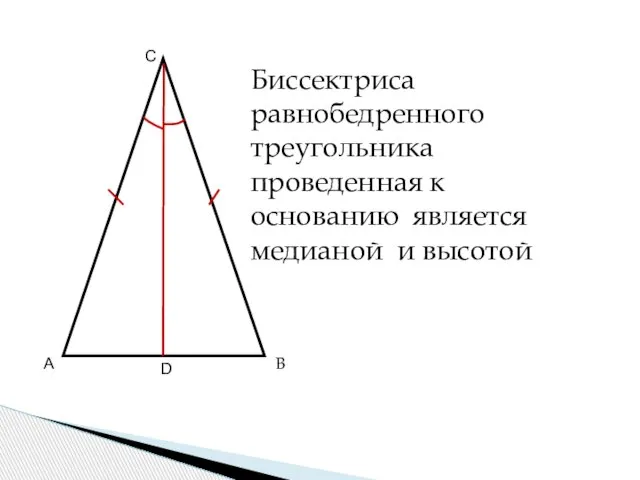
А
В
СВ
С го треугольника
А
В
С
D
Биссектриса равнобедренного треугольника проведенная к основанию является медианой и высотой

ФИЗМИНУТКА

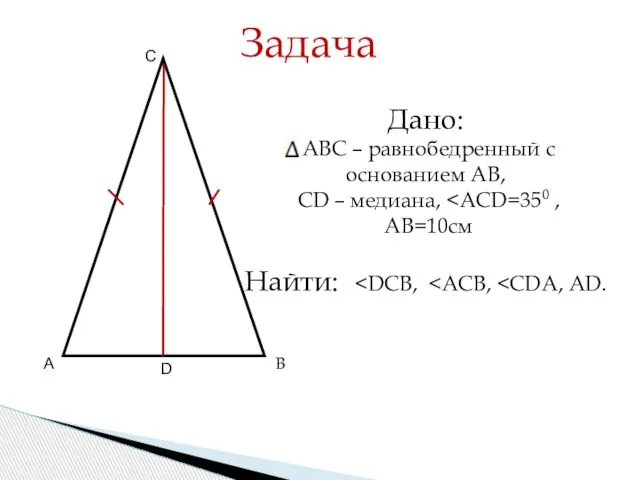
А
В
СВ
С го треугольника
А
В
С
D
Задача
Дано:
АВС – равнобедренный с основанием АВ,
СD – медиана, <АСD=350 ,
АВ=10см
Найти: