Содержание
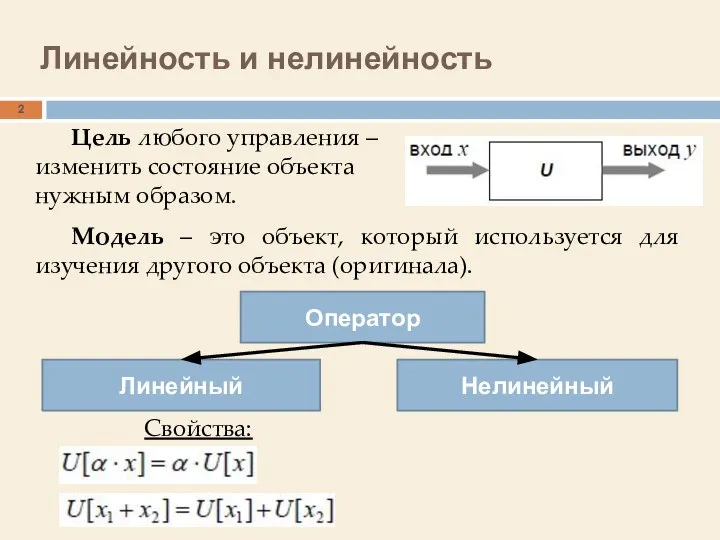
- 2. Линейность и нелинейность Цель любого управления – изменить состояние объекта нужным образом. Модель – это объект,
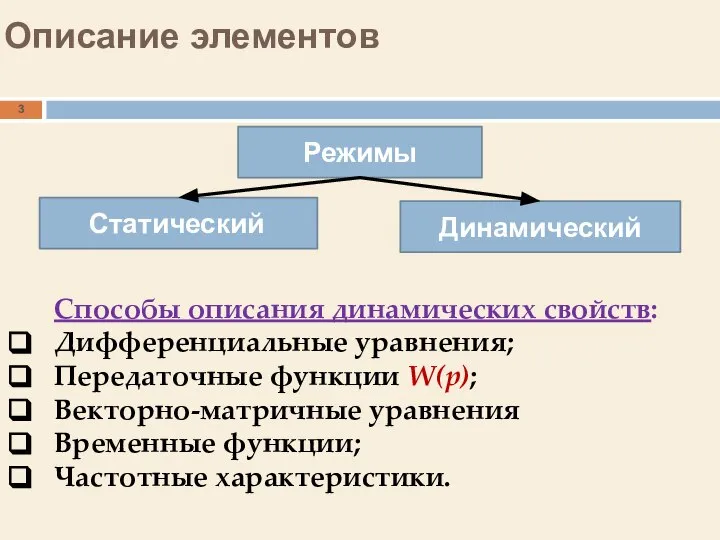
- 3. Описание элементов Способы описания динамических свойств: Дифференциальные уравнения; Передаточные функции W(p); Векторно-матричные уравнения Временные функции; Частотные
- 4. Дифференциальные уравнения Здесь: y(t) – временная функция выходного сигнала; x(t) – временная функция входного сигнала; y(j)(t)
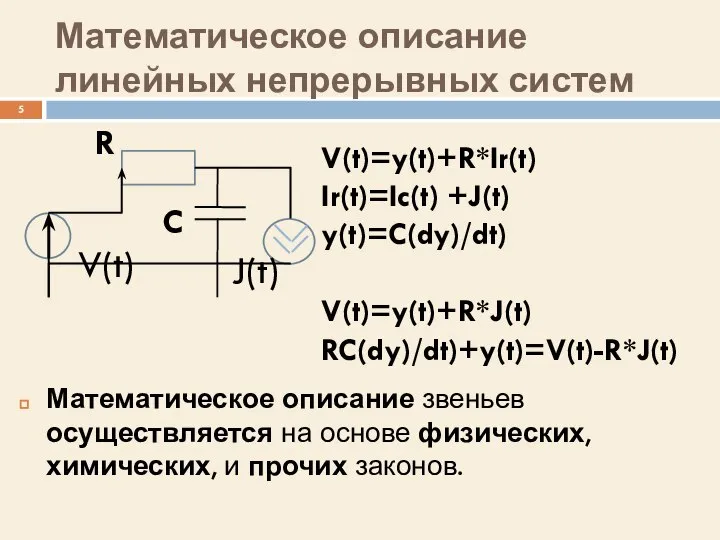
- 5. Математическое описание линейных непрерывных систем Математическое описание звеньев осуществляется на основе физических, химических, и прочих законов.
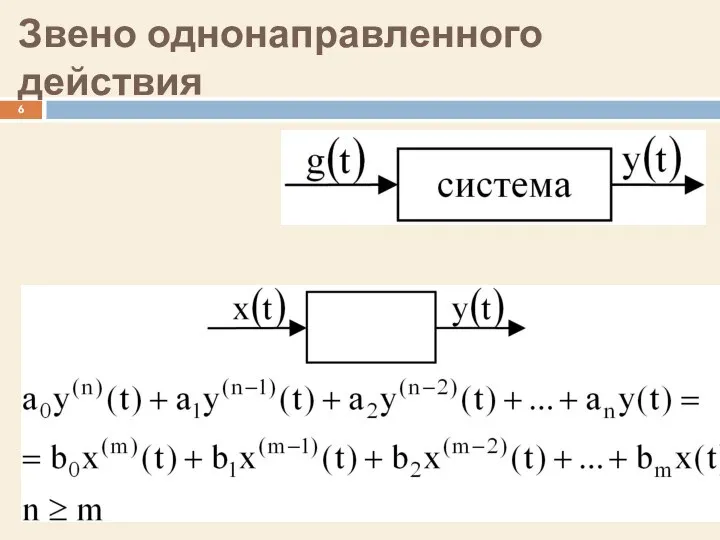
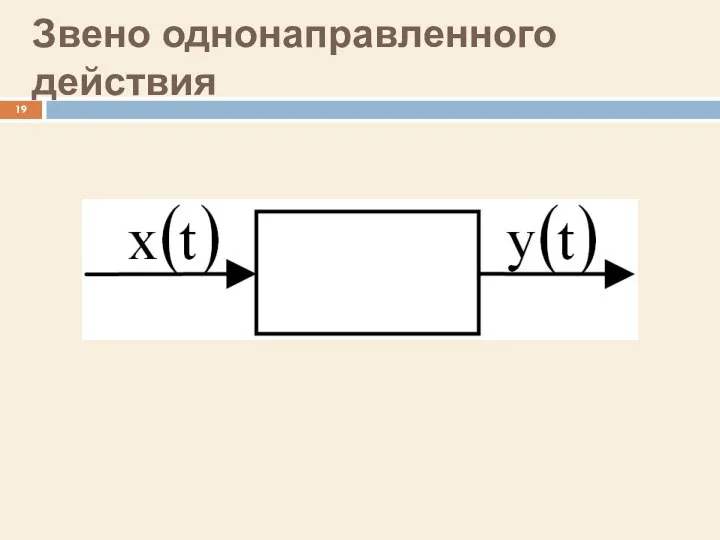
- 6. Звено однонаправленного действия
- 7. Преобразование Лапласа
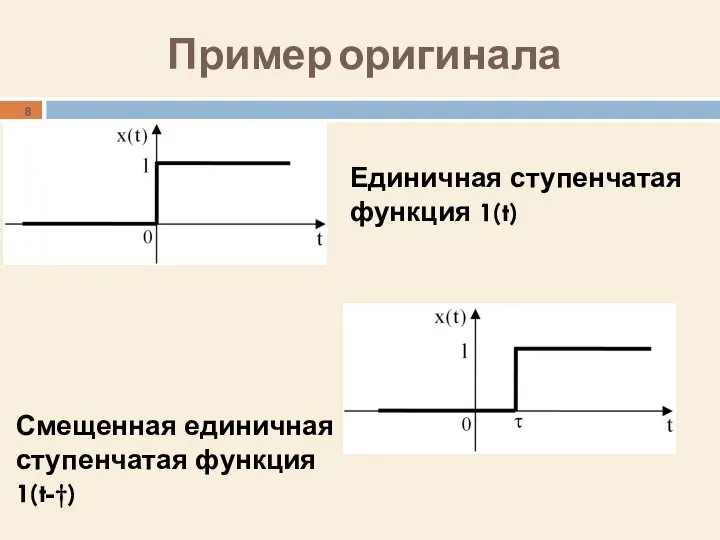
- 8. Пример оригинала Единичная ступенчатая функция 1(t) Смещенная единичная ступенчатая функция 1(t-†)
- 9. Преобразования Лапласа функций времени
- 10. Свойства преобразования Лапласа
- 11. Свойства преобразования Лапласа 2. Дифференцирование оригинала
- 12. Таблица оригиналов и изображений (обратное/прямое преобразование Лапласа)
- 13. Математическое описание в форме линейных дифференциальных уравнений
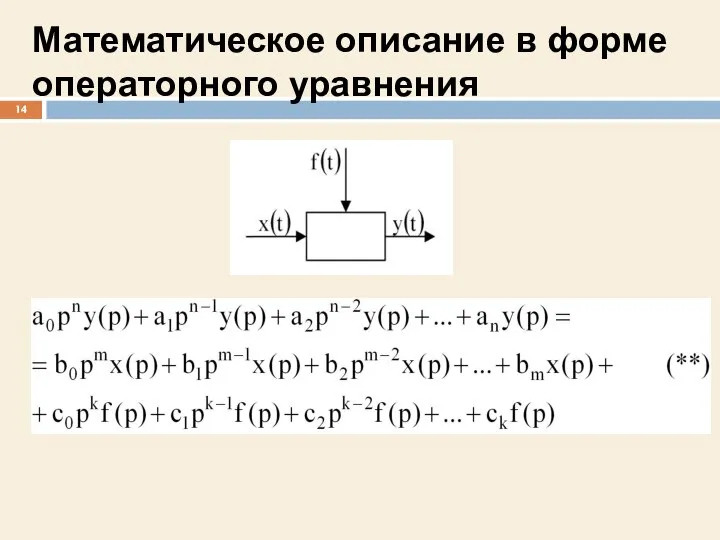
- 14. Математическое описание в форме операторного уравнения
- 15. Математическое описание в форме операторного уравнения
- 16. Математическое описание в форме операторного уравнения
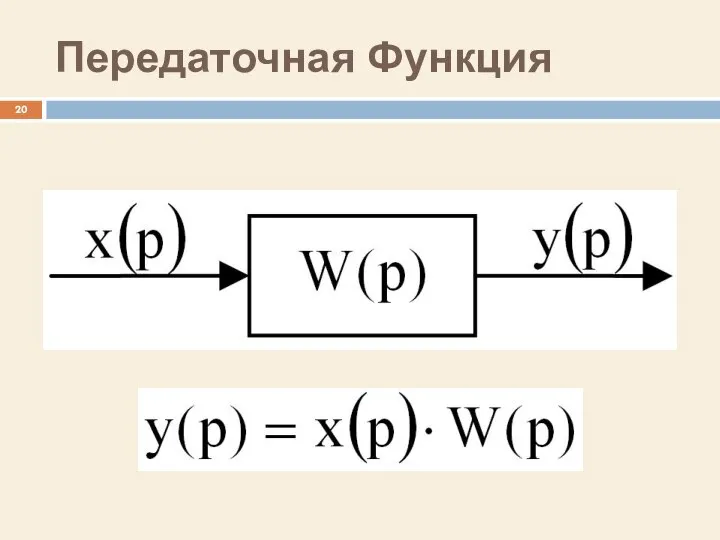
- 17. Передаточная Функция
- 18. Передаточная функция Передаточная функция W(p) есть отношение выходного сигнала к входному сигналу, представленное в операторной форме:
- 19. Звено однонаправленного действия
- 20. Передаточная Функция
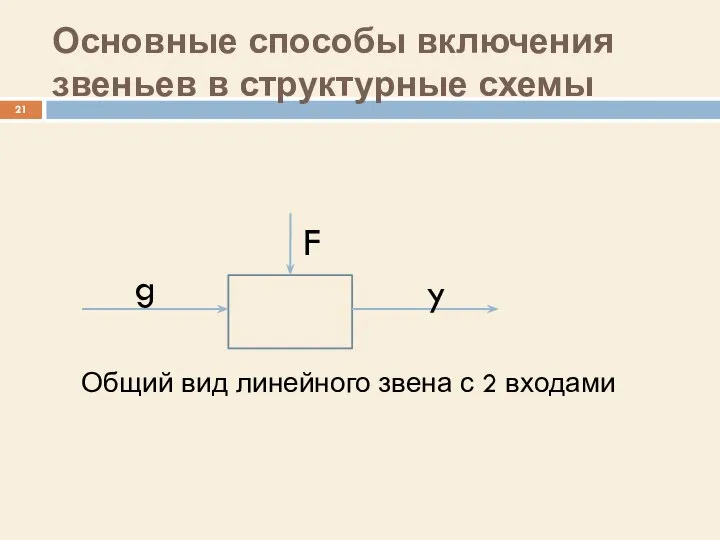
- 21. Основные способы включения звеньев в структурные схемы Общий вид линейного звена с 2 входами
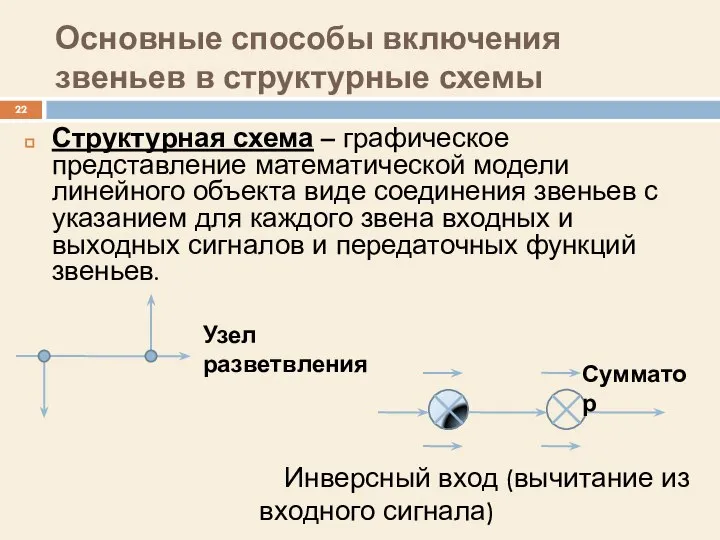
- 22. Основные способы включения звеньев в структурные схемы Инверсный вход (вычитание из входного сигнала) Структурная схема –
- 23. Основные способы соединения 1)Последовательное 2)Параллельное 3)Соединение с обратной связью
- 24. Последовательное соединение 1) Выход предыдущего звена, является входом последующего. G(t) W1 W2 W3
- 25. Последовательное соединение звеньев
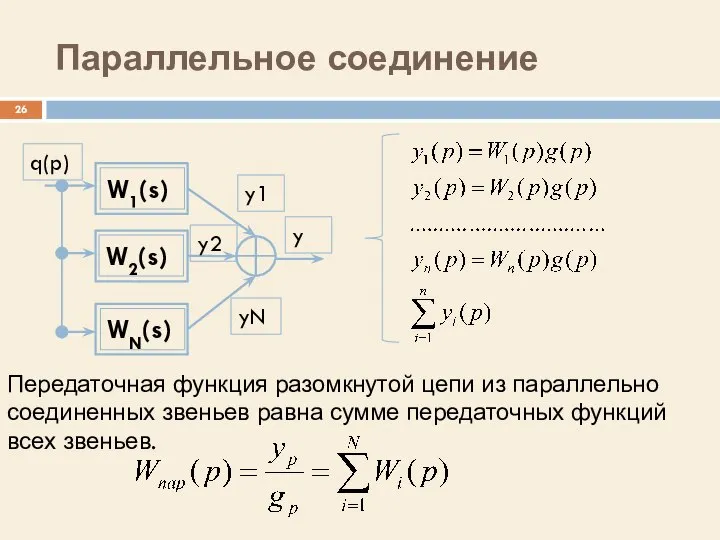
- 26. Параллельное соединение Передаточная функция разомкнутой цепи из параллельно соединенных звеньев равна сумме передаточных функций всех звеньев.
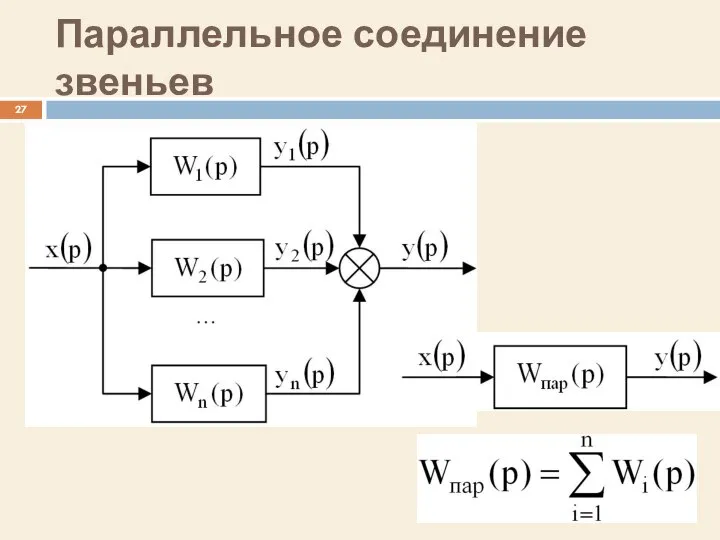
- 27. Параллельное соединение звеньев
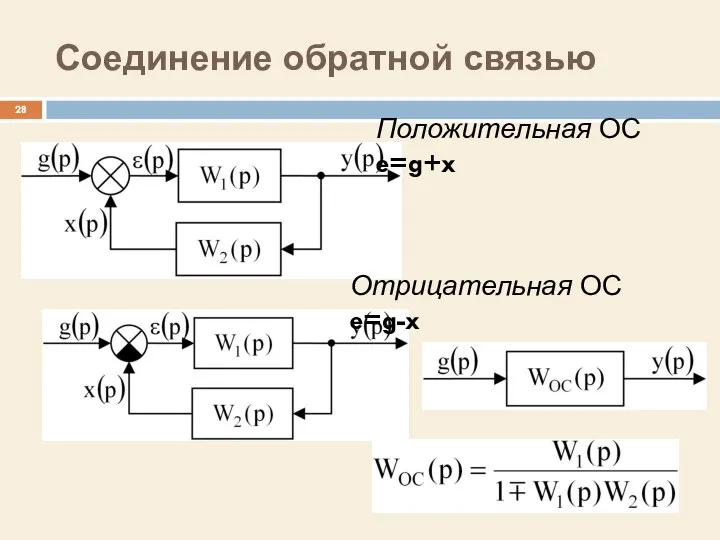
- 28. Соединение обратной связью Положительная ОС e=g+x Отрицательная ОС e=g-x
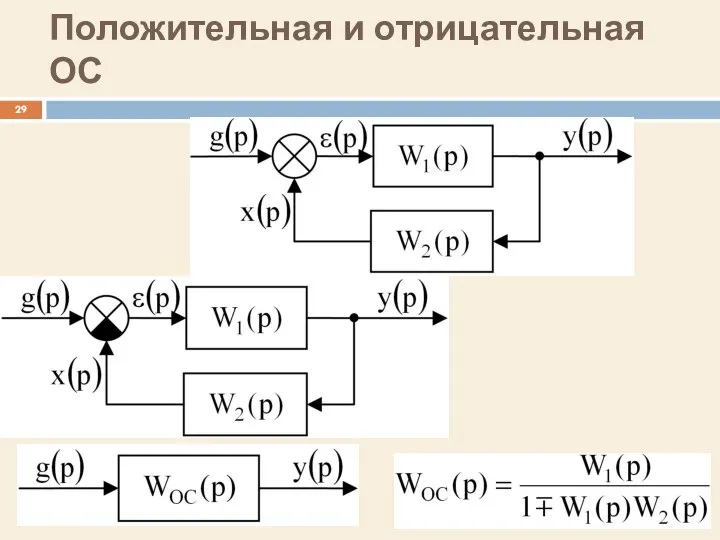
- 29. Положительная и отрицательная ОС
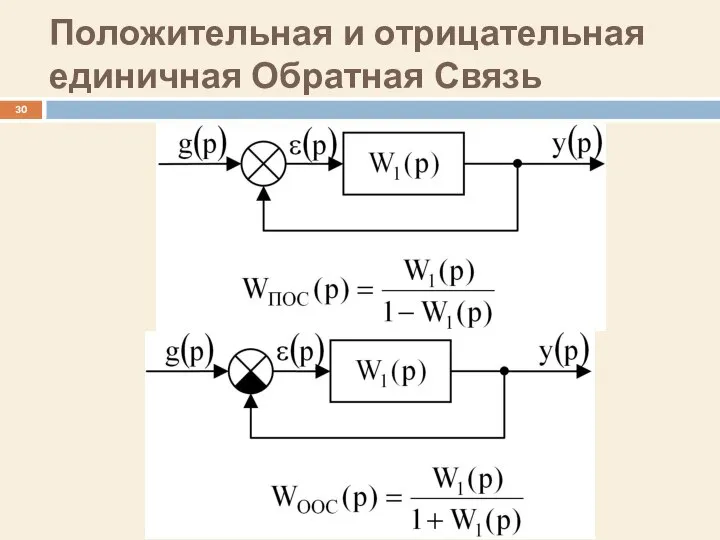
- 30. Положительная и отрицательная единичная Обратная Связь
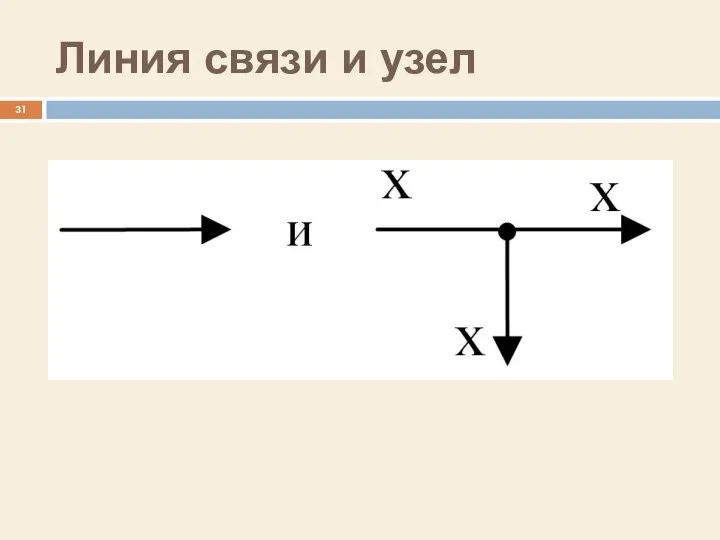
- 31. Линия связи и узел
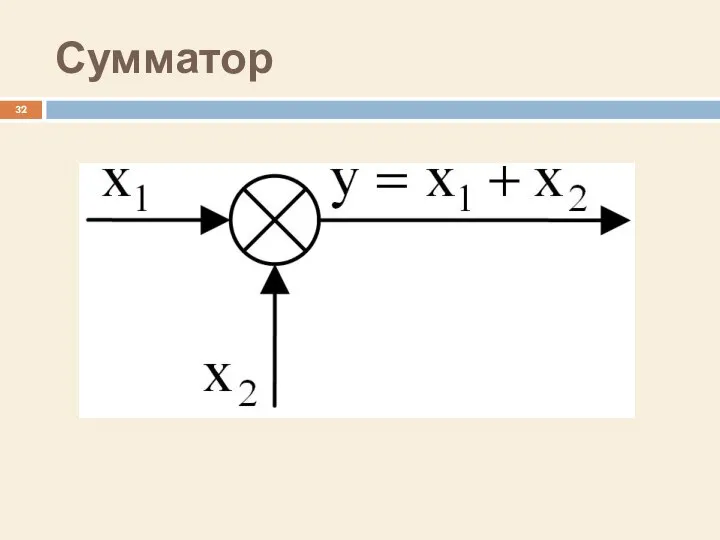
- 32. Сумматор
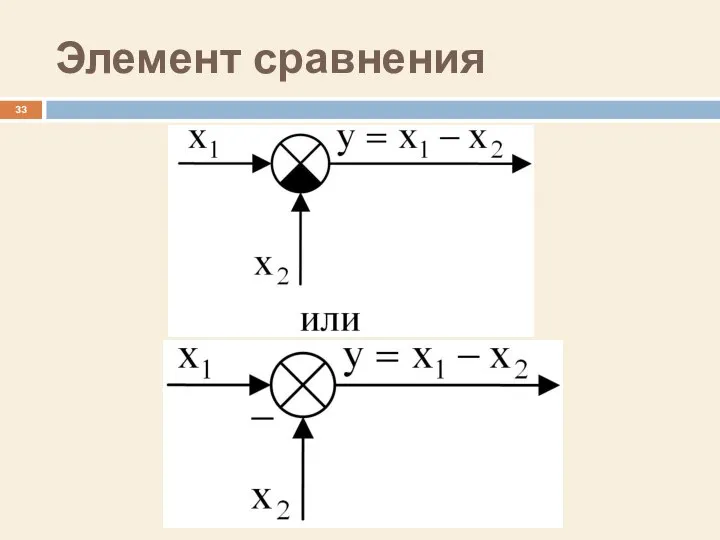
- 33. Элемент сравнения
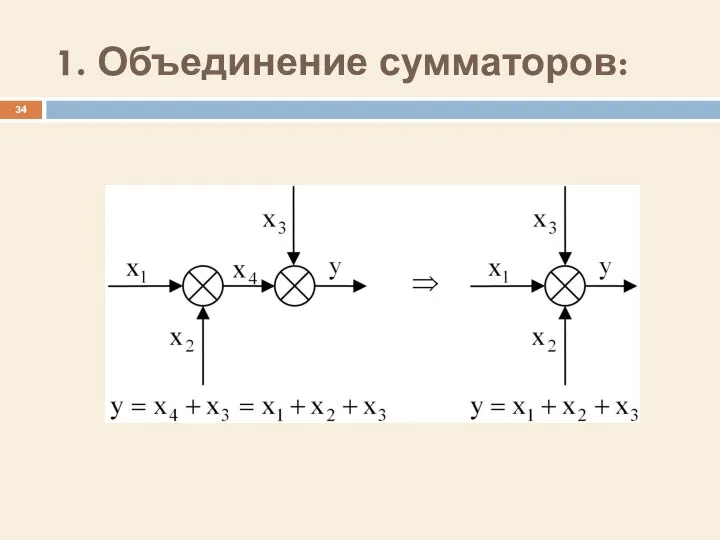
- 34. 1. Объединение сумматоров:
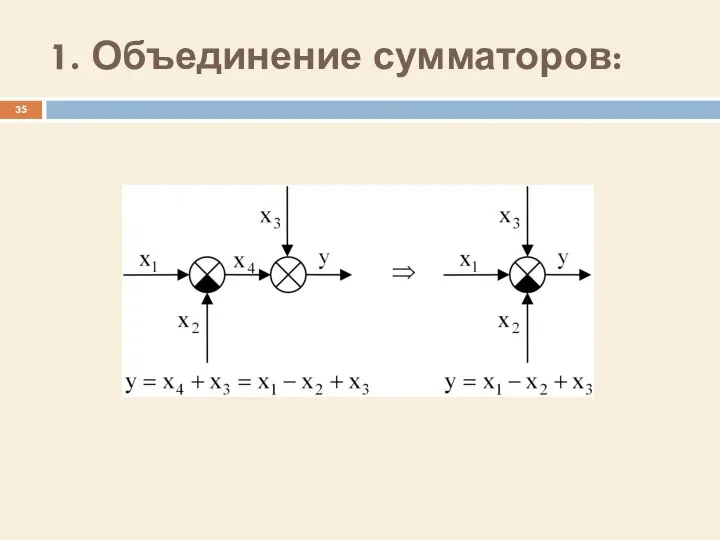
- 35. 1. Объединение сумматоров:
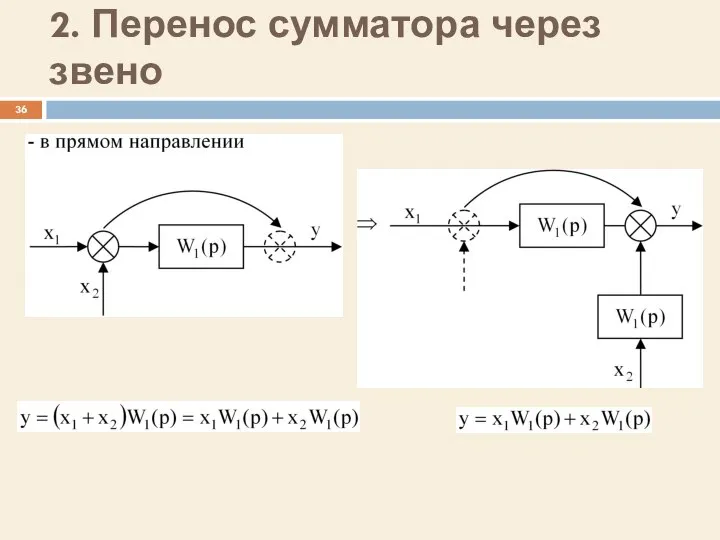
- 36. 2. Перенос сумматора через звено
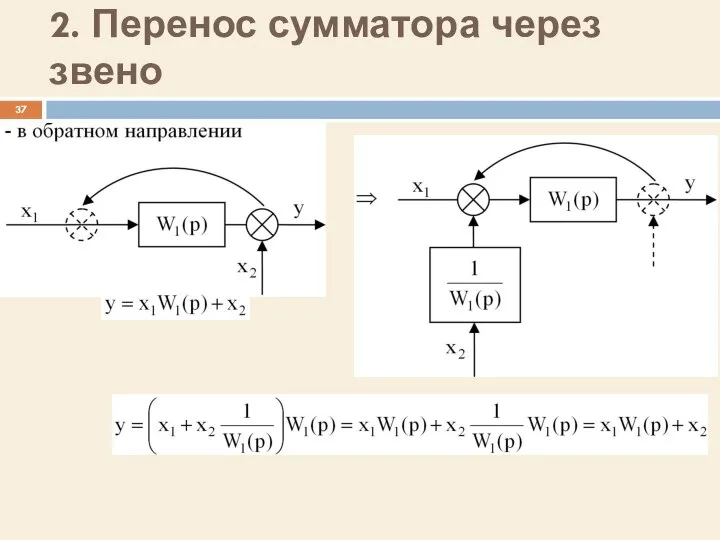
- 37. 2. Перенос сумматора через звено
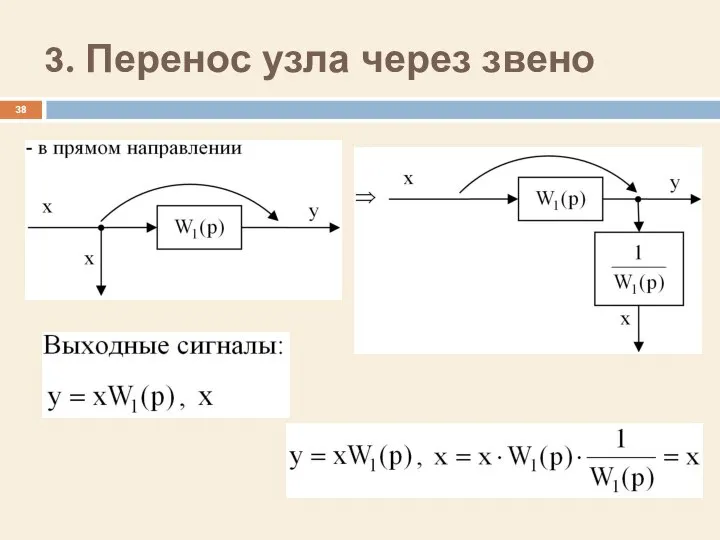
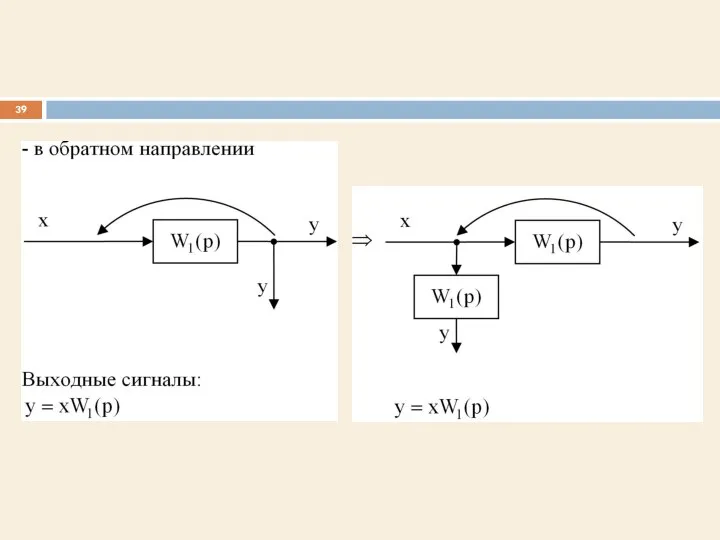
- 38. 3. Перенос узла через звено
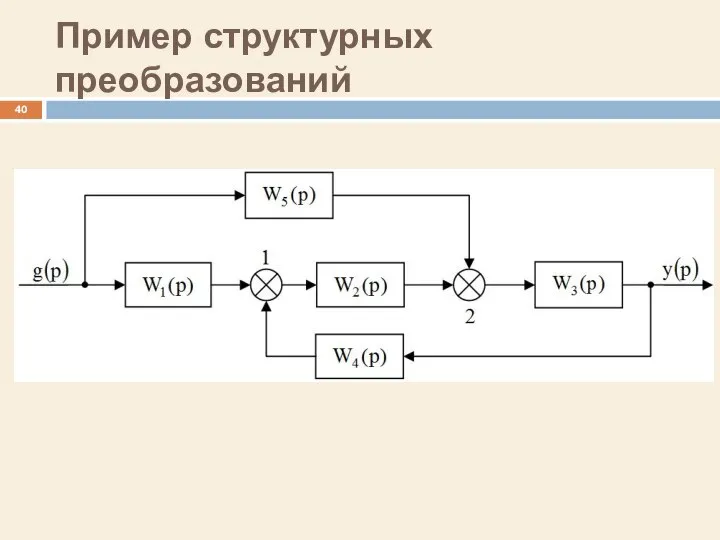
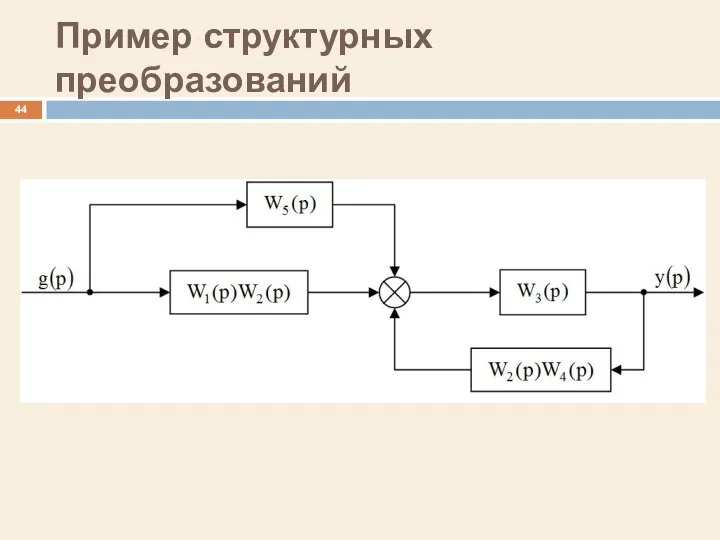
- 40. Пример структурных преобразований
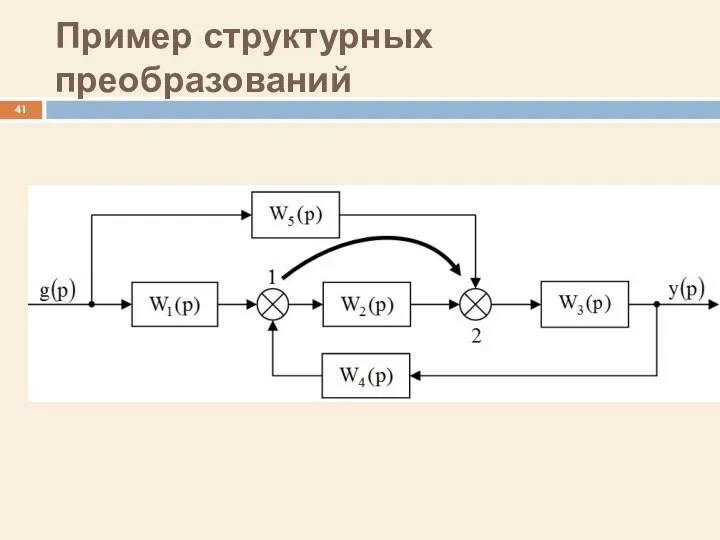
- 41. Пример структурных преобразований
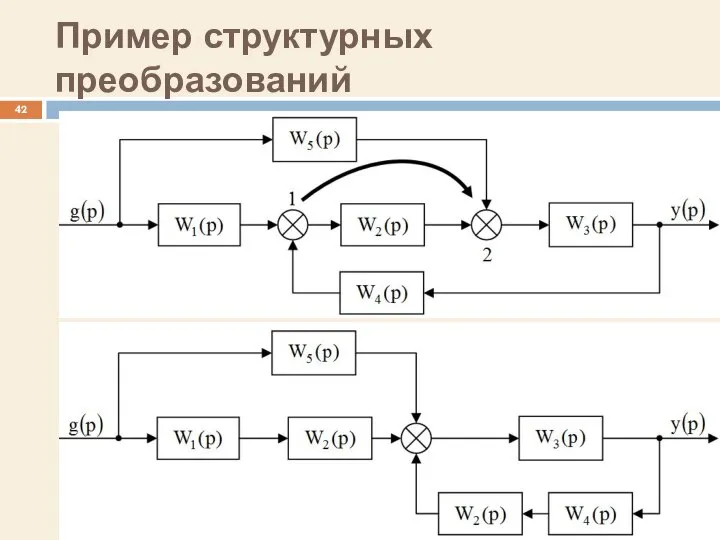
- 42. Пример структурных преобразований
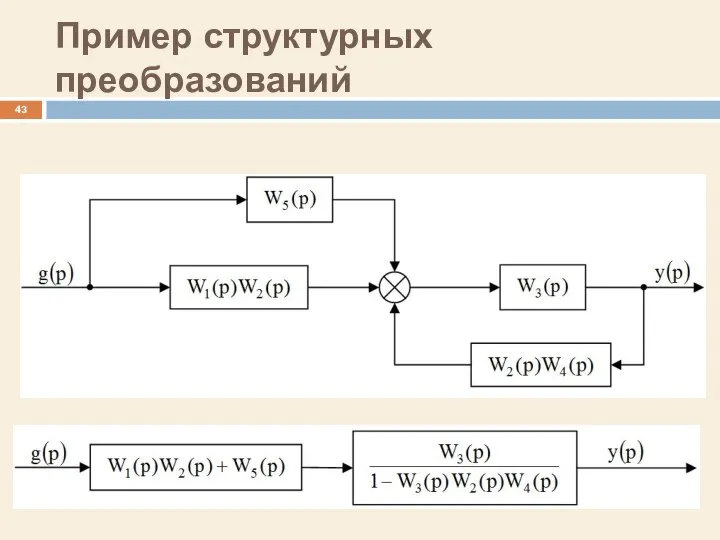
- 43. Пример структурных преобразований
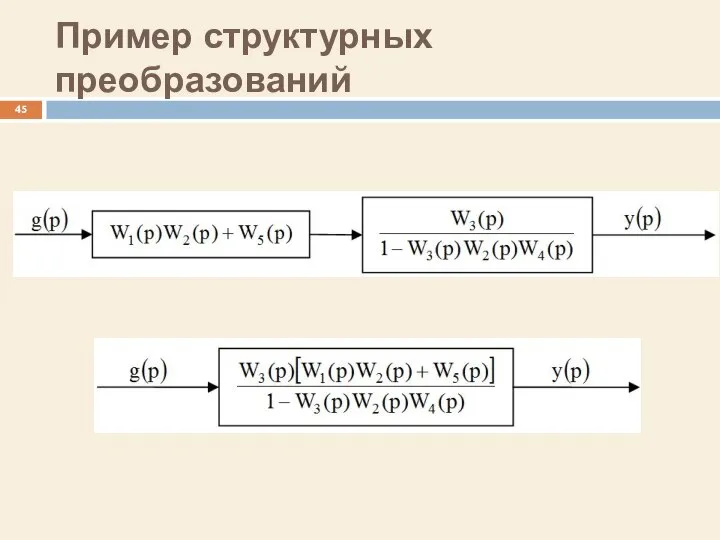
- 44. Пример структурных преобразований
- 45. Пример структурных преобразований
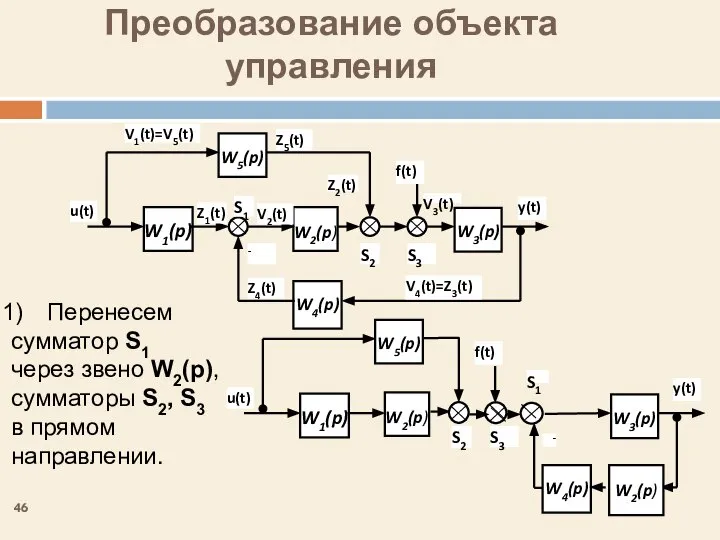
- 46. Преобразование объекта управления Перенесем сумматор S1 через звено W2(p), сумматоры S2, S3 в прямом направлении. S1
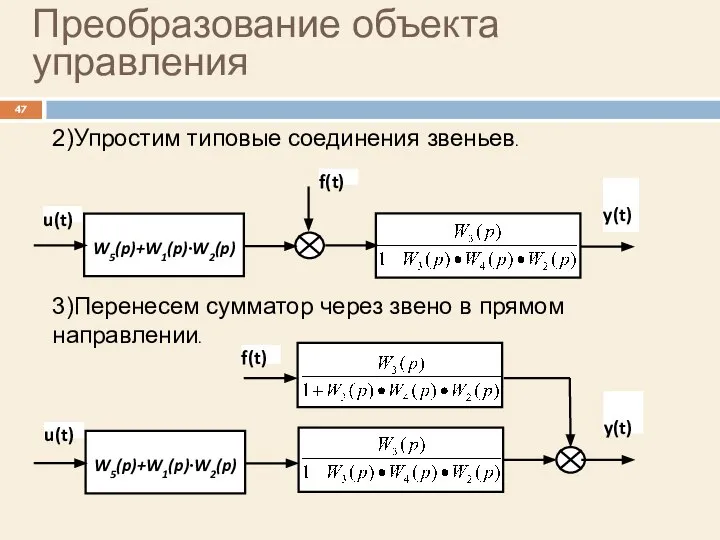
- 47. Преобразование объекта управления 3)Перенесем сумматор через звено в прямом направлении. W5(p)+W1(p)∙W2(p) u(t) y(t) 2)Упростим типовые соединения
- 49. Скачать презентацию














 Солнечная система
Солнечная система Германия. Школы будущего
Германия. Школы будущего My hobby hand made
My hobby hand made Презентация 4
Презентация 4 Духовная культура. Тест
Духовная культура. Тест «Плохие новости из белковой упаковки» Питер Медавар
«Плохие новости из белковой упаковки» Питер Медавар Умножение и деление ( закрепление)
Умножение и деление ( закрепление) Фотоотчёт по производственной практике
Фотоотчёт по производственной практике Человек в экономических отношениях 7 класс
Человек в экономических отношениях 7 класс Стандарт мерчандайзинга Места реализации «ЭЛЬБОР»
Стандарт мерчандайзинга Места реализации «ЭЛЬБОР» Животные тундры
Животные тундры Научно-практическая конференция «Теория развития: дифференционно-интеграционная парадигма» Москва, МГППУ, 24-25 февраля 2009 г. ОНТО
Научно-практическая конференция «Теория развития: дифференционно-интеграционная парадигма» Москва, МГППУ, 24-25 февраля 2009 г. ОНТО Измерение информационного объема сообщения
Измерение информационного объема сообщения Сальвадор Дали
Сальвадор Дали Парные согласные Б и П,звуки [б], [б’], [п], [п’].Строчная буква б.
Парные согласные Б и П,звуки [б], [б’], [п], [п’].Строчная буква б. День туриста (фотографии)
День туриста (фотографии) Золотая пропорция в архитектуре г.Лангепас
Золотая пропорция в архитектуре г.Лангепас Когда любовь в дефиците
Когда любовь в дефиците Биотические связи в природе
Биотические связи в природе Экономическое мышление
Экономическое мышление Презентация на тему Предложения с обращениями и вводными словами (8 класс)
Презентация на тему Предложения с обращениями и вводными словами (8 класс) Правописание гласных и согласных в корнях слов
Правописание гласных и согласных в корнях слов Управление человеческими ресурсами
Управление человеческими ресурсами Триединая цель урока
Триединая цель урока Петровские реформы и понятие моды
Петровские реформы и понятие моды Совушки
Совушки Первая медицинская помощь при травмах опорно-двигательного аппарата
Первая медицинская помощь при травмах опорно-двигательного аппарата Песня про царя Ивана Васильевича, молодого опричника и удалого купца Калашникова
Песня про царя Ивана Васильевича, молодого опричника и удалого купца Калашникова