Тригонометрия

ЕСЛИ
МАТЕМАТИКУ ПОНИМАЕШЬ
– ТО ДЕЛАТЬ НЕЧЕГО,
ЕСЛИ НЕ ПОНИМАЕШЬ, ТО
ТОЖЕ ДЕЛАТЬ НЕЧЕГО.
ВЫБИРАЕМ:
КАКОЕ ДЕЛАТЬ НЕЧЕГО
НАМ БОЛЬШЕ НРАВИТСЯ.
Тригонометрия

Давайте ответим на вопросы:
Почему в среднем звене школы некоторые учащиеся неожиданно начинают хуже успевать?
Почему у некоторых старательных детей пропадает неожиданно интерес к учебе?
Почему в седьмом классе происходит у одних учащихся улучшение в учебе, а у других наоборот ухудшение?
Тригонометрия

Мои выводы:
Учиться надо уметь.
Учить надо так,
чтобы при минимальных затратах
получать максимальную отдачу.
Для этого можно использовать
ассоциативную память.
Тригонометрия

МАТЕМАТИКА –
ЭТО ХОРОШАЯ ИГРУШКА.
ТОЛЬКО НАДО ЗНАТЬ,
КАК В НЕЁ ИГРАТЬ.
Тригонометрия

Тригонометрия
ПОИГРАЕМ
В ТРИГОНОМЕТРИЮ
или
как облегчить себе
и ученикам жизнь

Тригонометрия
С
В
А
а
c
b
Дан прямоугольный треугольник АВС:
Угол С = 900,
сторона, противолежащая углу С
обозначается с,
сторона, противолежащая углу А
обозначается а,
сторона, противолежащая углу В
обозначается b.

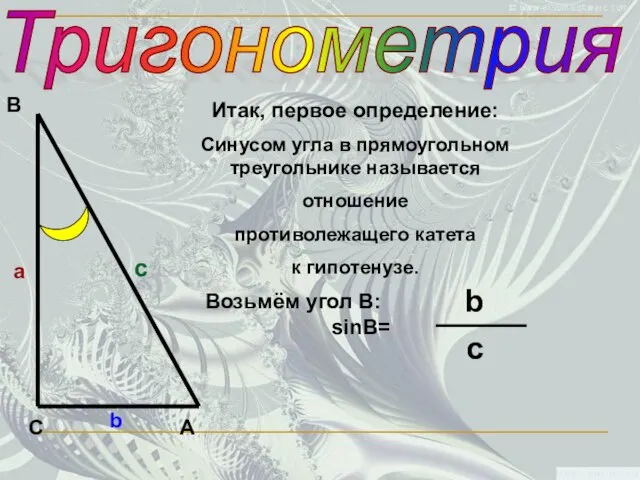
Тригонометрия
С
В
А
а
c
b
Итак, первое определение:
Синусом угла в прямоугольном треугольнике называется
отношение
противолежащего катета
к гипотенузе.
Возьмём угол В:
sinB=
b
c

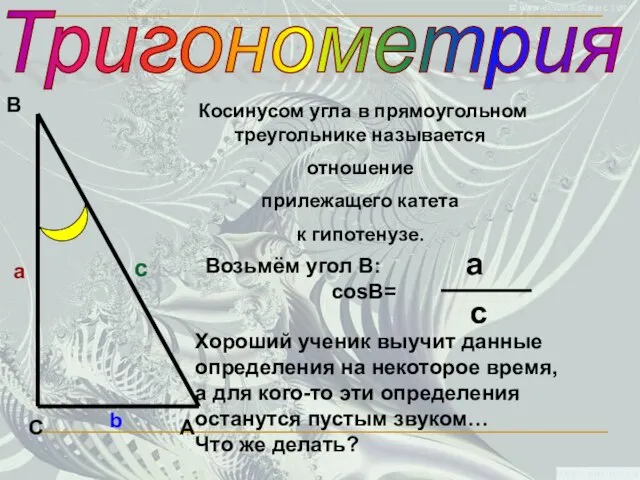
Тригонометрия
С
В
А
а
c
b
Косинусом угла в прямоугольном треугольнике называется
отношение
прилежащего катета
к гипотенузе.
Возьмём угол В:
cosВ=
a
c
Хороший ученик выучит данные определения на некоторое время, а для кого-то эти определения останутся пустым звуком… Что же делать?

Тригонометрия
С
В
А
а
c
b
Играем: Синус ассоциируем со словом
СМОТРИТ
Синус. Что делает?
Смотрит. Куда?
На противолежащий катет.
Относится к чему?
К самой большой стороне – к гипотенузе.
Возьмём угол А:
sinA=
a
c
Играем!

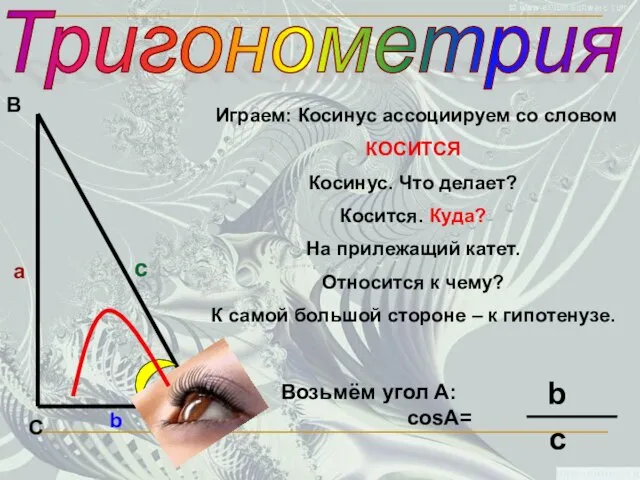
Тригонометрия
С
В
А
а
c
b
Играем: Косинус ассоциируем со словом
КОСИТСЯ
Косинус. Что делает?
Косится. Куда?
На прилежащий катет.
Относится к чему?
К самой большой стороне – к гипотенузе.
Возьмём угол А:
cosA=
b
c

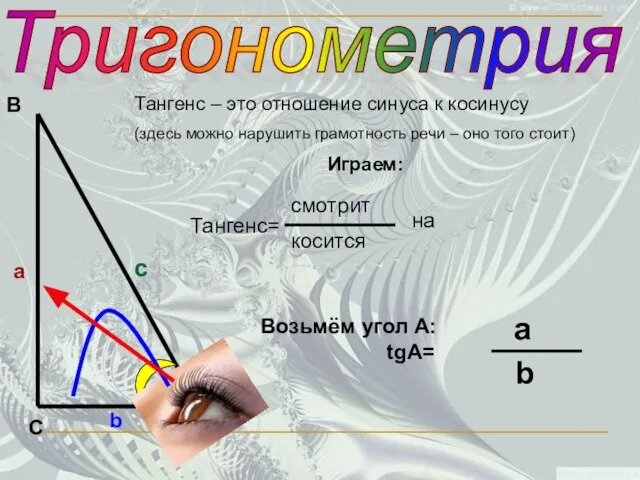
Тригонометрия
С
В
А
а
c
b
Играем:
Возьмём угол А:
tgA=
a
b
Тангенс – это отношение синуса к косинусу
(здесь можно нарушить грамотность речи – оно того стоит)
Тангенс=
смотрит
косится
на

Тригонометрия
Как легко запомнить таблицу значений тригонометрических отношений основных углов в прямоугольном треугольнике?
Для этого надо знать школьный анекдот про Незнайку.
Итак, Незнайке задали во втором классе заполнить ответы к таблице умножения на 9.

Тригонометрия
1 x 9 =
2 x 9 =
3 x 9 =
4 x 9 =
5 x 9 =
6 x 9 =
7 x 9 =
8 x 9 =
9 x 9 =
10 x 9 =
Посмотрел Незнайка на таблицу и сказал:
- Я знаю два ответа: первый и последний…

Тригонометрия
1 x 9 = 9
2 x 9 =
3 x 9 =
4 x 9 =
5 x 9 =
6 x 9 =
7 x 9 =
8 x 9 =
9 x 9 =
10 x 9 = 90
1 x 9 = 9
2 x 9 = 1
3 x 9 = 2
4 x 9 = 3
5 x 9 = 4
6 x 9 = 5
7 x 9 = 6
8 x 9 = 7
9 x 9 = 8
10 x 9 = 90
Вписал Незнайка свои ответы и решил посчитать сколько же примеров он не знал.
И посчитал…

Тригонометрия
1 x 9 = 9
2 x 9 = 18
3 x 9 = 27
4 x 9 = 36
5 x 9 = 45
6 x 9 = 54
7 x 9 = 63
8 x 9 = 72
9 x 9 = 81
10 x 9 = 90
Что-то много я не знаю, - подумал Незнайка и решил пересчитать в обратном порядке
1 x 9 = 9
2 x 9 = 1
3 x 9 = 2
4 x 9 = 3
5 x 9 = 4
6 x 9 = 5
7 x 9 = 6
8 x 9 = 7
9 x 9 = 8
10 x 9 = 90
Этот принцип лежит в основе запоминания значений тригонометрических отношений в прямоугольном треугольнике для основных углов

Тригонометрия
В восьмом классе Незнайка заполнил «–» (минусами)
всё, что он не знал

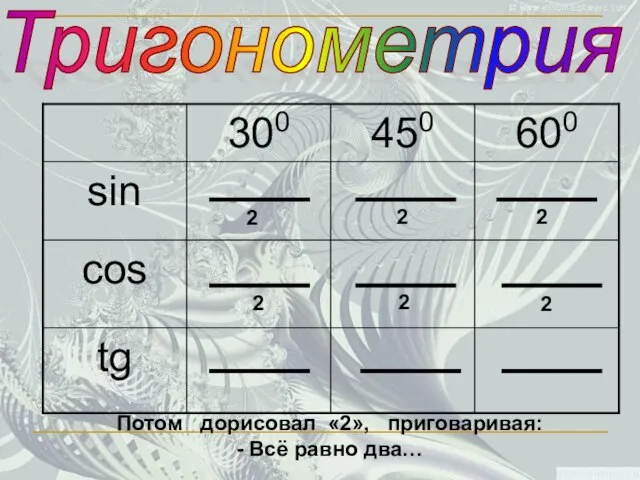
Тригонометрия
2
2
2
2
2
2
Потом дорисовал «2», приговаривая: - Всё равно два…

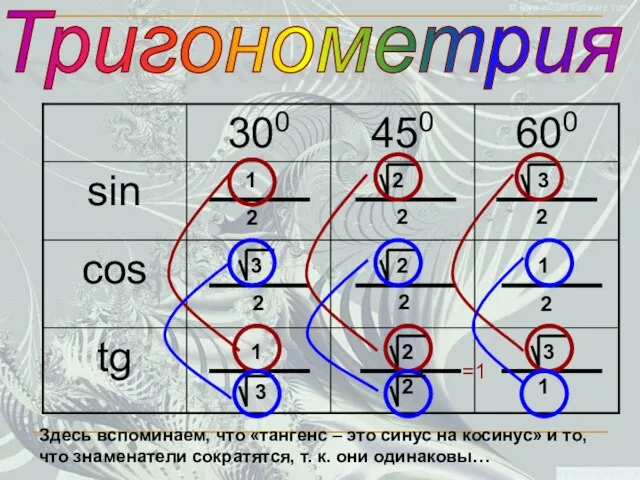
Тригонометрия
2
2
2
2
2
2
2
1
1
2
3
3
Потом посчитал в первой строке в одну сторону, а во второй – в другую сторону, что он не знает…

Тригонометрия
2
2
2
2
2
2
2
1
1
2
3
3
Затем пририсовал значок, который где-то видел…

Тригонометрия
2
2
2
2
2
2
2
1
1
2
3
3
2
3
3
1
1
2
Здесь вспоминаем, что «тангенс – это синус на косинус» и то, что знаменатели сократятся, т. к. они одинаковы…
=1

Тригонометрия
Таблица готова. А как насчёт единичной окружности в тригонометрии? Это же спасательный круг!
Спасайся, кто может!

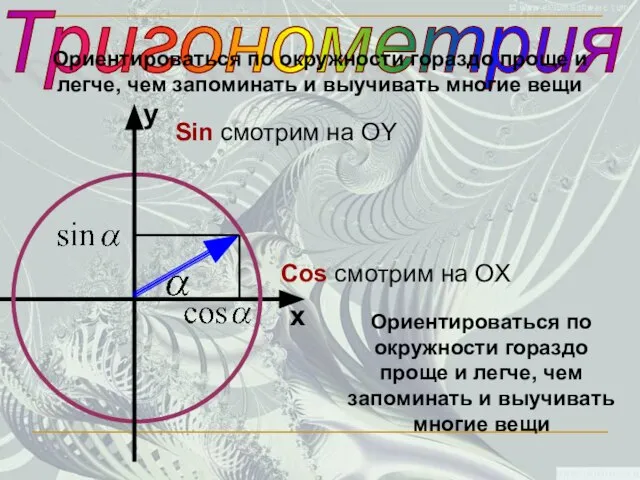
Тригонометрия
Ориентироваться по окружности гораздо проще и легче, чем запоминать и выучивать многие вещи
Sin смотрим на OY
Cos смотрим на OX
Ориентироваться по окружности гораздо проще и легче, чем запоминать и выучивать многие вещи

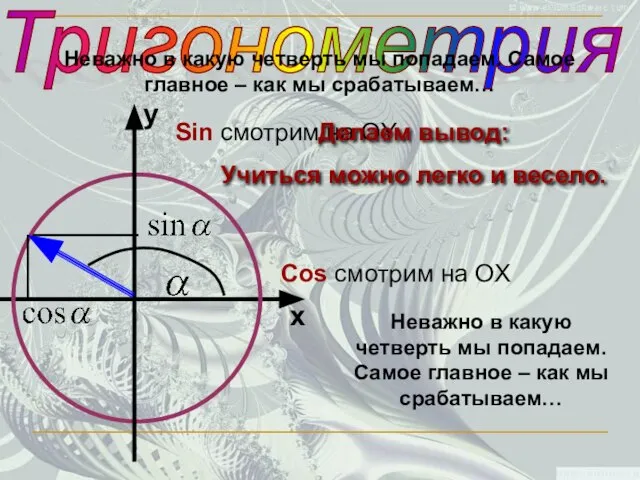
Тригонометрия
Неважно в какую четверть мы попадаем. Самое главное – как мы срабатываем…
Sin смотрим на OY
Cos смотрим на OX
Неважно в какую четверть мы попадаем. Самое главное – как мы срабатываем…
Делаем вывод:
Учиться можно легко и весело.

Тригонометрия
Рассказ учителя, т.е. живое общение, мел и тряпка – незаменимые объекты обучения. И все технические средства не могут передать всех творческих аспектов общения и обучения.
Презентация подготовлена к докладу: «Ассоциативные методы развития памяти на примере изучения темы «Тригонометрия»»
Учитель МОУ СОШ №31 г. Иркутска
Максимова Татьяна Вячеславовна
2009 год