Умножение натуральных чисел и его свойства

Цель
Повторить компоненты произведения чисел.
Изучить понятие произведения натуральных чисел.
Изучить переместительное и сочетательное свойства умножения..

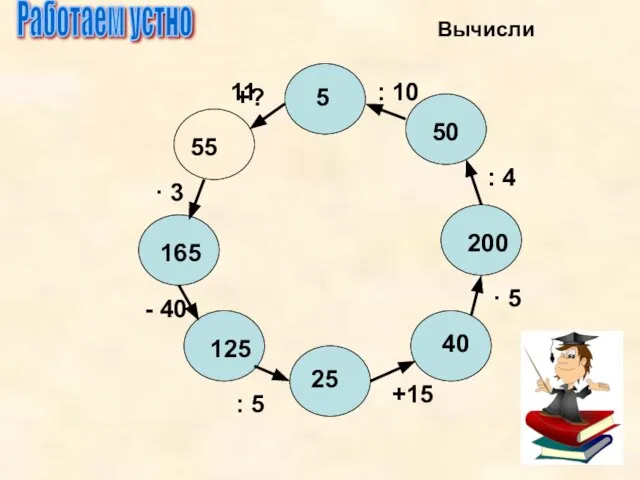
Работаем устно
: 5
25
125
40
200
50
5
55
165
+15
· 5
: 4
: 10
+?
· 3
- 40
11
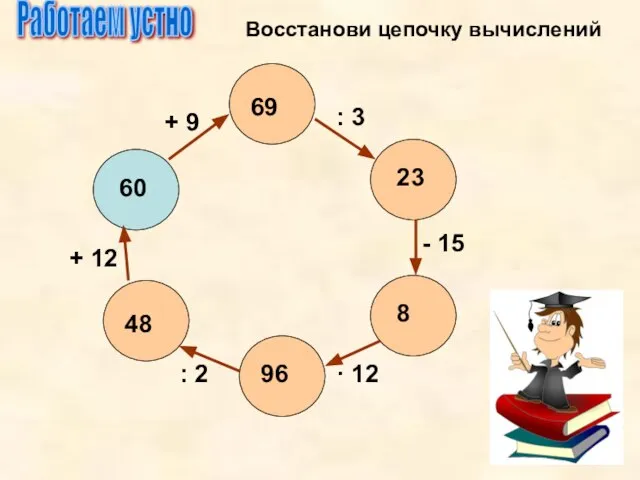
Вычисли

Работаем устно
Восстанови цепочку вычислений
60
69
23
8
96
48
+ 9
: 3
- 15
· 12
: 2
+ 12

Умножение натуральных чисел
и его свойства

Решим задачу
Концертный зал освещается тремя люстрами по 25 лампочек в каждой. Сколько всего лампочек освещают концертный зал?
Решение:
25 + 25 + 25
= 75
Сумму, в которой все слагаемые равны друг другу записывают короче:
25 · 3 = 75

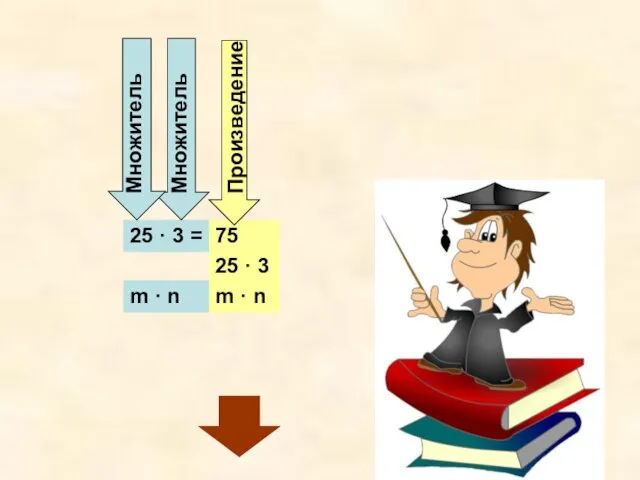
25 · 3 =
25 · 3
75
m · n
m · n
Множитель
Множитель
Произведение

Умножить число m на натуральное число n – значит найти сумму n слагаемых, каждое из которых равно m.
Выражение m · n и значение этого выражения называют произведением чисел m и n. Числа m и n называют множителями.

Представьте в виде произведения
236 + 236 + 236 + 236 =
236 · 4
у + у + у + у + у + у + у =
у · 7
(х+5) + (х+5) + (х+5) =
(х+5) · 3

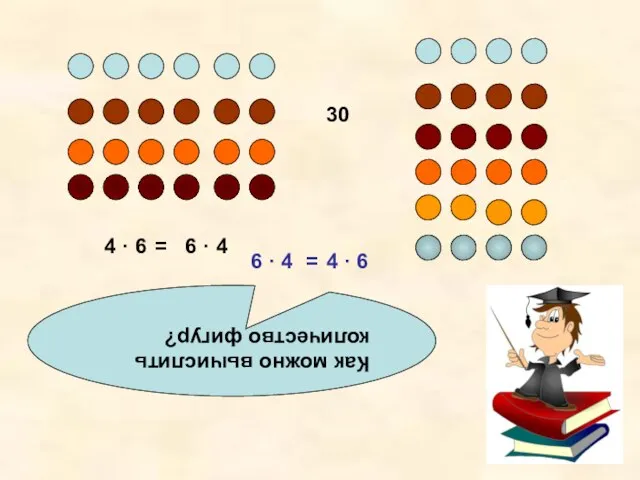
Как можно вычислить количество фигур?
4 · 6
6 · 4
=
4 · 6
6 · 4
=
30

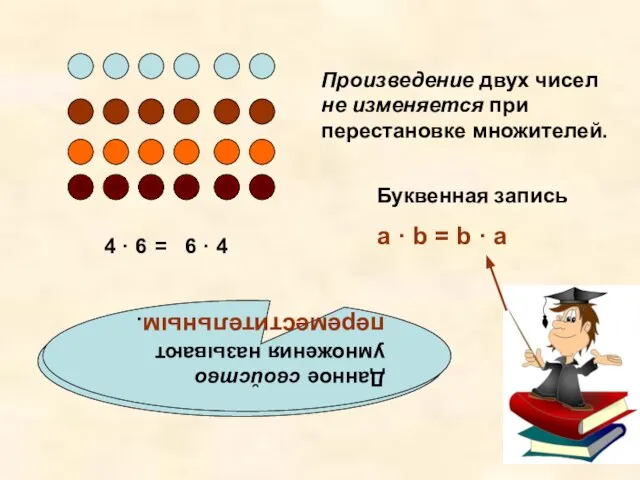
Какой можно сделать вывод?
4 · 6
6 · 4
=
Произведение двух чисел не изменяется при перестановке множителей.
Данное свойство умножения называют переместительным.
Буквенная запись
a · b = b · a

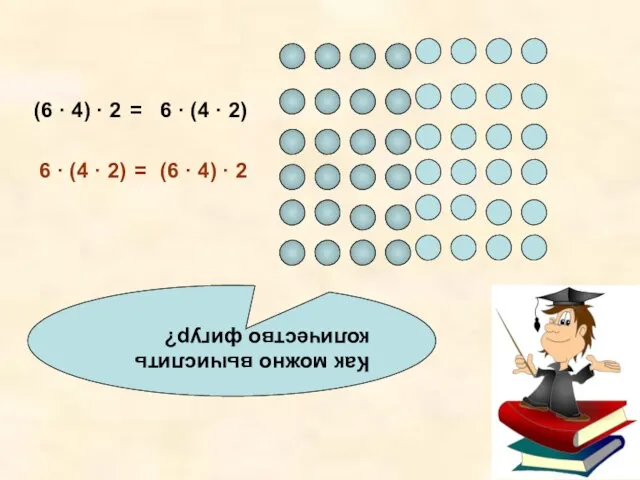
Как можно вычислить количество фигур?
(6 · 4) · 2
6 · (4 · 2)
=
(6 · 4) · 2
6 · (4 · 2)
=

Данное свойство умножения называют сочетательным
(6 · 4) · 2
6 · (4 · 2)
=
(6 · 4) · 2
6 · (4 · 2)
=
Буквенная запись
a · (b · с) = (a · b) · с
Чтобы умножить число на произведение двух чисел, можно его умножить сначала на первый множитель, а потом полученное произведение умножить на второй множитель.

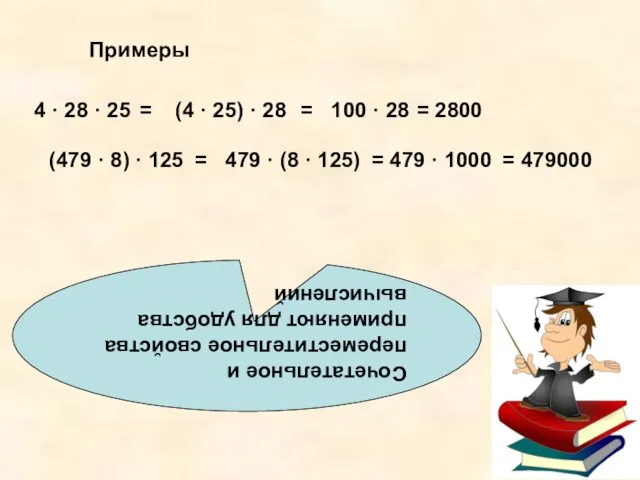
Сочетательное и переместительное свойства применяют для удобства вычислений
Примеры
4 · 28 · 25
=
(4 · 25) · 28
=
100 · 28
= 2800
(479 · 8) · 125
=
479 · (8 · 125)
= 479 · 1000
= 479000

Напомним еще некоторые свойства умножения, известные из начальной школы
Сумма n слагаемых, каждое из которых равно 1, равна n.
Сумма n слагаемых, каждое из которых равно 0, равна 0.
1 · n = n
0 · n = 0

Запомните!
Перед буквенными множителями обычно не пишут знак умножения: вместо 5 · х пишут 5х, вместо a · b пишут ab .
Опускают знак умножения и перед скобками. Например вместо 3 · (х + у) пишут 3(х + у), а вместо (х + 5) · (х – 9) пишут (х + 5)(х – 9)

Решите из учебника
№ 404, 405, 406, 412 (а – е), 414

Задание на дом
п. 11, № 450, 451, 452