Содержание
- 2. Методы решения тригонометрических уравнений. УРОК – ЭКСКУРСИЯ в научно- исследовательский институт sin x = 1 2sin2x
- 4. Получи пропуск. Каково будет решение уравнения cos x = a при а > 1
- 5. Проверочная работа. 5. В каком промежутке находится arccos a ? 5. В каком промежутке находится arcsin
- 6. Проверочная работа. 9. Каким будет решение уравнения cos x = 0? 9. Каким будет решение уравнения
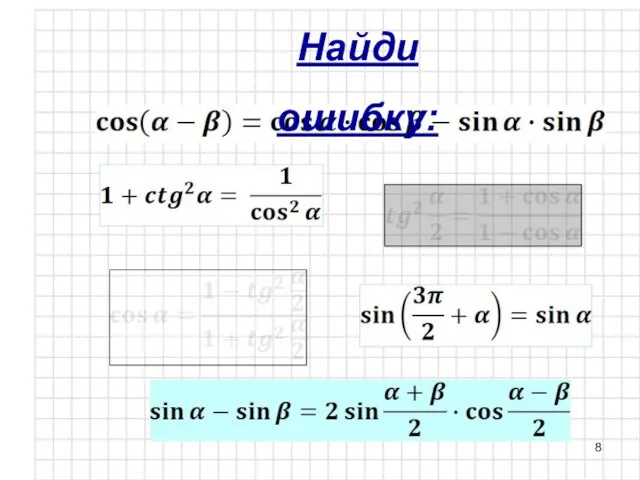
- 8. Найди ошибку:
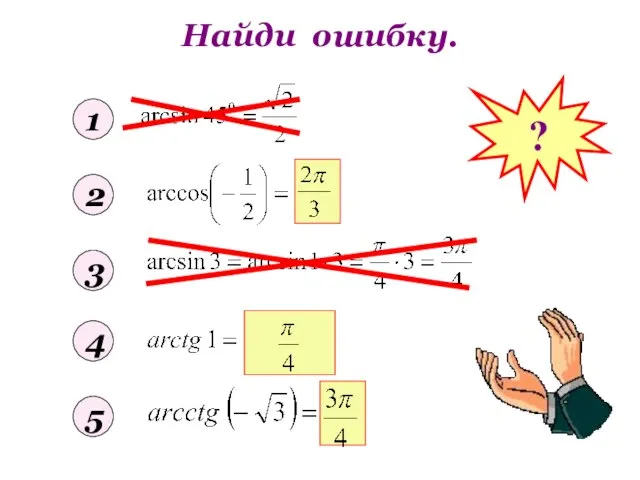
- 9. Найди ошибку. 1 2 3 4 5 ?
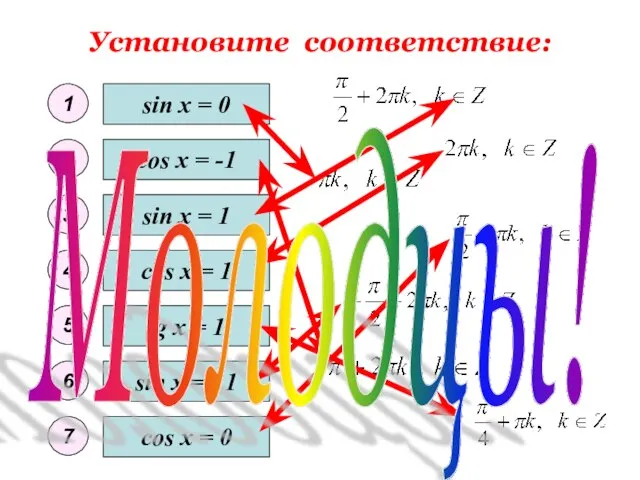
- 10. Установите соответствие: sin x = 0 sin x = - 1 sin x = 1 cos
- 11. Установите соответствие: sin x = 0 sin x = - 1 sin x = 1 cos
- 12. Аукцион идей «Классификация уравнений» 1.
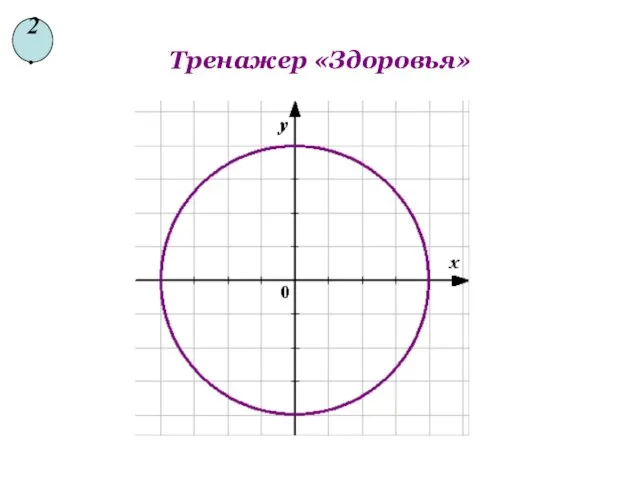
- 13. Тренажер «Здоровья» 2.
- 14. Проект «Методы решения уравнения sin x + cos x = 1 » 3. «Решай, твори, ищи
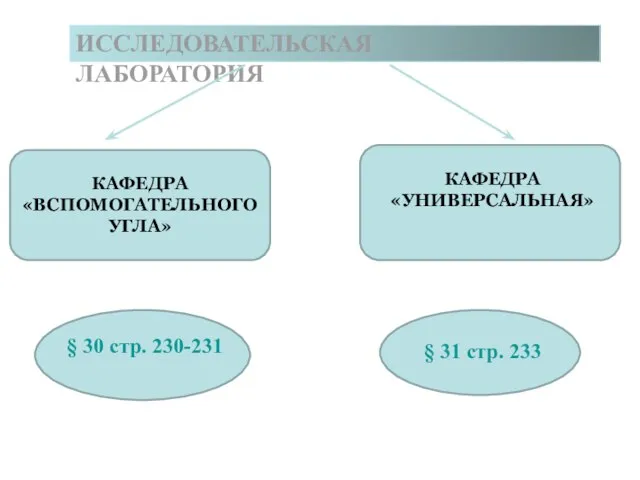
- 15. ИССЛЕДОВАТЕЛЬСКАЯ ЛАБОРАТОРИЯ КАФЕДРА «ВСПОМОГАТЕЛЬНОГО УГЛА» КАФЕДРА «УНИВЕРСАЛЬНАЯ» § 30 стр. 230-231 § 31 стр. 233
- 16. Игра «Верите ли вы, что …» 1. … cos π = -1 2. … sin (π/4)
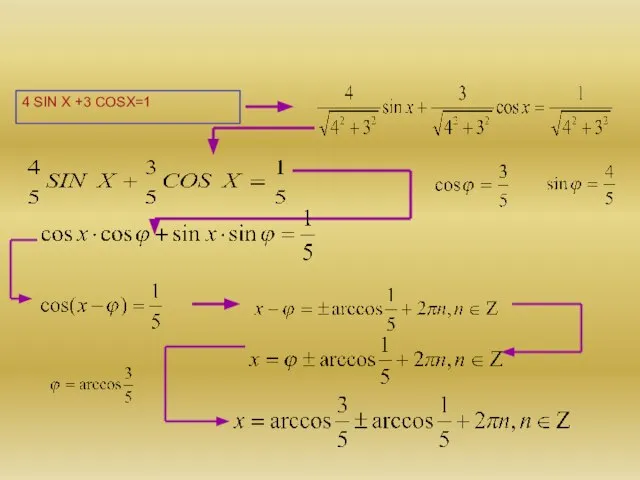
- 17. МЕТОД ВСПОМОГАТЕЛЬНОГО АРГУМЕНТА
- 18. ПРИМЕР 4 SIN X +3 COSX=1
- 19. Восстановить правую часть: 1/2 1 2 1/2
- 20. Выставочный зал Франсуа Виет, французский математик. По профессии – юрист. В 1591 году ввел буквенные обозначения
- 21. Выставочный зал Современный вид тригонометрия получила в трудах Леонарда Эйлера. Впервые в его работах встречаются символы
- 22. Выставочный зал В XV веке немецкий астроном И.Мюллер издал работу «Пять книг о треугольниках всех видов».
- 23. Выставочный зал Ученый из Беларуси Иван Петрович Дóлбня высказал идею определять тригонометрические функции синус и косинус
- 24. Домашнее задание: Составить проект решения любого уравнения Решить уравнение: Спасибо за урок!
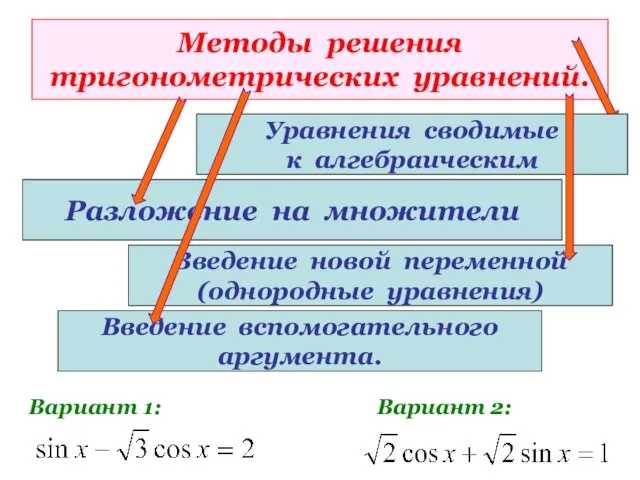
- 25. Методы решения тригонометрических уравнений. Уравнения сводимые к алгебраическим. Вариант 1: Вариант 2: Необходимо выбрать соответствующий прием
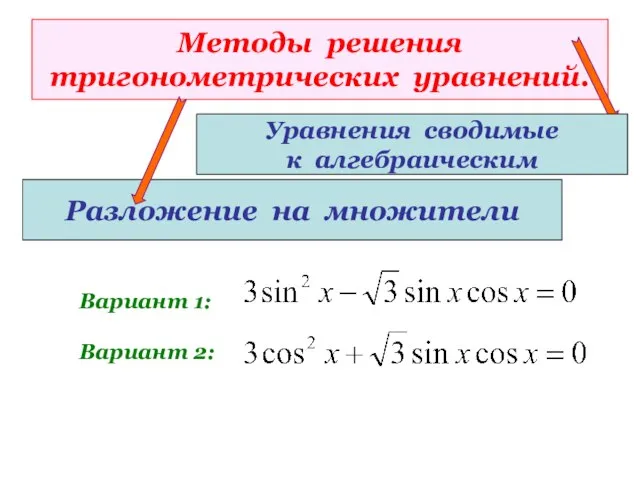
- 26. Методы решения тригонометрических уравнений. Разложение на множители Вариант 1: Вариант 2: Уравнения сводимые к алгебраическим
- 27. Методы решения тригонометрических уравнений. Разложение на множители Вариант 1: Вариант 2: Уравнения сводимые к алгебраическим Введение
- 28. Методы решения тригонометрических уравнений. Разложение на множители Вариант 1: Вариант 2: Уравнения сводимые к алгебраическим Введение
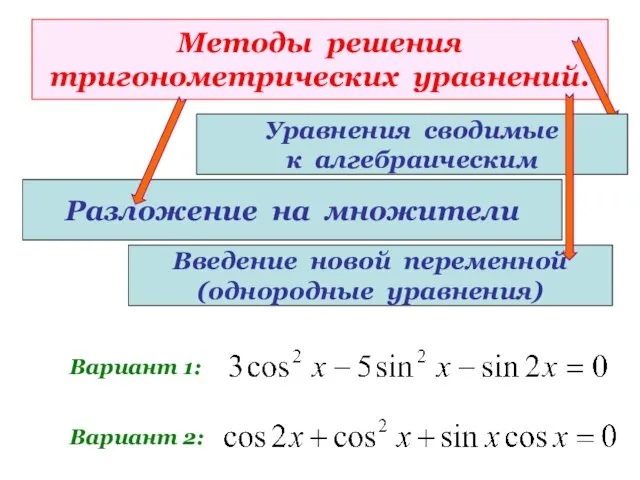
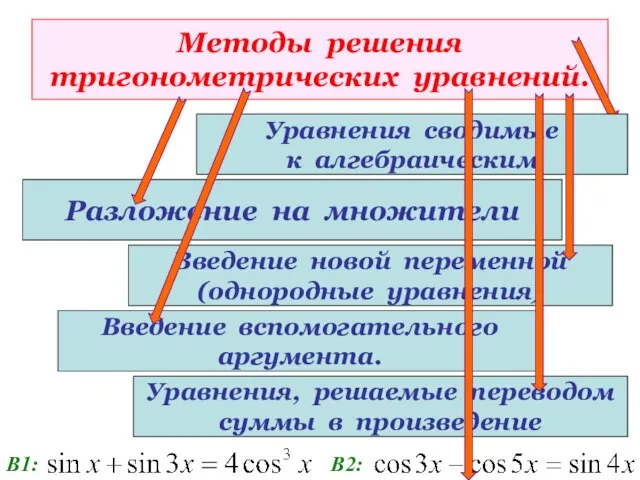
- 29. Методы решения тригонометрических уравнений. Разложение на множители Уравнения сводимые к алгебраическим Введение новой переменной (однородные уравнения)
- 31. Скачать презентацию


















 Управление социальными рисками и кризисами
Управление социальными рисками и кризисами  Компас – это прибор, который помогает определить стороны света. Красная стрелка всегда показывает на юг, а синяя на север. Справа б
Компас – это прибор, который помогает определить стороны света. Красная стрелка всегда показывает на юг, а синяя на север. Справа б Поликультурный мир Республики Марий Эл: проблемы диаспор и землячеств
Поликультурный мир Республики Марий Эл: проблемы диаспор и землячеств Русский народный костюм
Русский народный костюм Монотипия
Монотипия Презентация на тему Весна Весенние приметы
Презентация на тему Весна Весенние приметы Междисциплинарная олимпиада по физике, математике и информатике
Междисциплинарная олимпиада по физике, математике и информатике Тема: «Проектная деятельность в коррекционной работе детского сада»
Тема: «Проектная деятельность в коррекционной работе детского сада» Добрый вечер, уважаемые родители!Поздравляем с началом учебного годаЖелаем терпения, сотрудничества, хороших успехов в учении
Добрый вечер, уважаемые родители!Поздравляем с началом учебного годаЖелаем терпения, сотрудничества, хороших успехов в учении Тайм менеджмент
Тайм менеджмент  Культура Тибета
Культура Тибета Технология возведения подземных инженерных сооружений
Технология возведения подземных инженерных сооружений Видатки на військову та цивільну оборону
Видатки на військову та цивільну оборону Южная ссылка 1820 - 1824
Южная ссылка 1820 - 1824 Алексей Назарович
Алексей Назарович Ұлттық таба нан өніміне ақпараттық шолу жасау; таба нанның сапа көрсеткіштерін анықтау
Ұлттық таба нан өніміне ақпараттық шолу жасау; таба нанның сапа көрсеткіштерін анықтау Презентация на тему Повесть Гоголя «Тарас Бульба»
Презентация на тему Повесть Гоголя «Тарас Бульба»  5._Как_стать_личностью
5._Как_стать_личностью Данься. Визитная карточка объекта всемирного наследия ЮНЕСКО
Данься. Визитная карточка объекта всемирного наследия ЮНЕСКО Слова із прямим і переносним значенням
Слова із прямим і переносним значенням Проблематика литературы
Проблематика литературы Приготовление воскресного завтрака для всей семьи
Приготовление воскресного завтрака для всей семьи Презентация на тему Реки и озёра Южной Америки
Презентация на тему Реки и озёра Южной Америки Освещение жилого дома
Освещение жилого дома Разберёмся с «Атмосферным давлением»
Разберёмся с «Атмосферным давлением» Презентация на тему Ахатина иммакулята пантера
Презентация на тему Ахатина иммакулята пантера  Экология и Экономика
Экология и Экономика Психическое развитие детей с нарушениями речи
Психическое развитие детей с нарушениями речи