ВЕРИФИКАЦИЯ ПРОГРАММЫ COSMOS/M ДЛЯ РАСЧЕТА НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ЭЛЕМЕНТОВ И УЗЛОВ ОБОРУДОВАНИЯ И ТРУБОПРОВОДОВ АЭУ

1. Определение напряженного состояния цилиндрической оболочки с эллиптическим днищем под действием равномерно распределенного давления (см. рис.1).
Входные данные.
E = 200000 МПа – модуль упругости;
ν = 0.3 – коэффициент Пуассона;
r = 0.5 м – радиус цилиндра по средней линии;
H = 0.5*r = 0.25 м – высота эллиптического днища;
t = 0.005 м – толщина обечайки и днища;
P = 1 МПа – внутреннее давление.
Конечно – элементная модель. В данной задаче использовались три конечно – элементных модели. Для конечных элементов типа PLANE2D и SHELL3 использовалась сетка из 900 элементов. Для комбинации конечных элементов типа SHELL3 и SHELL4 использовалась сетка из 856 элементов.
Подобласть верификации. Проверка точности расчета максимальных окружных и меридиональных напряжений в центре эллиптического днища и вблизи зоны перехода обечайка – эллиптическое днище (зона А, рисунок 1).
Рис. 1

Аналитическое решение. Формулы для определения максимальных напряжений имеют следующий вид [4]:
зона А - окружные напряжения;
- меридиональные напряжения
центр эллиптического днища
Точность решения. Сравнение результатов расчета окружных и меридиональных напряжений, полученных по программе Cosmos/M с использованием элементов типа PLANE2D, SHELL3 и комбинации элементов типа SHELL3 и SHELL4, с аналитическим решением представлены в таблице 1.
Таблица 1
Совпадение результатов, представленных в таблице 1, можно считать удовлетворительным.
В данной таблице η - относительная погрешность, %.

2. Определение экстремальных напряжений в зоне сопряжения шаровой емкости с цилиндрической опорой под действием веса шаровой емкости с жидкостью (см. рис.2).
Рис. 2
Входные данные
E = 200000 МПа – модуль упругости;
ν = 0.3 – коэффициент Пуассона;
r = 4.325 м – радиус цилиндрической опоры;
R = 5.25 м – радиус сферической емкости;
h1 = 0.025 м – толщина стенки сферы;
h2 = 0.02 м – толщина стенки цилиндрической опоры;
G = 6906000 Н – вес емкости с жидкостью.
Конечно – элементная модель. В данной задаче для элементов типа SHELL3 использовались три конечно – элементных модели со средними размерами элементов 339.6 мм , 169.8 мм и 84.49 мм.
Подобласть верификации. Проверка точности расчета экстремальных напряжений в зоне сопряжения шаровой емкости с цилиндрической обечайкой (зона А, рисунок 2) при различных конечно – элементных схемах.
Аналитическое решение. Аналитическое решение данной задачи описано в [4]. В таблице 2 помещены результаты расчета, приведенные в этой же работе.
Точность решения. Сравнение результатов расчета экстремальных напряжений в зоне сопряжения шаровой емкости с цилиндрической обечайкой (зона А, рисунок 2), полученных по программе Cosmos/M с использованием элементов типа SHELL3, с аналитическим решением представлены в таблице 2.

Таблица 2
Экстремальные напряжения в плоскости Z = 0
В данной таблице:
σ - экстремальные напряжения;
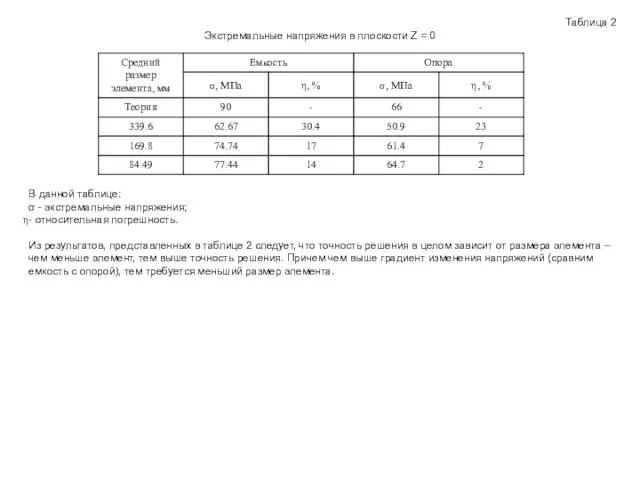
- относительная погрешность.
Из результатов, представленных в таблице 2 следует, что точность решения в целом зависит от размера элемента – чем меньше элемент, тем выше точность решения. Причем чем выше градиент изменения напряжений (сравним емкость с опорой), тем требуется меньший размер элемента.

3. Определение максимальных продольных напряжений в цилиндрической оболочке с жесткой плоской крышкой под действием внутреннего давления (см. рис.3).
Рис. 3
Входные данные
E = 200000 МПа – модуль упругости;
ν = 0.3 – коэффициент Пуассона;
H = 0.03 м – толщина днища;
h = 0.003 м – толщина цилиндрической обечайки;
D = 0.2 м – диаметр цилиндрической обечайки;
P = 1 МПа – внутреннее давление.
Конечно – элементная модель. В данной задаче для элементов типа SHELL3 использовалась конечно – элементная модель, состоящая из 1726 узлов (см. рис. 4).
Рис. 4
Подобласть верификации. Проверка точности расчета максимальных продольных напряжений в цилиндрической оболочке с жесткой плоской крышкой под действием внутреннего давления (один из вариантов краевой задачи).
Аналитическое решение. Аналитическое решение данной задачи описано в [5].
Максимальные продольные напряжения в цилиндрической оболочке возникают в краевой зоне в районе сопряжения оболочки и днища

Точность решения. Сравнение результатов расчета максимальных напряжений, полученных по программе Cosmos/M с использованием элементов типа SHELL3, с аналитическим решением представлены в таблице 3.
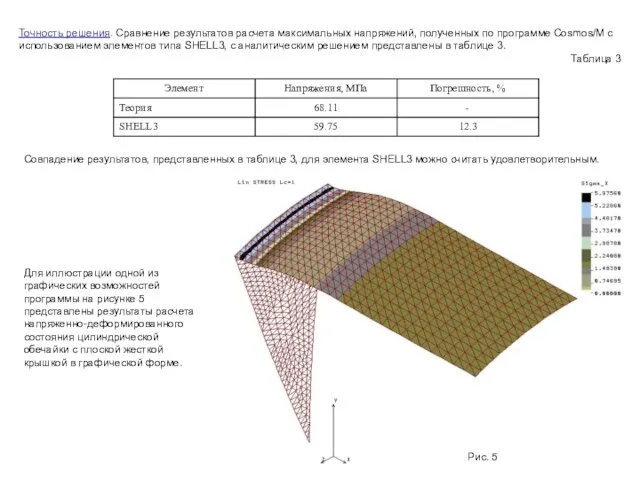
Таблица 3
Совпадение результатов, представленных в таблице 3, для элемента SHELL3 можно считать удовлетворительным.
Для иллюстрации одной из графических возможностей программы на рисунке 5 представлены результаты расчета напряженно-деформированного состояния цилиндрической обечайки с плоской жесткой крышкой в графической форме.
Рис. 5

Входные данные
E = 200000 МПа – модуль упругости для стали;
Eп = 3000 МПа – модуль упругости материала прокладки;
ν = 0.3 – коэффициент Пуассона;
Alfa = 0.115 *10-4 ед/оК – коэффициент линейного расширения для стали;
Fз = 6178.5 Н – усилие начального затяга шпильки;
Рр = 0.12 МПа – рабочее давление;
Рп = 0.15 МПа – давление гидроиспытаний
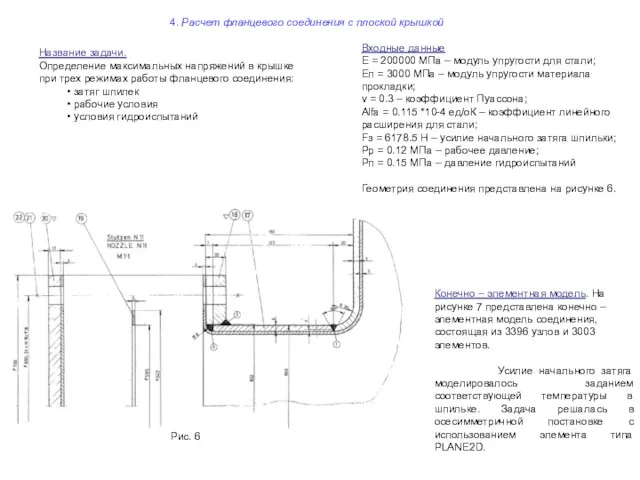
Геометрия соединения представлена на рисунке 6.
4. Расчет фланцевого соединения с плоской крышкой
Название задачи.
Определение максимальных напряжений в крышке при трех режимах работы фланцевого соединения:
затяг шпилек
рабочие условия
условия гидроиспытаний
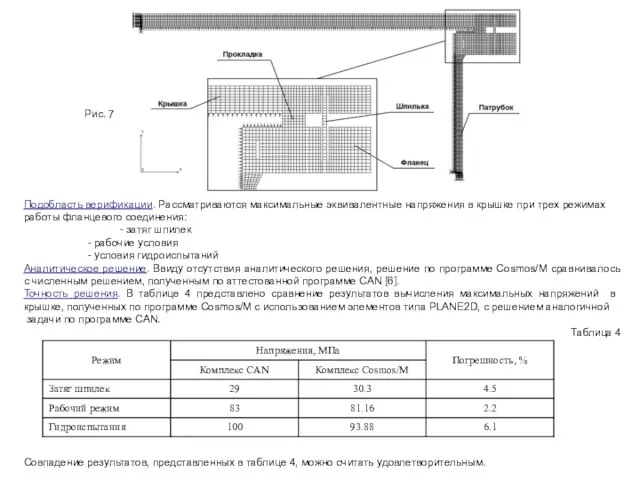
Конечно – элементная модель. На рисунке 7 представлена конечно – элементная модель соединения, состоящая из 3396 узлов и 3003 элементов.
Усилие начального затяга моделировалось заданием соответствующей температуры в шпильке. Задача решалась в осесимметричной постановке с использованием элемента типа PLANE2D.
Рис. 6

Рис. 7
Подобласть верификации. Рассматриваются максимальные эквивалентные напряжения в крышке при трех режимах работы фланцевого соединения:
- затяг шпилек
- рабочие условия
- условия гидроиспытаний
Аналитическое решение. Ввиду отсутствия аналитического решения, решение по программе Cosmos/M сравнивалось с численным решением, полученным по аттестованной программе CAN [6].
Точность решения. В таблице 4 представлено сравнение результатов вычисления максимальных напряжений в крышке, полученных по программе Cosmos/M с использованием элементов типа PLANE2D, с решением аналогичной
задачи по программе CAN.
Таблица 4
Совпадение результатов, представленных в таблице 4, можно считать удовлетворительным.

5. Определение напряжений в составном, соединенном с натягом цилиндре.
Рис. 8

Подобласть верификации. Рассматриваются контактное давление и окружные напряжения на внутренней и наружной поверхностях составного цилиндра.
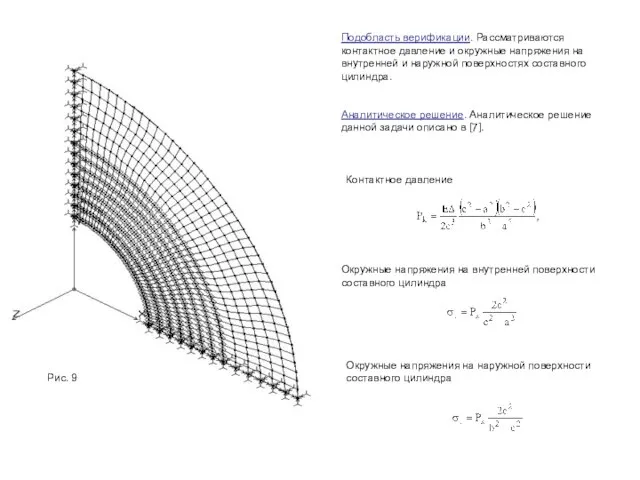
Аналитическое решение. Аналитическое решение данной задачи описано в [7].
Контактное давление
Окружные напряжения на внутренней поверхности составного цилиндра
Окружные напряжения на наружной поверхности составного цилиндра

Точность решения. В таблице 5 представлено сравнение результатов вычисления контактного давления и окружных напряжений на внутренней и наружной поверхностях составного цилиндра, полученных по программе Cosmos/M с использованием элементов типа PLANE2D.
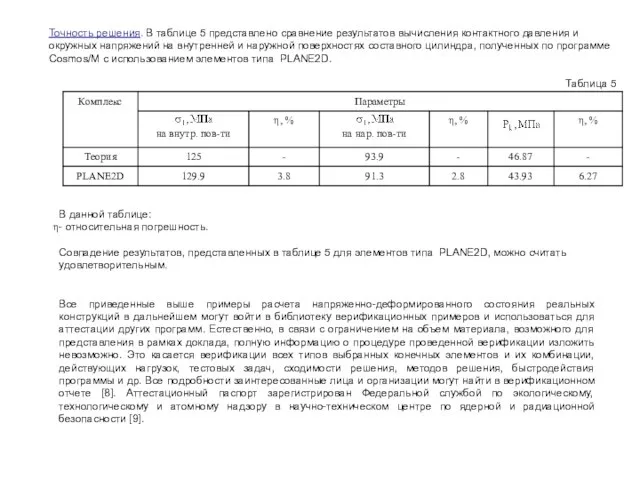
Таблица 5
В данной таблице:
- относительная погрешность.
Совпадение результатов, представленных в таблице 5 для элементов типа PLANE2D, можно считать удовлетворительным.
Все приведенные выше примеры расчета напряженно-деформированного состояния реальных конструкций в дальнейшем могут войти в библиотеку верификационных примеров и использоваться для аттестации других программ. Естественно, в связи с ограничением на объем материала, возможного для представления в рамках доклада, полную информацию о процедуре проведенной верификации изложить невозможно. Это касается верификации всех типов выбранных конечных элементов и их комбинации, действующих нагрузок, тестовых задач, сходимости решения, методов решения, быстродействия программы и др. Все подробности заинтересованные лица и организации могут найти в верификационном отчете [8]. Аттестационный паспорт зарегистрирован Федеральной службой по экологическому, технологическому и атомному надзору в научно-техническом центре по ядерной и радиационной безопасности [9].