ВЫБОРОЧНОЕ ИССЛЕДОВАНИЕ

Выборочное статистическое исследование – это обследование выборочной совокупности с целью получения достоверных суждений о характеристиках или параметрах генеральной совокупности.
Генеральная совокупность – это полная совокупность единиц ( вся статистическая совокупность).
Выборочная совокупность (выборка) - это часть единиц генеральной совокупности, отобранная в случайном порядке.
Обозначения:
объем генеральной совокупности – N;
объем выборки - n

Почему выборочному наблюдению отдается предпочтение перед сплошным?
1) с целью экономии времени и средств в результате сокращения объема работы (при выборочном методе обследованию подвергается 5-10%, реже до 15-20% изучаемой совокупности);
2) чтобы свести к минимуму порчу или уничтожение исследуемых объектов (например, при определении прочности пряжи на разрыв нити, при испытании электрических лампочек на продолжительность горения, при проверке консервов на доброкачественность);
3) вследствие того, что исследуемая совокупность может быть полностью недоступна;
4) вследствие того, что исследуемая совокупность может не иметь конечного объема.

Наиболее часто исследуемые с помощью выборочного метода характеристики совокупности:

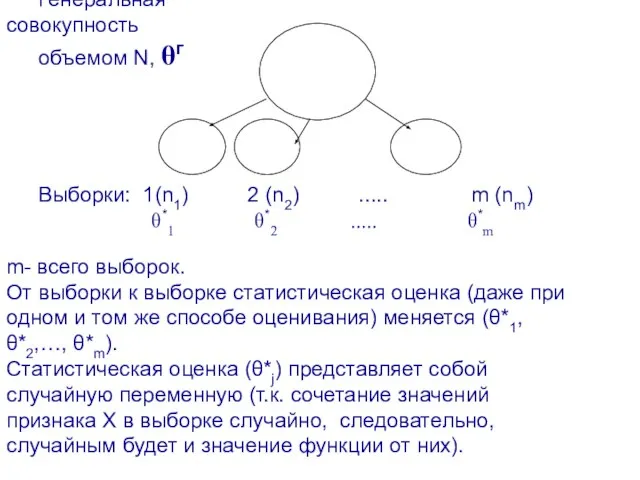
По данным выборки мы не можем найти точное значение характеристики (параметра) генеральной совокупности, а можем только получить его приближенное значение (оценку).
Статистической оценкой (θ*) характеристики (параметра) генеральной совокупности называют приближенное значение этой характеристики (параметра), полученное по некоторой функции от наблюдаемых в выборке значений признака
Х (х1, х2, ...хn), т.е.:
θ*=f(х1, х2, ... ,хn),
где n – объем выборки;
(х1, х2, ..., хn) – рассматриваются как независимые случайные величины.
Функцию (f) называют способом оценивания.

m- всего выборок.
От выборки к выборке статистическая оценка (даже при одном и том же способе оценивания) меняется (θ*1, θ*2,…, θ*m).
Статистическая оценка (θ*j) представляет собой случайную переменную (т.к. сочетание значений признака Х в выборке случайно, следовательно, случайным будет и значение функции от них).
Генеральная совокупность
объемом N, θг
Выборки: 1(n1) 2 (n2) ..... m (nm)
θ*1 θ*2 ..... θ*m

Для одной и той же характеристики (параметра) генеральной совокупности может быть предложено несколько способов оценивания. Возникает проблема выбора лучшего способа оценивания.
Критерием выбора является требование состоятельности, несмещенности и эффективности оценки.
Способ оценивания дает состоятельные оценки, если при бесконечно большом объеме выборки значение статистической оценки стремится к искомому значению характеристики (параметра) генеральной совокупности.

Способ оценивания дает несмещенные оценки, если математическое ожидание оценки при данном способе оценивания тождественно искомой характеристике (параметру) генеральной совокупности (при любом объеме выборки), т.е. М(θ*)=θг. Если математическое ожидание оценки не равняется характеристике генеральной совокупности, то оценка называется смещенной. И разность М(θ*) - θг называется смещением.
Способ оценивания дает эффективные оценки, если дисперсия оценки минимальна (при заданном объеме выборки n) в сравнении с другими способами отбора.

Статистическая оценка, полученная по данным выборки, отличается от генеральной характеристики (параметра) на величину ошибки выборки.
Ошибка выборки состоит из двух частей: ошибки регистрации и ошибки репрезентативности.

Ошибки репрезентативности (представительности) возникают в результате того, что состав отобранной для обследования части единиц совокупности недостаточно полно отображает состав всей изучаемой совокупности (иначе говоря не все типы явления представлены в выборке).
В дальнейшем будем предполагать, что ошибка регистрации равна нулю. Следовательно, ошибка выборки равна ошибке репрезентативности.

Различают среднюю и предельную ошибки выборки.
Средняя ошибка выборки (μ) – это среднее (по выборкам) отклонение выборочной оценки от истинного значения генеральной характеристики.
В каждой конкретной выборке фактическая ошибка выборки может быть меньше средней ошибки, равна ей или больше ее. Причем каждое из этих расхождений имеет различную вероятность.

Предельная ошибка выборки (Δ) – это максимально возможная при данной вероятности ошибка выборки.
То есть мы с заданной вероятностью (Рдов) гарантируем, что оценка ,полученная по нашей конкретной выборке, будет отличаться от значения генеральной характеристики не больше, чем на величину предельной ошибки Δ.

Вероятность, с которой мы гарантируем, что ошибка нашей выборки не превысит предельную ошибку, называется доверительной вероятностью - Рдов.
Предельная ошибка рассчитывается по формуле: Δ=t·μ,
где t- коэффициент доверия, значение которого определяется доверительной вероятностью (Рдов). Чем больше Рдов, тем больше t.

Закон больших чисел – методологическая основа выборочного метода.
Теоретической основой выборочного метода является закон больших чисел:
С увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются (т.е. чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).

Математически данный закон записывается через неравенство П.Л.Чебышева:
где ε - ошибка выборки; n – объем выборки;
- выборочное среднее;
- генеральное среднее.
Следует отметить, что данное неравенство справедливо для генеральной совокупности с ограниченной дисперсией.

Центральная предельная теорема А.М.Ляпунова:
При достаточно большом числе независимых наблюдений вероятность того, что расхождение между выборочной и генеральной средней не превысит по модулю некоторую величину μ·t, равна интегралу Лапласа Ф(t):
(это справедливо для генеральной совокупности с конечной средней и ограниченной дисперсией).

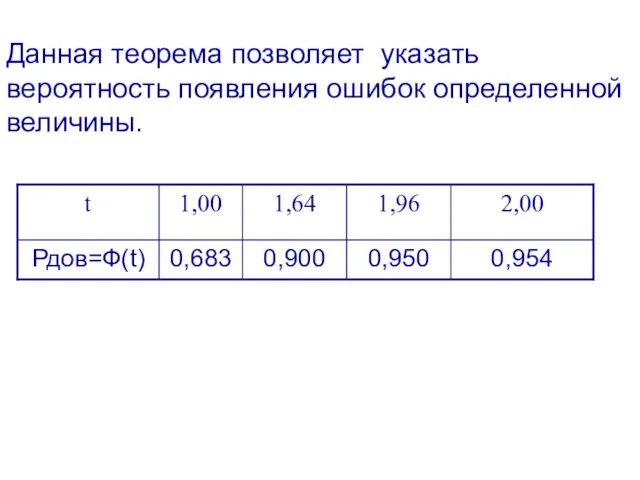
Данная теорема позволяет указать вероятность появления ошибок определенной величины.

Из центральной предельной теоремы следует важный вывод:
при достаточно большом числе независимых наблюдений (объеме выборки) распределение отклонений выборочных средних от генеральной средней (а, следовательно, и самих выборочных средних) приближенно нормально.
При небольшом объеме выборки (n<30)
- интегральная функция распределения Стьюдента.

Классификация способов отбора
1. Повторный и бесповторный отбор
При повторном отборе общая численность единиц генеральной совокупности в процессе выборки остается неизменной. Единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами на следующем шаге отбора вновь попасть в выборку. Повторная выборка в социально-экономической жизни встречается редко.

При бесповторном отборе единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем отборе не участвует. Таким образом, при бесповторном отборе численность единиц генеральной совокупности сокращается в процессе выборки.

2. Отбор может быть организован как :
- собственно-случайный;
- механический;
- стратифицированный (типический);
- серийный
Собственно-случайный отбор – такой отбор единиц из генеральной совокупности, когда на включение (исключение) единицы в выборку (из выборки) не может повлиять какой-либо фактор кроме случая. Технически он осуществляется посредством жеребьевки или таблиц случайных чисел. При этом необходимо иметь список единиц генеральной совокупности.
Примером может служить отбор студентами на экзамене экзаменационных билетов.

Механический отбор - это бесповторный отбор элементов из генеральной совокупности, упорядоченной по нейтральному (несущественному для цели исследования) признаку через равные интервалы. Механический отбор по результатам близок к бесповторному собственно-случайному.
Примеры:
Отбор каждой 20-й детали, сходящей с конвейера для проверки ее качества. Здесь нейтральный признак – номер детали.

При исследовании успеваемости студентов вуза в качестве нейтрального признака можно взять фамилию, имя и отчество студента. Всех студентов упорядочивают по Ф.И.О. После чего отбирают заданное число студентов по фамилиям механически, через определенный интервал.
Размер интервала в генеральной совокупности равен обратному значению доли выборки. Так, при 2%-ой выборке отбирается и проверяется каждая 50-я единица (1/0,02), при 5%-ой выборке – каждая 20-ая единица (1/0,05).

Стратифицированный отбор используют для отбора единиц из неоднородной совокупности, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных групп по существенным для цели исследования признакам. Из каждой такой группы собственно-случайным или механическим способом производится индивидуальный отбор единиц в выборку. Стратифицированный отбор, при котором пропорции между группами в выборке совпадают с пропорциями между группами в генеральной совокупности, называется типическим отбором.

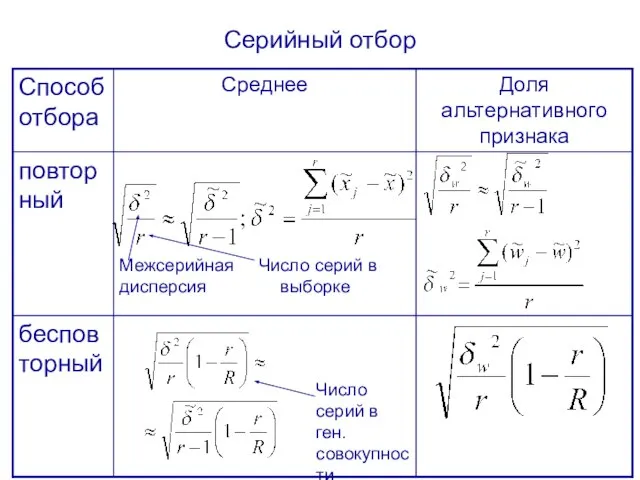
Серийный отбор представляет случайный отбор из генеральной совокупности не отдельных единиц, а их равновеликих групп (серий) с тем, чтобы в таких группах подвергать наблюдению все без исключения единицы.
Серийный отбор применяют в том случае, когда исследуемый признак колеблется внутри серий незначительно.
Применение серийной выборки обусловлено тем, что многие товары для их транспортировки, хранения, продажи упаковываются в пачки, ящики и т.п. Поэтому при контроле качества упакованного товара рациональнее проверить несколько упаковок (серий), чем из всех упаковок отбирать необходимое количество товара.

Выборки также делят на большие (с объемом большим или равным 30 единицам) и малые (с объемом меньше 30 единиц).

ТОЧЕЧНОЕ И ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ
Точечной называют оценку (θ*), которая определяется одним числом. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам.
Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность оценки (величину предельной ошибки выборки) и надежность оценки (вероятность, с которой гарантирован результат оценивания).
Интервальная оценка (θ*-Δ; θ*+Δ) представляет собой доверительный интервал.

Вероятность того, что доверительный интервал не покроет генеральную характеристику (параметр) совокупности обозначают α и называют уровнем значимости: α =1- Рдов.
При Рдов=0,95 α=0,05;
при Рдов=0,99 α=0,01.

Порядок расчета интервальной оценки характеристики (параметра) генеральной совокупности:
1. Определяют точечную оценку характеристики (параметра) генеральной совокупности (θ*).

2. Рассчитывают среднюю ошибку выборки - μ.
Формулы расчета средней ошибки выборки -μ зависят от способа отбора и от вида оцениваемой характеристики генеральной совокупности (среднее или доля).
Собственно –случайный отбор

Механический и типический способы отборы
остаточная (средняя из внутригрупповых) дисперсия выборки

Серийный отбор
Межсерийная Число серий в дисперсия выборке
Число серий в ген.совокупности

3. Рассчитывают предельную ошибку выборки: Δ=t∙μ, При большом объеме выборки (≥30) значение коэффициента доверия t находим из таблиц интегральной функции стандартного нормального распределения по заданной доверительной вероятности Рдов.
При небольшом объеме выборки (n<30) значение t определяют по таблицам интегральной функции распределения Стьюдента.
(Значение t по таблицам Стьюдента будет чуть больше, чем по таблицам стандартного нормального распределения.)

4. Определяют границы доверительного интервала:
(θ*-Δ; θ*+Δ) – интервальная оценка.
Вывод: с вероятностью Рдов данный интервал покроет генеральную характеристику (параметр).

Пример 1: Из партии готовой продукции в порядке механической выборки проверено 50 лампочек на продолжительность горения. Средняя продолжительность горения лампочки оказалась равной 840 ч. при среднем квадратическом отклонении 60 ч.
С вероятностью 0,95 определить доверительные пределы средней продолжительности горения лампочки в генеральной совокупности (партии продукции).
РЕШЕНИЕ:
Для построения доверительного интервала (θ*-Δ; θ*+Δ) в качестве точечной оценки θ* возьмем выборочное среднее арифметическое. По условию оно равно 840 ч.
Чтобы рассчитать предельную ошибку Δ=t∙μ нужно определить среднюю ошибку μ. В случае механического отбора и оценке среднего воспользуемся формулой:

Значение t найдем по таблицам стандартного нормального распределения, так как в нашем случае выборка большая (ее объем равный 50 > 30). Для Рдов=0,95 по таблице стандартного нормального распределения t=1,96.
Тогда Δ=1,96∙8,6 = 16,86 (ч.). То есть с вероятностью 0,95 можно утверждать, что средняя продолжительность горения лампочки в нашей выборке отличается от этой же характеристики в генеральной совокупности не более чем на 16,6 часа.
Теперь можем построить доверительный интервал:
(840 – 16,86; 840 + 16,86) или (823,14; 856,86).
Вывод: с вероятностью 0,95 можно утверждать, что средняя продолжительность горения в генеральной совокупности (т.е. во всей партии) не выйдет за пределы от 823 ч. до 857 ч.

Пример 2: За некоторый период времени рабочий изготовил 2000 деталей. Выборочно (методом собственно-случайного бесповторного отбора) проверено 120 деталей. Оказалось, что из них 4 бракованные. Требуется с вероятностью 0,90 определить доверительные пределы доли бракованных деталей среди всех изготовленных рабочим за этот период (т.е. в генеральной совокупности).
РЕШЕНИЕ:
В данном случае требуется построить доверительный интервал для доли альтернативного признака (w). точечной оценкой показателя доли является выборочная доля:
То есть среди проверенных деталей 0,033 (или 3,3%) оказалось бракованных.

Для определения границ доверительного интервала нам нужно найти предельную ошибку Δ, а чтобы найти Δ требуется определить среднюю ошибку μ.
Формула расчета в данном случае (собственно-случайный бесповторный отбор; характеристика – доля):
То есть в среднем отклонение выборочной доли от генеральной составит 0,016.
Теперь найдем коэффициент доверия t по таблице стандартного нормального распределения, т.к. выборка большая (n=120>30). Для Рдов=0,90 t=1,64.

Тогда Δ=1,64∙0,016 = 0,026. Теперь можем построить доверительный интервал: (0,03 – 0,026; 0,03 + 0,026) или (0,004; 0,056).
Вывод: с вероятностью 0,9 можно утверждать, что доля бракованных деталей в общем объеме изготовленных рабочим (в генеральной совокупности) будет в пределах от 0,004 до 0,056 или от 0,4% до 5,6%

Другая задача, решаемая с помощью выборочного метода: определение необходимого объема выборки - n при заданной точности (Δ) и надежности (Рдов) оценивания.
Формулы расчета для собственно –случайного отбора:
харак-ка повторный отбор бесповторный отбор
Среднее
Доля альтернативного признака

Пример 3: На городской телефонной станции в порядке собственно-случайной выборки проводится обследование телефонных разговоров с целью определения сред.продолжительности разговора. Сколько телефонных разговоров требуется обследовать, чтобы с вероятностью 0,95 предельная ошибка (точность) при определении средней продолжительности разговора не превышала 1 мин. (В порядке пробного обследования исправленное среднее квадратическое отклонение длительности разговора составило 5 мин.)
РЕШЕНИЕ: Необходимый объем выборки можно определить по формуле:
Дисперсия (s2) по условию равна 52 = 25. При Рдов=0,95 t=1,96.

Тогда объем выборки будет равен:
Вывод:
96 телефонных разговоров требуется обследовать, чтобы с вероятностью 0,95 предельная ошибка (точность) при определении средней продолжительности разговора не превышала 1 мин.