Содержание
- 2. Постановка задачи Дано: u={u0, u1, … , un} y={y0, y1, … , yn} Найти: y =
- 3. Методы вычисления Интерполяция Аппроксимация
- 4. Интерполяция функций Интерполяционная формула сопоставляет с функцией функцию известного класса , зависящую от параметров , выбранных
- 5. Интерполяционная функция Лагранжа
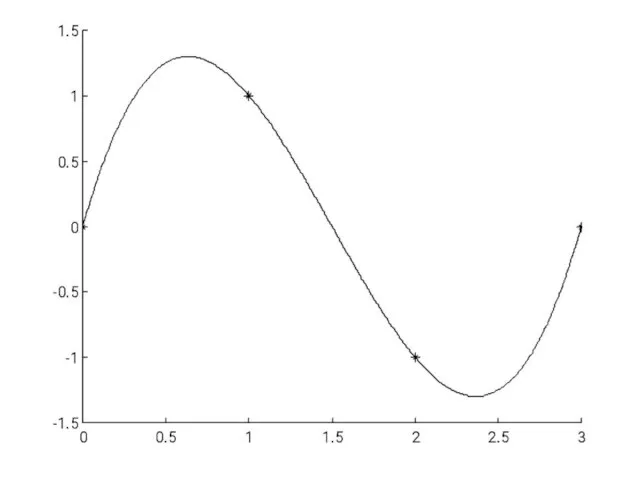
- 6. Пример 1: Пусть: u={0, 1, 2, 3} y={0, 1, -1, 0} Тогда:
- 8. Интерполяционная функция Ньютона
- 9. Пример 2: Пусть: u={0, 1, 2, 3} y={0, 1, -1, 0} Тогда:
- 11. Аппроксимация функциональных зависимостей
- 12. Решение задачи аппроксимации
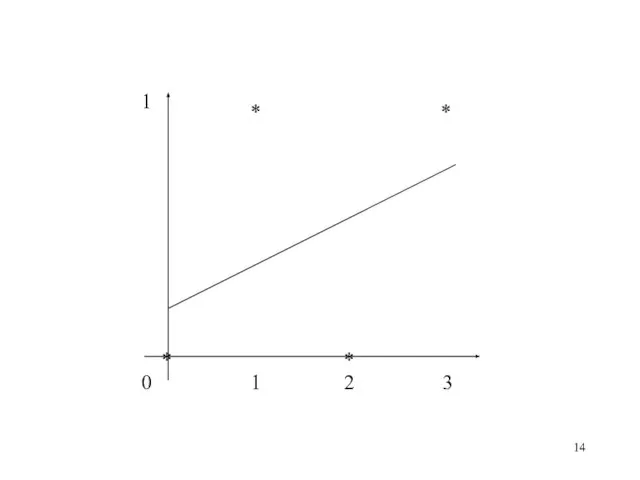
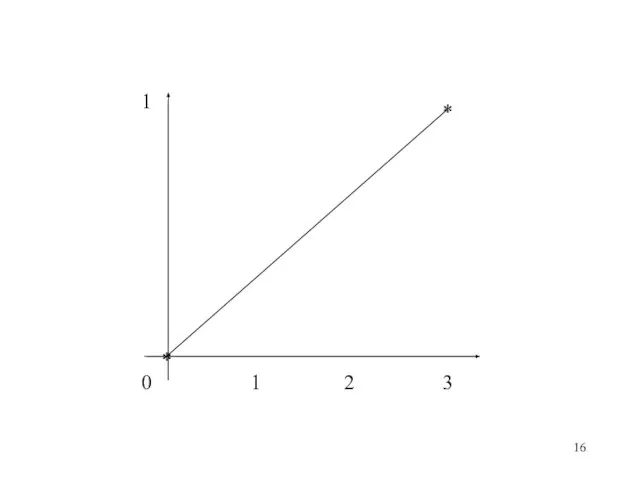
- 13. Пример 3: Пусть: u={0, 1, 2, 3}, y={0, 1, 0, 1}, ϕ=[1,u]T Тогда:
- 15. * * * 1 0 1 2 3
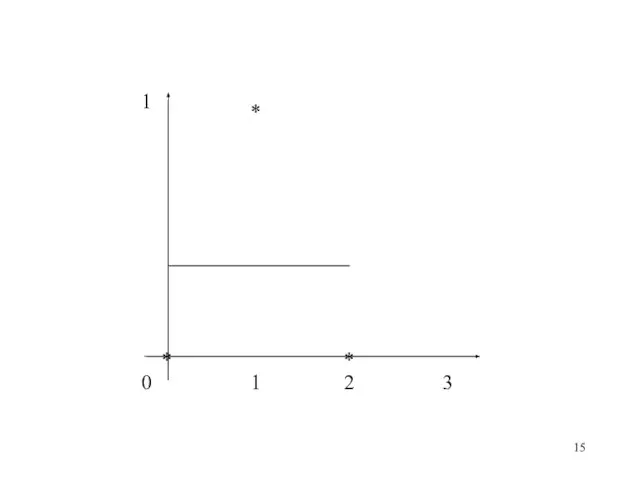
- 16. * * 1 0 1 2 3
- 18. Скачать презентацию







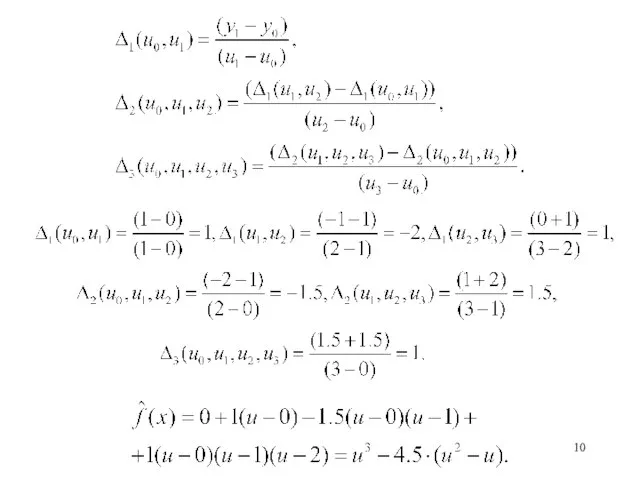


![Пример 3: Пусть: u={0, 1, 2, 3}, y={0, 1, 0, 1}, ϕ=[1,u]T Тогда:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/380647/slide-12.jpg)
 Назови пословицу
Назови пословицу Современные средства поражения
Современные средства поражения Аладин, тренажер
Аладин, тренажер Парки Москвы собирают друзей!
Парки Москвы собирают друзей! Моя семья в годы войны
Моя семья в годы войны Как подготовить современный урок
Как подготовить современный урок Презентация на тему Анненский Иннокентий Федорович
Презентация на тему Анненский Иннокентий Федорович  Открытия российского кинематографа
Открытия российского кинематографа УХИЛЕННЯ ВІД ПОДАТКІВ І ПЕРЕКЛАДАННЯ ПОДАТКІВ
УХИЛЕННЯ ВІД ПОДАТКІВ І ПЕРЕКЛАДАННЯ ПОДАТКІВ Презентация "Парламентские слушания по вопросу о налогах" - скачать презентации по Экономике
Презентация "Парламентские слушания по вопросу о налогах" - скачать презентации по Экономике Живопись на рубеже XIX-XX веков
Живопись на рубеже XIX-XX веков структура
структура ЛЕКЦИЯ Обращения в органы публичной власти, 2022
ЛЕКЦИЯ Обращения в органы публичной власти, 2022 20170202_rkm
20170202_rkm Презентация на тему Константин Бальмонт
Презентация на тему Константин Бальмонт И.А.КРЫЛОВ. БАСНИ
И.А.КРЫЛОВ. БАСНИ А.С. Пушкин “Дубровский” Главы II - IV
А.С. Пушкин “Дубровский” Главы II - IV Тройной прыжок. Легкая атлетика
Тройной прыжок. Легкая атлетика «Героические страницы войны в жизни тружеников тыла Ново-Алексеевского округа»
«Героические страницы войны в жизни тружеников тыла Ново-Алексеевского округа» Таинственные силы природы
Таинственные силы природы Презентация на тему Возрастные особенности учащихся 5-х классов. Преемственность в обучении
Презентация на тему Возрастные особенности учащихся 5-х классов. Преемственность в обучении ЛИЧНАЯ МОТИВАЦИЯ – ОСНОВА ДОБРОВОЛЬЧЕСТВА
ЛИЧНАЯ МОТИВАЦИЯ – ОСНОВА ДОБРОВОЛЬЧЕСТВА Баскетбол
Баскетбол Изучение математической модели иммунной защиты организма
Изучение математической модели иммунной защиты организма  презентация
презентация Тренировочная работа№1
Тренировочная работа№1 Теория эволюции
Теория эволюции 12 июня – День России. Виртуальная выставка
12 июня – День России. Виртуальная выставка