Загальний огляд основних методів та алгоритмів обробки даних

3. Операції із зображеннями: точкові операції

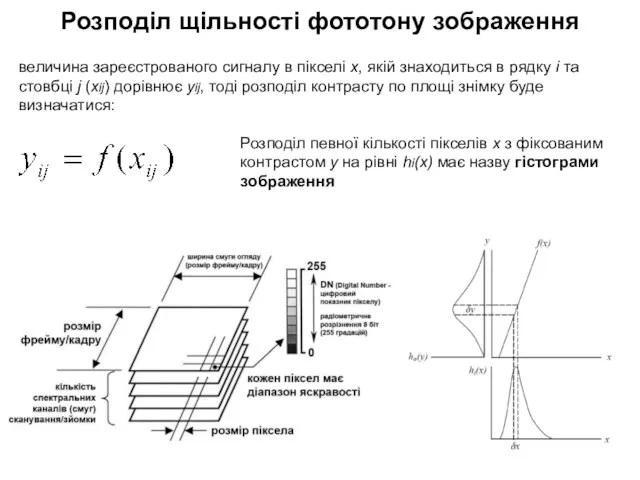
величина зареєстрованого сигналу в пікселі x, якій знаходиться в рядку і та стовбці j (xij) дорівнює yij, тоді розподіл контрасту по площі знімку буде визначатися:
Розподіл певної кількості пікселів x з фіксованим контрастом y на рівні hi(x) має назву гістограми зображення
Розподіл щільності фототону зображення

Терміни та визначення
ГІСТОГРАМА - функція, визначена на множині значень яскравості, областю значень якої є додатні цілі числа. Значенням функції f(L) у деякій точці є частота появи значення, яскравості, тобто кількість елементів (пікселів) зображення, які мають значення яскравості L

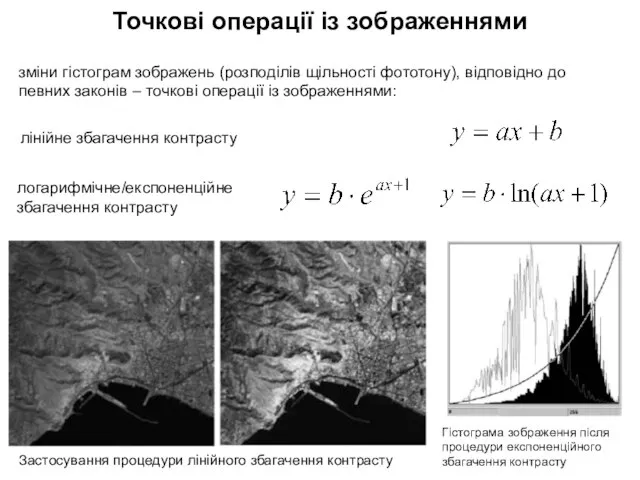
Точкові операції із зображеннями
зміни гістограм зображень (розподілів щільності фототону), відповідно до певних законів – точкові операції із зображеннями:
лінійне збагачення контрасту
логарифмічне/експоненційне збагачення контрасту
Застосування процедури лінійного збагачення контрасту
Гістограма зображення після процедури експоненційного збагачення контрасту

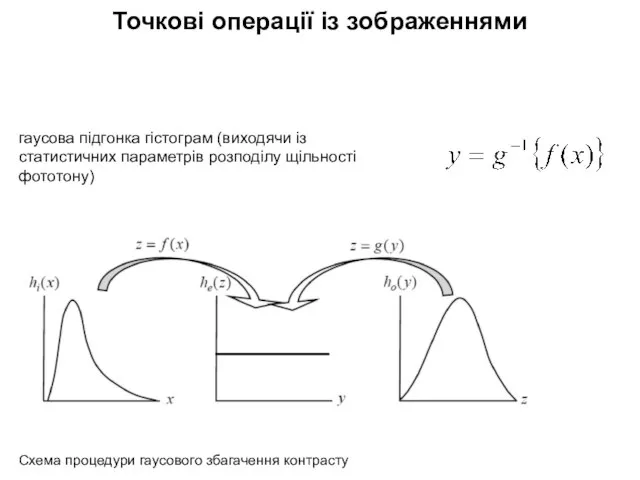
Точкові операції із зображеннями
Схема процедури гаусового збагачення контрасту
гаусова підгонка гістограм (виходячи із статистичних параметрів розподілу щільності фототону)

балансові методи збагачення контрасту
Зображення Landsat ETM після застосування процедури балансового збагачення контрасту за параболічним законом (Balance Contrast Enhancement Technique - BCTE)
Точкові операції із зображеннями

3. Операції із зображеннями: алгебраїчні операції

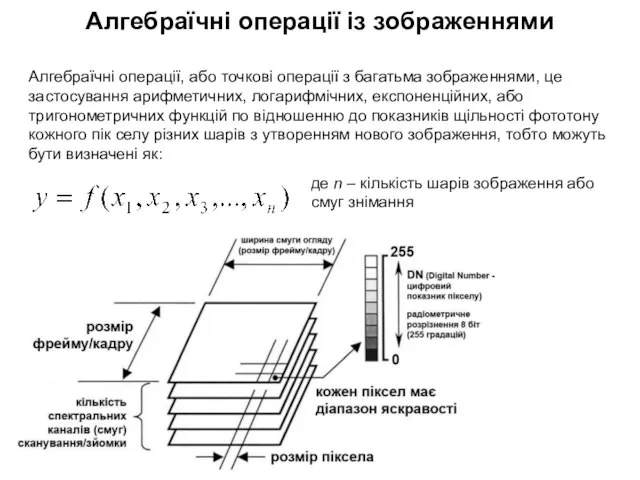
Алгебраїчні операції із зображеннями
Алгебраїчні операції, або точкові операції з багатьма зображеннями, це застосування арифметичних, логарифмічних, експоненційних, або тригонометричних функцій по відношенню до показників щільності фототону кожного пік селу різних шарів з утворенням нового зображення, тобто можуть бути визначені як:
де n – кількість шарів зображення або смуг знімання

Алгебраїчні операції із зображеннями
додавання зображень
де w – вагові коефіцієнти, k - масштабний фактор
віднімання зображень
Віднімання зображень Landsat TM: a) TM3-TM1 (глина); b) TM4-TM3 (рослинність); c) TM5-TM7 (оксиди заліза); d) композиція RGB = abc

Алгебраїчні операції із зображеннями
множення зображень
Множення зображень Landsat TM: a) результат класифікації вхідного зображення; b) результат множення а) на розподіл інтенсивності вхідного зображення

Алгебраїчні операції із зображеннями
ділення зображень
Ділення зображень Landsat TM: a) TM3/TM1; b) TM4/TM3; c) TM5/TM7; d) композиція RGB = abc

Алгебраїчні операції із зображеннями
стандартизація по спектральним каналам
приведення по логарифмічній різниці

Терміни та визначення
ІНДЕКС – умовний показник, який обчислюється по емпіричній формулі; в результаті арифметичних операцій над яскравостями пікселів космічного зображення (знімку) обчислюється деякий показник (індекс), який дає числову імовірнісну оцінку наявності на поверхні Землі певних речовин, матеріалів (рослинності, мінералів і т. ін.)

Алгебраїчні операції із зображеннями
отримання спектральних індексів і кероване покращення якості
нормалізований диференційний вегетаційний індекс
індекс відношення оксиду заліза
Крім того, вивчають розподіл сигналу на зображенні по відношенню до стандартного спектру випромінювання (сонячного чи модельних поверхонь), а також по відношенню до стандартизованих даних спостережень (наприклад, по відношенню до ETM, ASTER, MODIS тощо)

Спектральний індекс відношення глини за даними Landsat TM
Спектральний індекс відношення оксиду заліза за даними Landsat TM
Спектральні індекси

4. Просторово - частотні методи обробки зображень: фільтрація зображень

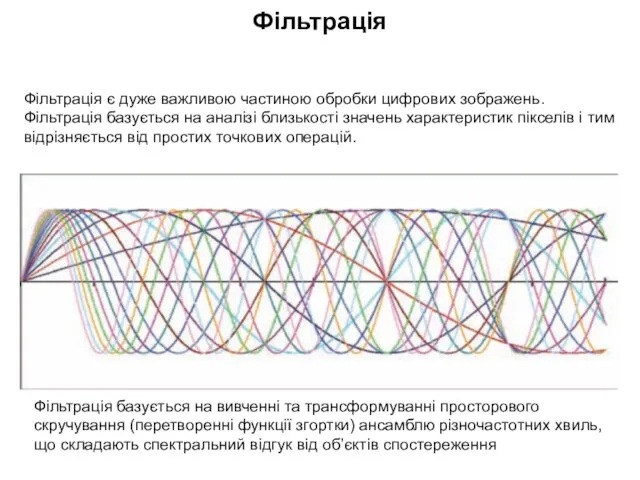
Фільтрація є дуже важливою частиною обробки цифрових зображень. Фільтрація базується на аналізі близькості значень характеристик пікселів і тим відрізняється від простих точкових операцій.
Фільтрація базується на вивченні та трансформуванні просторового скручування (перетворенні функції згортки) ансамблю різночастотних хвиль, що складають спектральний відгук від об’єктів спостереження
Фільтрація

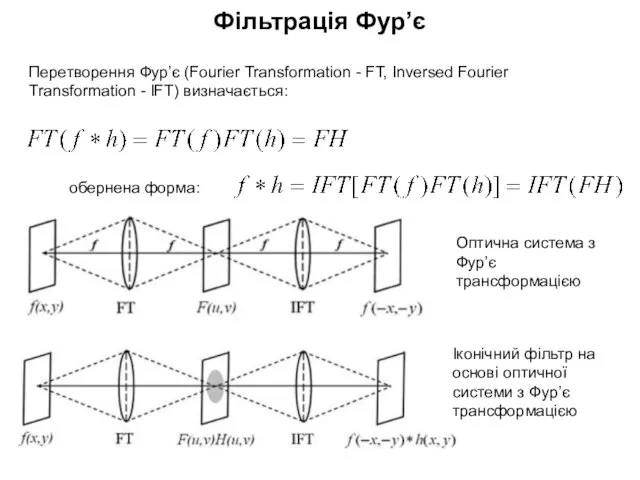
Оптична система з Фур’є трансформацією
Іконічний фільтр на основі оптичної системи з Фур’є трансформацією
Перетворення Фур’є (Fourier Transformation - FT, Inversed Fourier Transformation - IFT) визначається:
Фільтрація Фур’є
обернена форма:

Вхідне зображення f(x, y)
Частотний спектр Фур’є F (u, v)
Фільтрація Фур’є
також можна записати:
Класична фільтрація базується на теоремі згортці, яка визначає властивості Фур’є – фільтрації для оптичних систем – згортку розподілу пікселів зображення f (x, y) та функцію точкового розподілу (point spread function – PSF, або гістограму) зображення h (x, y) як:

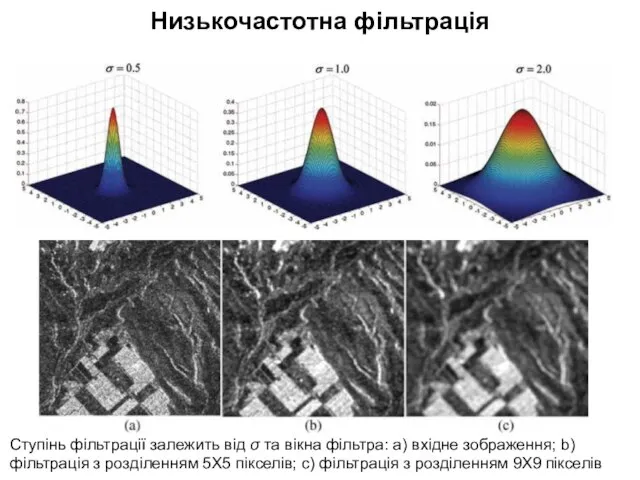
Низькочастотна фільтрація
Низькочастотна фільтрація (low-pass filters / smoothing) або згладжування використовуються для видалення з цифрових зображень високочастотних компонент спектру і таким чином, видалення шуму, при цьому, однак, втрачається детальність.
Основні фільтри: фільтр Гауса, медіанний фільтр, фільтр основної модуляції, умовний згладжувальний фільтр тощо
Фільтр Гауса визначається через стандартне відхилення розподілу фототону зображення σ:

Низькочастотна фільтрація
Ступінь фільтрації залежить від σ та вікна фільтра: а) вхідне зображення; b) фільтрація з розділенням 5Х5 пікселів; c) фільтрація з розділенням 9Х9 пікселів

Високочастотна фільтрація
Високочастотна фільтрація (high-pass filters / edge enhancement) або підкреслювання країв використовується для видалення низькочастотної складової спектру цифрового зображення і, таким чином, підкреслювання ліній зміни контрастів.
Відповідно, цій метод базується на аналізі першої (градієнтна фільтрація) і другої (фільтр Лапласа) похідних розподілу фототону зображень.
градієнтний фільтр:
де
,
- одиничні вектори за напрямами x та y відповідно
фільтр Лапласа:

Високочастотна фільтрація: градієнтний фільтр
Алгоритм градієнтної фільтрації базується на розрахунку простої різниці між показниками розподілу щільності фотонону розрахункового пікселу і сусідніх пік селів у вікні фільтрації, віднесеної до відстаней між ними:
Вхідне зображення а), і результати градієнтної фільтрації: b) gx, c) gy

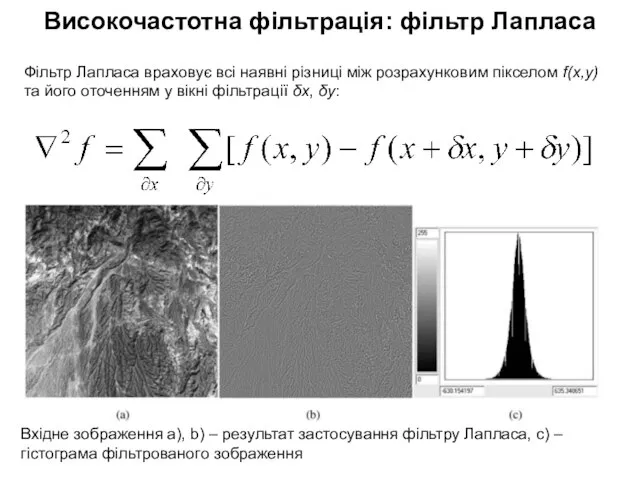
Високочастотна фільтрація: фільтр Лапласа
Фільтр Лапласа враховує всі наявні різниці між розрахунковим пікселом f(x,y) та його оточенням у вікні фільтрації δx, δy:
Вхідне зображення а), b) – результат застосування фільтру Лапласа, с) – гістограма фільтрованого зображення

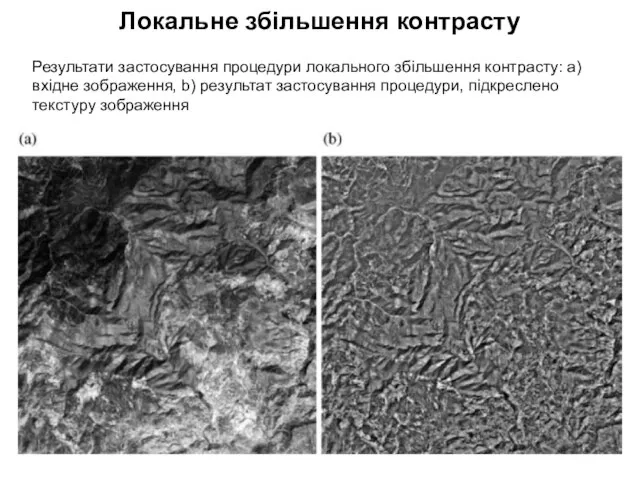
Локальне збільшення контрасту
Ця процедура базується на значенні статистичних показників розподілів щільності фототону зображень.
В найпростішому випадку використовується середнє значення по віконцю фільтрації та загальне середнє m0:
Існують інші алгоритми, що використовують додаткові статистичні показники (стандартне відхилення σ) та можливості параметричного контролю (параметр α):

Локальне збільшення контрасту
Результати застосування процедури локального збільшення контрасту: а) вхідне зображення, b) результат застосування процедури, підкреслено текстуру зображення