Слайд 3Эта книга была переведена на языки многих народов мира, а сама геометрия,

изложенная в ней, стала называться евклидовой геометрией.
В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств: массы, цвета и т. д. Отвлекаясь от этих свойств и беря во внимание только форму и размеры предметов, мы приходим к понятию геометрической фигуры.
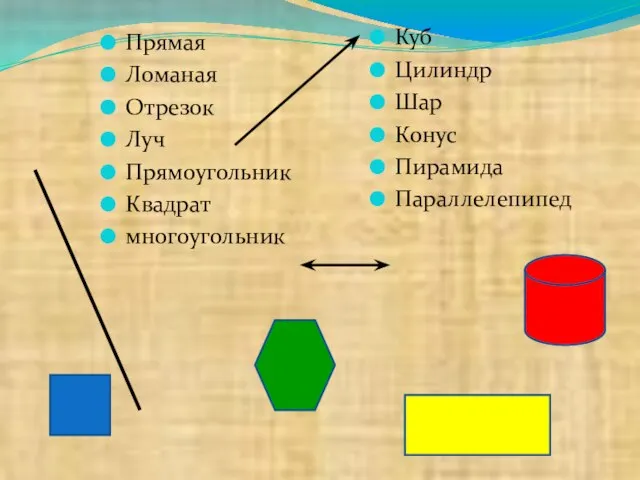
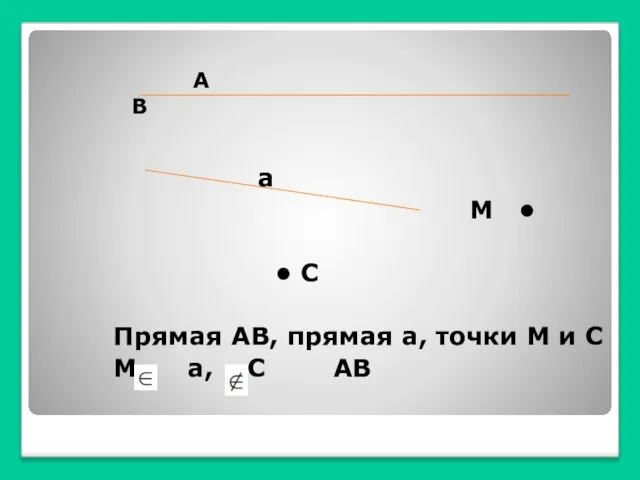
На уроках математики вы познакомились с некоторыми геометрическими фигурами и представляете себе, что такое точка, прямая, отрезок, луч, угол, как они могут быть расположены относительно друг друга. Вы знакомы с такими фигурами, как треугольник, прямоугольник, круг.
Геометрия не только дает представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать, делать выводы, то есть логически мыслить.








 Презентация(проект) на тему:
Презентация(проект) на тему: Юридический клуб Екатеринбурга. Правовая просвещенность. Профессиональный выбор. Гражданская позиция
Юридический клуб Екатеринбурга. Правовая просвещенность. Профессиональный выбор. Гражданская позиция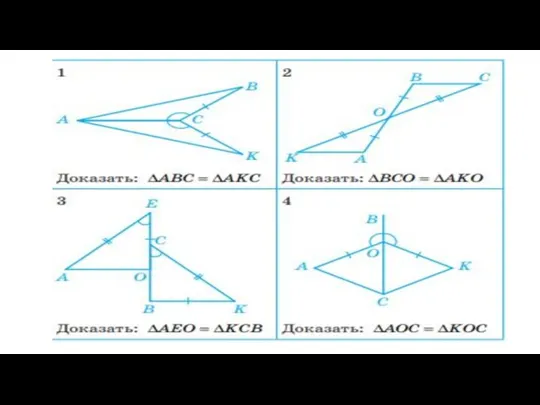 1 признак
1 признак Права собственников участков земли
Права собственников участков земли Автомобилизация России и проблемы регулирования
Автомобилизация России и проблемы регулирования Сиропы. Помада. Кандир. Фруктово-ягодные полуфабрикаты
Сиропы. Помада. Кандир. Фруктово-ягодные полуфабрикаты Презентация на тему Биогеоценоз как особый уровень организации жизни
Презентация на тему Биогеоценоз как особый уровень организации жизни Владимир Иванов, ген. директор PM Consulting Services. - презентация
Владимир Иванов, ген. директор PM Consulting Services. - презентация Пирожное "Пасхальное яйцо"
Пирожное "Пасхальное яйцо" СВЕТЛОЕ ХРИСТОВО ВОСКРЕСЕНИЕ
СВЕТЛОЕ ХРИСТОВО ВОСКРЕСЕНИЕ Редкие насекомые нуждающиеся в охране
Редкие насекомые нуждающиеся в охране Нагрев проводников и электрических аппаратов. Лекция 11
Нагрев проводников и электрических аппаратов. Лекция 11 PCI DSS в Украине К чему готовиться?
PCI DSS в Украине К чему готовиться? Dima_Maria - Use case application of SU2 soft package
Dima_Maria - Use case application of SU2 soft package Формирование ключевых компетенций учащихся начальной школы
Формирование ключевых компетенций учащихся начальной школы Внеземная жизнь в кинематографе
Внеземная жизнь в кинематографе Орфографический практикум
Орфографический практикум Lipatova_MA_Prezentatsia (1)
Lipatova_MA_Prezentatsia (1) Семинар «Поиск инвестора и подготовка документов для встречи с ним»
Семинар «Поиск инвестора и подготовка документов для встречи с ним» Возникновение культуры (первобытное общество) (Тема 3)
Возникновение культуры (первобытное общество) (Тема 3) Презентация на тему "УРОК ЗНО Інтернет і ЗНО-2014" - скачать презентации по Педагогике
Презентация на тему "УРОК ЗНО Інтернет і ЗНО-2014" - скачать презентации по Педагогике Отчёт директора МБУ ДО ДШИ №1
Отчёт директора МБУ ДО ДШИ №1 The balance sheet
The balance sheet Практика внедрения систем безналичного расчёта питания в школах. Создание единой городской информационной системы
Практика внедрения систем безналичного расчёта питания в школах. Создание единой городской информационной системы Какого цвета небо?
Какого цвета небо? Многокомпонентный динамометр
Многокомпонентный динамометр Робер Кампен (1378 – 1444)
Робер Кампен (1378 – 1444) Презентация на тему: Обезьянка-воровка
Презентация на тему: Обезьянка-воровка