Содержание
- 2. ПОСВЯЩАЕТСЯ МАТЕМАТИКАМ Спасибо вам за красоту науки, За ясность цифр, за формулы игру. Решая каждый раз
- 3. Леонардо Фибоначчи родился в городе Пиза, к сожалению историки не сохранили точную дату его рождения. Родился
- 4. ТРУДЫ ЛЕОНАРДО ФИБОНАЧЧИ Фибоначчи создал несколько книг посвященных математическому искусству. В 1202 и 1228 годах вышла
- 5. ЗОЛОТАЯ МАТЕМАТИКА Наверняка вам не раз приходилось задумываться, почему Природа способна создавать такие удивительные гармоничные структуры,
- 6. И все же история донесла до наших дней его главное творение - числовой ряд Фибоначчи уникальности
- 7. РЯД ФИБОНАЧЧИ Ряд Фибоначчи выглядит следующим образом: 0, 1, 1, 2, 3, 5, 8, 13, 21,
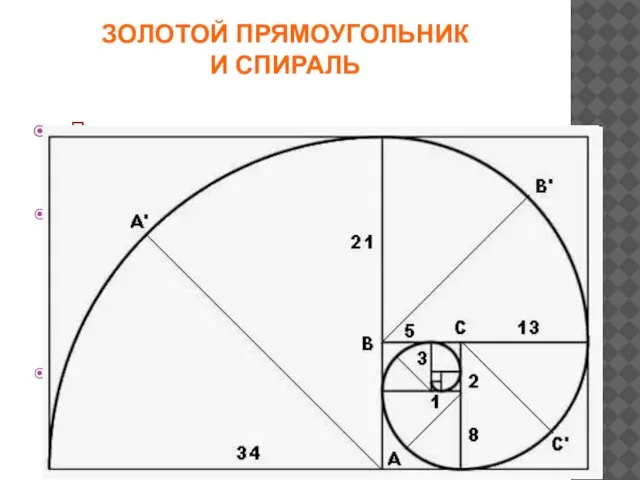
- 8. ЗОЛОТОЙ ПРЯМОУГОЛЬНИК И СПИРАЛЬ Прямоугольник с пропорциями золотого сечения называется идеальный прямоугольник или золотой прямоугольник. Если
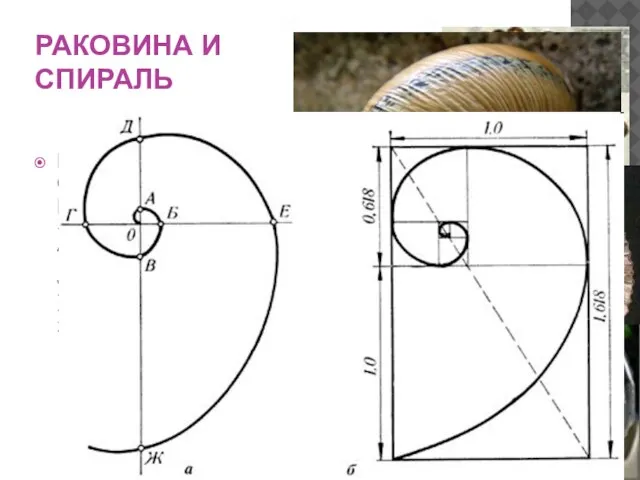
- 9. РАКОВИНА И СПИРАЛЬ Раковина в форме спирали - форма раковины заинтересовала Архимеда и он выяснил, что
- 10. СЕМЕНА И СПИРАЛЬ Семена в подсолнухе, в шишке располагаются так же в виде спирали.
- 11. СПИРАЛЬ И ПАУКИ Пауки плетут свою сеть и стадо на которое нападает хищник, тоже разбегаются по
- 12. РЯД ФИБОНАЧИ И ЯЩЕРИЦА Ящерица – если поделить ящерицу на хвост и тело, то соотношение их
- 13. СООТНОШЕНИЕ ДЛИНЫ РЕБРА ПИРАМИДЫ Пирамиды – длина ребра пирамиды равна 783.3 футам, а высота пирамиды равна
- 14. РЯД ФИБОНАЧЧИ И ГАЛАКТИКА Как видно, числовой ряд Фибоначчи широко представлен в нашей жизни: в строении
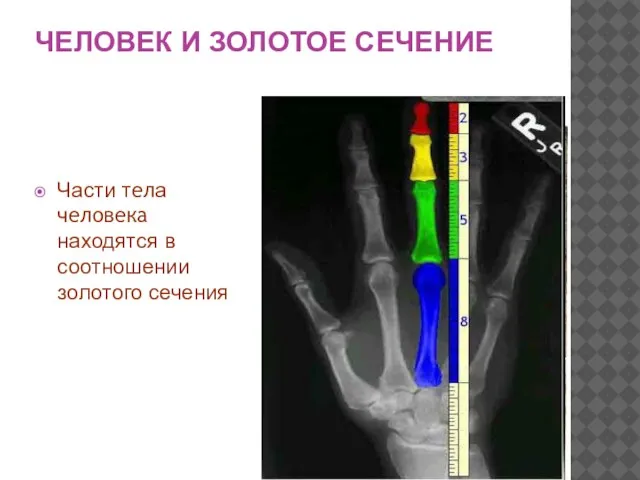
- 15. ЧЕЛОВЕК И ЗОЛОТОЕ СЕЧЕНИЕ Части тела человека находятся в соотношении золотого сечения
- 16. В современной науке существует много научных групп, профессионально изучающих Золотое Сечение, числа Фибоначчи и их многочисленные
- 17. ИСПОЛЬЗУЕМЫЕ РЕСУРСЫ ИНТЕРНЕТА: http://facweb.cs.depaul.edu/sgrais/images/Proportion/0602003.jpg http://im4-tub-ru.yandex.net/i?id=311553490-48-72 http://pthumbnails.5min.com/5036637/251831837_c.jpg http://im4-tub-ru.yandex.net/i?id=171051495-15-72 http://im3-tub-ru.yandex.net/i?id=468196098-32-72 http://img-fotki.yandex.ru/get/4903/corex.14/0_3fc9e_c71ec4b_L http://alemix-forex.ru/биография%20фибоначчи http://im4-tub-ru.yandex.net/i?id=76447688-22-72 http://im7-tub-ru.yandex.net/i?id=136064359-52-72 http://im7-tub-ru.yandex.net/i?id=379143481-36-72 http://im2-tub-ru.yandex.net/i?id=277195420-28-72 http://im8-tub-ru.yandex.net/i?id=355862324-12-72 http://im3-tub-ru.yandex.net/i?id=352682289-01-72
- 18. http://s011.radikal.ru/i316/1104/a1/2daf4ed83765.jpg http://turkmenistan.karakum.net/albums/kamma/7-plugin-to/?vob=examples-of-fibonacci-sequence-in-art-5XDCDqJJY/WYw8b3u0i7rOYRmRyzfqSAkGK0iX3x3pZ2NxhdW2/0zoGiHaquhPkd3jnAK7orDtPNIRDk3UhHwOPNbqh4dnvj7HfXec7k1ToN4RNBiNEExHFMtTQuYlk=3e8.jpg http://vova1001.narod.ru/images/00006157.jpg http://kartcent.ru/zagadka-chisel-fibonachchi/ http://i5.pixs.ru/storage/9/0/3/3jpg_7040654_3032903.jpg http://im7-tub-ru.yandex.net/i?id=464665397-05-72 http://im3-tub-ru.yandex.net/i?id=69997937-33-72 http://im4-tub-ru.yandex.net/i?id=240120133-59-72 http://im5-tub-ru.yandex.net/i?id=496247041-60-72 http://www.cio.arcticsu.ru/projects/pr1620/_derived/index.htm_cmp_radial010_bnr.gif
- 20. Скачать презентацию














 Высокий рейтинг успеваемости. Победы на олимпиадах и конкурсах. Высокая социальная активность. Победа в творческих конкурсах. Исс
Высокий рейтинг успеваемости. Победы на олимпиадах и конкурсах. Высокая социальная активность. Победа в творческих конкурсах. Исс Термическая обработка. Отжиг
Термическая обработка. Отжиг Структура организации современных Вооруженных Сил
Структура организации современных Вооруженных Сил Кавказ
Кавказ Институт правового положения личности в римском праве
Институт правового положения личности в римском праве Использование здоровьесберегающих технологий в психологическом сопровождении учащихся групп особого внимания в условиях школьн
Использование здоровьесберегающих технологий в психологическом сопровождении учащихся групп особого внимания в условиях школьн Особенности управления командой как человеческим ресурсом. Тема 2
Особенности управления командой как человеческим ресурсом. Тема 2 Не кури!
Не кури! Образование и наука
Образование и наука Моя самая любимая книга
Моя самая любимая книга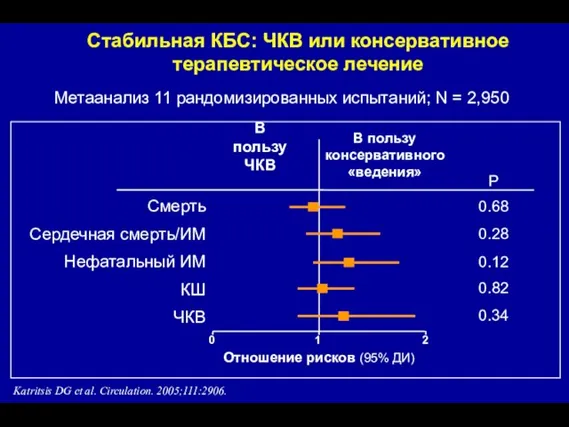 Стабильная КБС: ЧКВ или консервативноетерапевтическое лечение
Стабильная КБС: ЧКВ или консервативноетерапевтическое лечение Практическое применение данных о цитировании в российских университетах и научных организациях
Практическое применение данных о цитировании в российских университетах и научных организациях Презентация на тему winter зима
Презентация на тему winter зима Внешнеполитические связи России с Европой и Азией в конце -XVI в. - начале XVII в
Внешнеполитические связи России с Европой и Азией в конце -XVI в. - начале XVII в КОНФИГУРАЦИЯ ДЛЯ ПРЕДПРИЯТИЙАГРОПРОМЫШЛЕННОГО КОМПЛЕКСА
КОНФИГУРАЦИЯ ДЛЯ ПРЕДПРИЯТИЙАГРОПРОМЫШЛЕННОГО КОМПЛЕКСА Природопользование и устойчивое развитие
Природопользование и устойчивое развитие Пищевые добавки
Пищевые добавки Архитектура NET приложений
Архитектура NET приложений Политический анализ и политическое прогнозирование
Политический анализ и политическое прогнозирование  Организационные структуры маркетинговых служб предприятий питания
Организационные структуры маркетинговых служб предприятий питания Презентация на тему Saint-Petersbourg
Презентация на тему Saint-Petersbourg Велосипедные походы и безопасность туристов
Велосипедные походы и безопасность туристов Коррупция. Викторина
Коррупция. Викторина Борьба с пылью в подготовительном забое
Борьба с пылью в подготовительном забое Конституция РК 1995 года, как основной закон государства
Конституция РК 1995 года, как основной закон государства Виртуальный музей. Российское движение школьников
Виртуальный музей. Российское движение школьников Особливості ЗНО - 2021
Особливості ЗНО - 2021 Главы из книги пророка Осии
Главы из книги пророка Осии