Слайд 2Содержание
Понятие золотого сечения
‘’Золотой’’ треугольник
‘’Золотой’’ прямоугольник
Золотое сечение отрезка
Пятиконечная

звезда - пентаграмма
Золотое сечение в ботанике
Золотое сечение в искусстве
Золотое сечение в анатомии
Золотое сечение в скульптуре
Золотое сечение в современной архитектуре
Золотое сечение в древней архитектуре
Заключение
Слайд 3Золотое сечение – это деление отрезка, при котором длина всего отрезка так

относится к длине его большей части, как длина большей части к меньшей, это соотношение приблизительно равно 0,618.
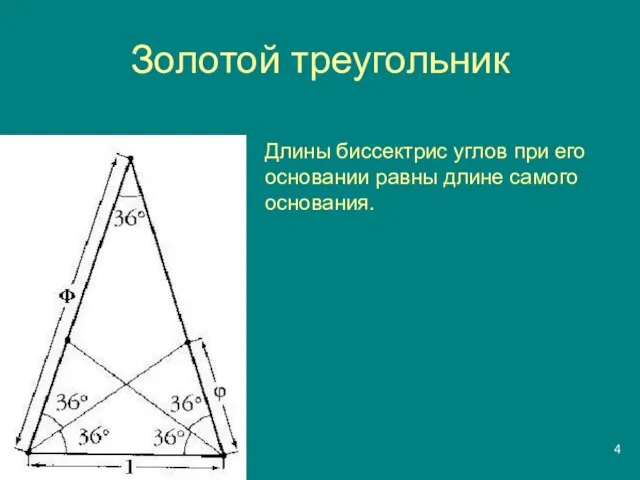
Слайд 4Золотой треугольник
Длины биссектрис углов при его основании равны длине самого основания.
Слайд 5Золотой прямоугольник
Если от прямоугольника отрезать квадрат, опять останется “золотой” прямоугольник, и этот
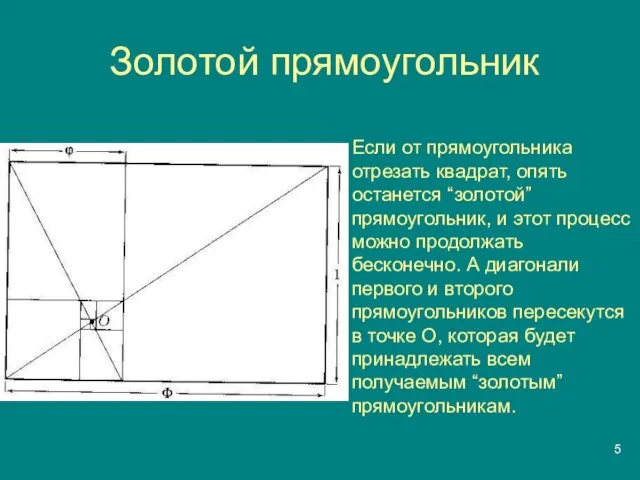
процесс можно продолжать бесконечно. А диагонали первого и второго прямоугольников пересекутся в точке О, которая будет принадлежать всем получаемым “золотым” прямоугольникам.
Слайд 6Золотое сечение отрезка АВ
Золотое сечение отрезка АВ, выполненное с помощью циркуля и
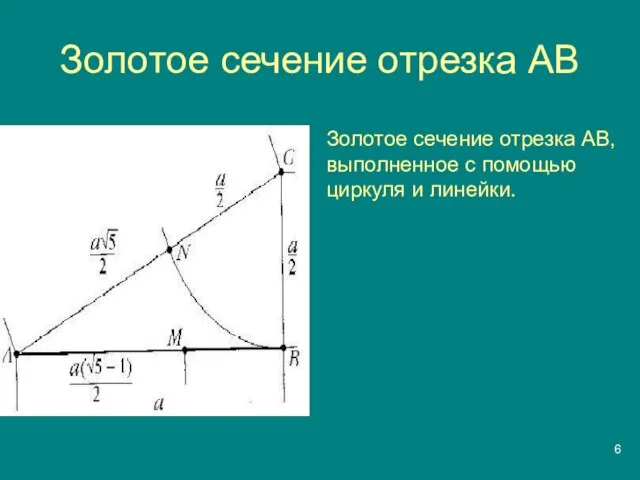
линейки.
Слайд 7Пятиконечная звезда
Каждый конец пятиугольной звезды представляет собой “золотой” треугольник. Его стороны образуют

угол 36° при вершине, а основание, отложенное на боковую сторону, делит её в пропорции золотого сечения.
Слайд 8Золотое сечение в ботанике
Рассматривая расположение листьев на стебле растений, можно заметить, что

между каждыми двумя парами листьев третья расположена в месте золотого сечения.
Слайд 9Золотое сечение в искусстве
Портрет Монны Лизы (Джоконды) основан на “золотых” треугольниках, являющихся

частями правильного звёздчатого пятиугольника.
Слайд 10Золотое сечение в анатомии
Рост человека делится в золотых пропорциях линией пояса, а
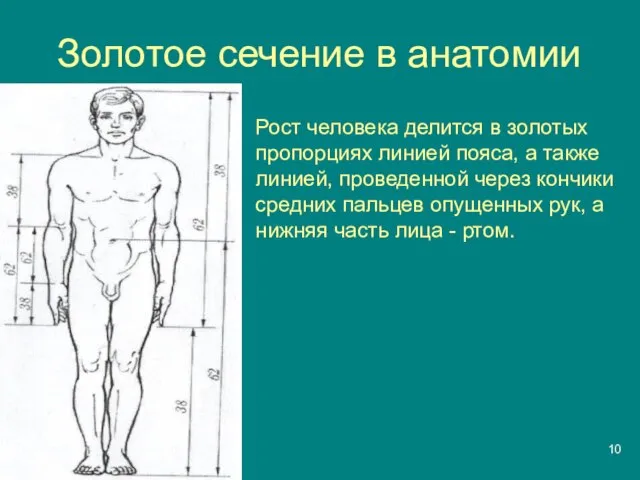
также линией, проведенной через кончики средних пальцев опущенных рук, а нижняя часть лица - ртом.
Слайд 11Золотое сечение в скульптуре
Золотая пропорция статуи Аполлона: рост изображенного человека делится пупочной

линией в золотом сечении.
Слайд 12Золотое сечение в древней архитектуре
12
Парфенон имеет 8 колонн по коротким сторонам и

17 по длинным. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по золотому сечению, то получим те или иные выступы фасада.
Слайд 13 Золотое сечение в современной архитектуре
Пропорции Покровского собора на Красной площади в

Москве определяются восемью членами ряда золотого сечения. Многие члены этого ряда повторяются в затейливых элементах храма многократно.












 Сохранение психологического здоровья учащихся и учителей
Сохранение психологического здоровья учащихся и учителей Земля Earth
Земля Earth Поэма Лермонтова Демон в картинах Михаила Врубеля
Поэма Лермонтова Демон в картинах Михаила Врубеля Капсула культуры
Капсула культуры VI школьная конференция исследовательских и проектных работ учащихся
VI школьная конференция исследовательских и проектных работ учащихся Козьма Прутков
Козьма Прутков Обобщение знаний по теме Зарубежная Европа
Обобщение знаний по теме Зарубежная Европа Металлы в строительстве
Металлы в строительстве Правонарушение и юридическая ответственность
Правонарушение и юридическая ответственность Виды структур управления
Виды структур управления Презентация на тему Дикие животные. Детская энциклопедия
Презентация на тему Дикие животные. Детская энциклопедия 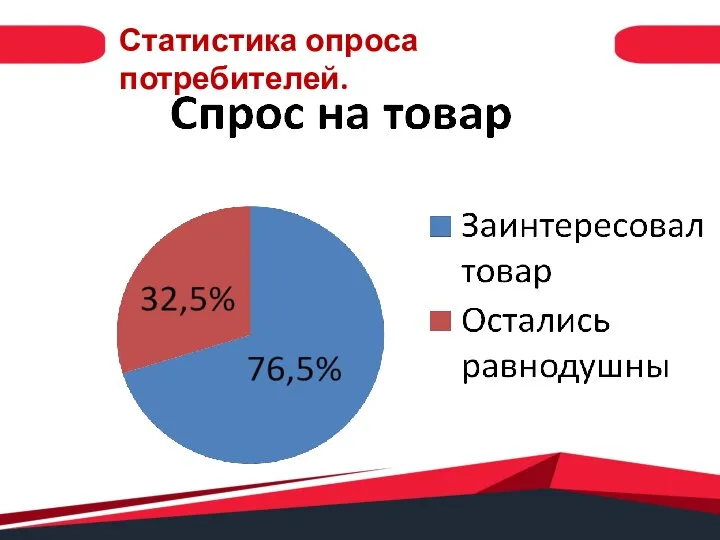 Спрос на товар. Статистика опроса потребителей
Спрос на товар. Статистика опроса потребителей Страны Восточной Европы
Страны Восточной Европы Современная модель музыкального воспитания детей
Современная модель музыкального воспитания детей Funny pancake day quiz
Funny pancake day quiz Рабочая документация классного руководителя
Рабочая документация классного руководителя Классицизм Живопись
Классицизм Живопись Рекомендации по написанию основной общеобразовательной программы дошкольного образовательного учреждения
Рекомендации по написанию основной общеобразовательной программы дошкольного образовательного учреждения Урок № 3. Линейная функция и ее график
Урок № 3. Линейная функция и ее график Художественный ансамбль собора Святого Петра в Риме
Художественный ансамбль собора Святого Петра в Риме WhirlpoolКондиционеры 2011
WhirlpoolКондиционеры 2011 Модель гражданско-патриотического воспитания школьников в условиях сельской малокомплектной школы
Модель гражданско-патриотического воспитания школьников в условиях сельской малокомплектной школы Свойства прямоугольного параллелепипеда
Свойства прямоугольного параллелепипеда Baby O детское очищающее молочко
Baby O детское очищающее молочко Опыт Австралии по освоению месторождений полезных ископаемых на территориях с трудными природными условиями
Опыт Австралии по освоению месторождений полезных ископаемых на территориях с трудными природными условиями Как написать эссе на немецком языке?
Как написать эссе на немецком языке? Виды энергий
Виды энергий 1C:ПРЕДПРИЯТИЕ 8.0
1C:ПРЕДПРИЯТИЕ 8.0