Содержание
- 2. Цель работы: выяснить происхождение обыкновенной дроби
- 3. Обыкновенная дробь числитель знаменатель Смешанное число: Правильная дробь Неправильные дроби целое , ,
- 4. Древние математические документы Кожаный свиток г.Фивы 1700гг. Папирус Ринда написан (1849-1801г. до н.э.), переписан писцом Ахмесом
- 5. Появление первых словесных дробей-долей: «Половина», «десятина», «осьмина», «ломаная»… Простейшие дроби: 1/2, 1/4, 2/3, 3/4 описывали больше
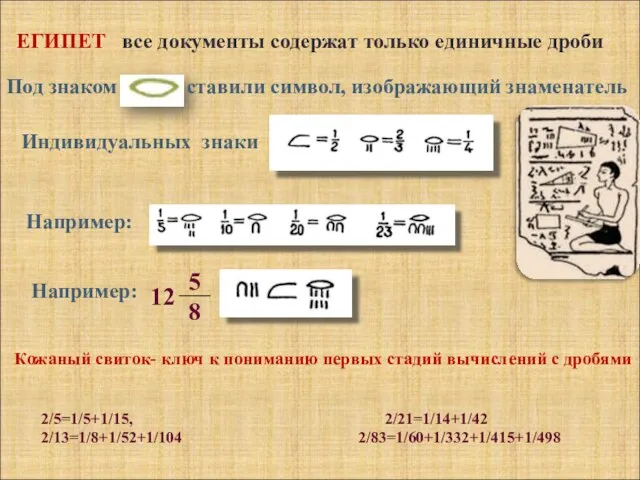
- 6. ЕГИПЕТ все документы содержат только единичные дроби Под знаком ставили символ, изображающий знаменатель Индивидуальных знаки Например:
- 7. ВАВИЛОН ПРИМЕНЯЛИ ШЕСТИДЕСЯТЕРИЧНЫЕ ДРОБИ Доли шестидесятые были привычны для вавилонян: 1/60, 1/3600, 1/603 В Вавилоне письменная
- 8. 1/12…………..... .1 унция 2/12……………. .2 унции 3/12 …….. 3 унции = четверть 4/12 ……. 4 унции
- 9. Греция Греки употребляли египетские и шестидесятеричные дроби. К V в. до н.э. греки умели производить все
- 10. КИТАЙ В древних текстах дробь записывали по схеме « n-ых m». Сначала выполняется деление основной единицы
- 11. Индия В Индии дроби известны очень давно. Ещё в середине II тысячелетия до н.э. упоминаются такие
- 12. ИСЛАМ Дроби в арабской математике считались такими же числами, как и натуральные числа. Записывали их вертикально,
- 13. ЕВРОПА Учение о дробях считалось самым трудным разделом арифметики. Трудность изучения дробей в средневековых школах объяснялась
- 14. На РУСИ 1/4 – четь 1/2 - половина, полтина 1/8 – полчеть 1/16 – полполчеть 1/32
- 15. Появление обыкновенных дробей берёт своё начало в Греции, развивается в Индии и уже в Европе приобретает
- 17. Скачать презентацию













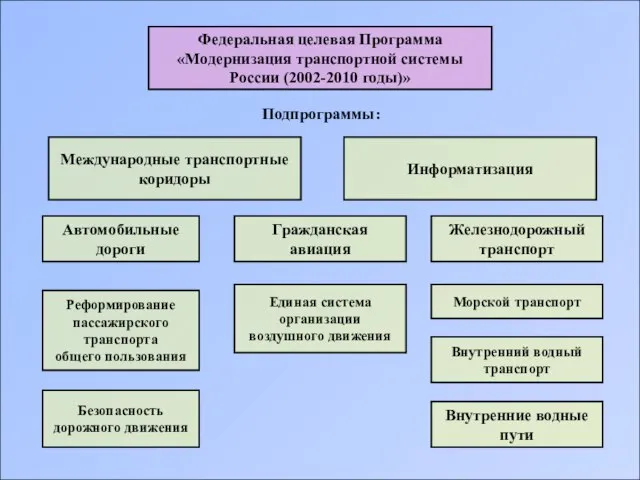 Федеральная целевая Программа «Модернизация транспортной системы России (2002-2010 годы)»
Федеральная целевая Программа «Модернизация транспортной системы России (2002-2010 годы)» Современный учебный процесс, протекающий в условиях информатизации и массовой коммуникации всех сфер общественной жизни, требует
Современный учебный процесс, протекающий в условиях информатизации и массовой коммуникации всех сфер общественной жизни, требует Презентация на тему Понятие и виды таможенной процедуры «таможенный транзит»
Презентация на тему Понятие и виды таможенной процедуры «таможенный транзит»  Лексикографическое описание говора жителей деревни Старые Ирныкши Архангельского района ( проект тематического словаря)
Лексикографическое описание говора жителей деревни Старые Ирныкши Архангельского района ( проект тематического словаря) Китай в средние века
Китай в средние века Измерительные приборы
Измерительные приборы Деятельностный подход на уроках математики
Деятельностный подход на уроках математики Исследование силовой подготовки девушек и женщин, занимающихся фитнесом
Исследование силовой подготовки девушек и женщин, занимающихся фитнесом Презентация на тему Творческая мастерская построения знаний
Презентация на тему Творческая мастерская построения знаний  Сертифікація продуктів тваринного походження на експорт до Євразійського економічного союзу
Сертифікація продуктів тваринного походження на експорт до Євразійського економічного союзу Белик Игорь Вячеславович
Белик Игорь Вячеславович АКАДЕМИЗМ В РУССКОЙ ЖИВОПИСИ
АКАДЕМИЗМ В РУССКОЙ ЖИВОПИСИ Урок информатики
Урок информатики Самостоятельная работа №9. Безниточные швейные машины
Самостоятельная работа №9. Безниточные швейные машины Формирование умений учиться посредством овладения системой алгоритмических предписаний на уроках математики
Формирование умений учиться посредством овладения системой алгоритмических предписаний на уроках математики Market. Инновационное решение для бизнеса
Market. Инновационное решение для бизнеса Управления их классификация
Управления их классификация АКЦИЯ «ДАВАЙТЕ ПЕРЕПИШЕМСЯ!» 26 ИЮНЯ 2010 ГОДА УЛЬЯНОВСК Ульяновскстат 2010 Тел.: + 7 (8422) 32 33 21.
АКЦИЯ «ДАВАЙТЕ ПЕРЕПИШЕМСЯ!» 26 ИЮНЯ 2010 ГОДА УЛЬЯНОВСК Ульяновскстат 2010 Тел.: + 7 (8422) 32 33 21. Автор: учитель физики и информатики Александрова З.В., МОУ СОШ №5 п. Печенга, Мурманская область, 2009 г.
Автор: учитель физики и информатики Александрова З.В., МОУ СОШ №5 п. Печенга, Мурманская область, 2009 г. Crown Jewels
Crown Jewels ИСПОЛЬЗОВАНИЕ ДИСТАНЦИОННОГО КУРСА ДЛЯ ПОДДЕРЖКИ ОЧНЫХ ЗАНЯТИЙ НА КАФЕДРЕ БИОХИМИИ МЕДИЦИНСКОГО ВУЗА С.М.Ершиков Кафедра биоло
ИСПОЛЬЗОВАНИЕ ДИСТАНЦИОННОГО КУРСА ДЛЯ ПОДДЕРЖКИ ОЧНЫХ ЗАНЯТИЙ НА КАФЕДРЕ БИОХИМИИ МЕДИЦИНСКОГО ВУЗА С.М.Ершиков Кафедра биоло Документация на грантовое финансирование молодых ученых по научным и научнотехническим проектам на 2020-2022 годы
Документация на грантовое финансирование молодых ученых по научным и научнотехническим проектам на 2020-2022 годы Эльгарт Габи
Эльгарт Габи Правовые основы установления, исчисления и взимания платы за негативное воздействие на окружающую среду
Правовые основы установления, исчисления и взимания платы за негативное воздействие на окружающую среду Water Drop
Water Drop «Актуальные вопросы организации научно-исследовательской деятельности учащихся» УЧИТЕЛЬ МУНИЦИПАЛЬНОГО КАЗЕННОГО ОБРАЗОВАТЕЛ
«Актуальные вопросы организации научно-исследовательской деятельности учащихся» УЧИТЕЛЬ МУНИЦИПАЛЬНОГО КАЗЕННОГО ОБРАЗОВАТЕЛ Дипломное проектирование - важный этап подготовки специалистов
Дипломное проектирование - важный этап подготовки специалистов Проблемы воспитания
Проблемы воспитания