Линейная функция

Цели:
08.07.2012
Получить навыки построения сложных графиков.
Дать простейшие представления о графиках уравнений.
Научить строить графики.
www.konspekturoka.ru

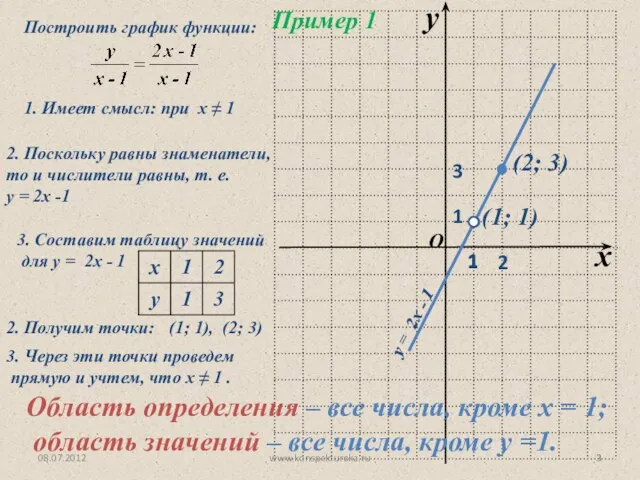
08.07.2012
www.konspekturoka.ru
1. Имеет смысл: при х ≠ 1
2. Поскольку равны знаменатели, то и числители равны, т. е.
у = 2х -1
1
(1; 1)
(2; 3)
у = 2х - 1
3. Составим таблицу значений
для у = 2х - 1
2. Получим точки:
(1; 1), (2; 3)
3. Через эти точки проведем
прямую и учтем, что х ≠ 1 .
Область определения – все числа, кроме х = 1;
область значений – все числа, кроме у =1.

08.07.2012
www.konspekturoka.ru
Имеет смысл: при
х - 1 ≠ 0 (х ≠ 1) х + 2 ≠ 0 (х ≠ -2)
Из обеих частей вычитаем:
Получим:
Умножим обе части на (х + 2):
Получим: у + х = х + 2, или
у = 2
При любом значении аргумента
х значение функции равно одной
и той же величине у = 2.
Точки А(-1; 2), В(2; 2) принадлежат графику функции.
-2
(-2; 2)
(1; 2)
у = 2
Учтем: при х ≠ 1, х ≠ -2
Область определения –
все числа, кроме х = 1, х = -2;
область значений – число у = 2.

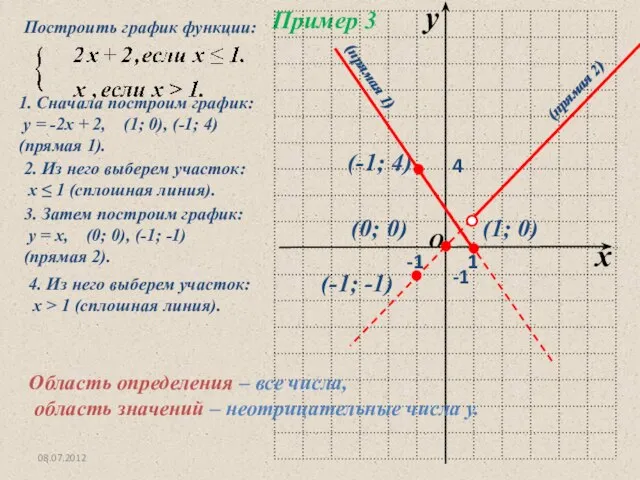
08.07.2012
1. Сначала построим график:
у = -2х + 2, (1; 0), (-1; 4)
(прямая 1).
2. Из него выберем участок:
х ≤ 1 (сплошная линия).
1
(1; 0)
(-1; 4)
(прямая 1)
3. Затем построим график:
у = х, (0; 0), (-1; -1)
(прямая 2).
4. Из него выберем участок:
х > 1 (сплошная линия).
(-1; -1)
(0; 0)
(прямая 2)
Область определения – все числа,
область значений – неотрицательные числа у.

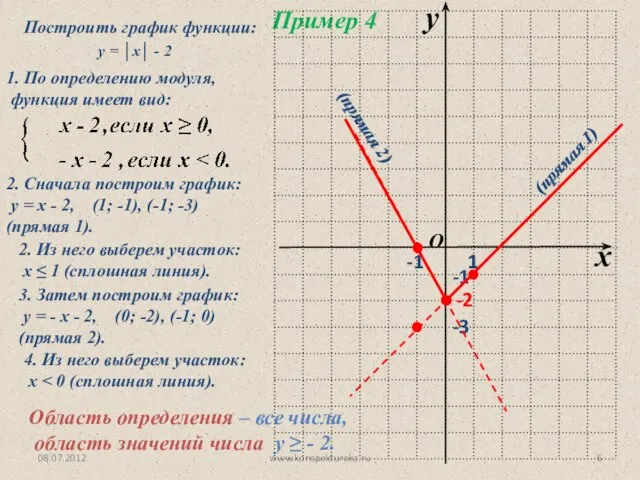
08.07.2012
www.konspekturoka.ru
у = │х│ - 2
2. Сначала построим график:
у = х - 2, (1; -1), (-1; -3)
(прямая 1).
2. Из него выберем участок:
х ≤ 1 (сплошная линия).
(прямая 1)
-2
3. Затем построим график:
у = - х - 2, (0; -2), (-1; 0)
(прямая 2).
(прямая 2)
4. Из него выберем участок:
х < 0 (сплошная линия).
Область определения – все числа,
область значений числа у ≥ - 2.

08.07.2012
www.konspekturoka.ru
Построение уравнения
Вспомним!
Функциональные зависимости (функции)-
зависимости в которых каждому значению
переменной х соответствует только одно
значение переменной у.
В математике встречаются и такие зависимости
между переменными х и у, при которых одному значению х может соответствовать более одного значения у.
В этом случае говорят о графике уравнения.

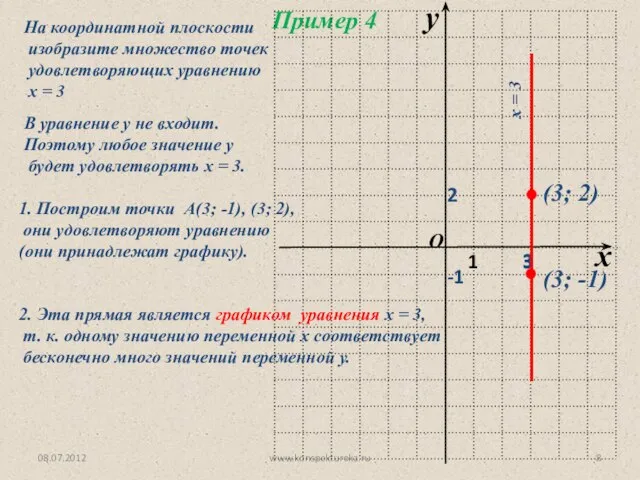
08.07.2012
www.konspekturoka.ru
В уравнение у не входит.
Поэтому любое значение у
будет удовлетворять х = 3.
1. Построим точки А(3; -1), (3; 2),
они удовлетворяют уравнению
(они принадлежат графику).
(3; -1)
х = 3
(3; 2)
2. Эта прямая является графиком уравнения х = 3,
т. к. одному значению переменной х соответствует
бесконечно много значений переменной у.

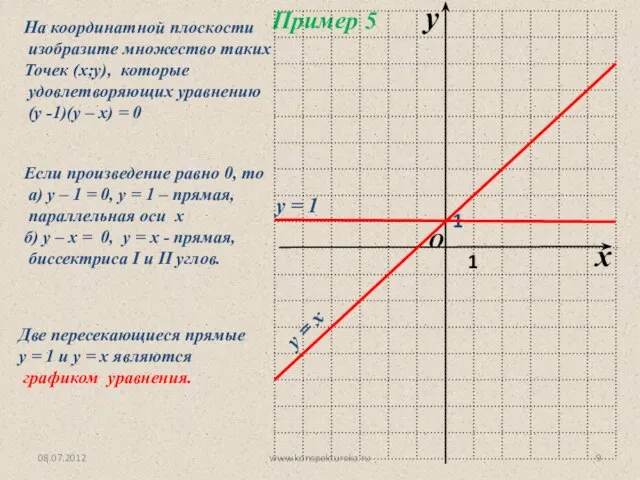
08.07.2012
www.konspekturoka.ru
Если произведение равно 0, то
а) у – 1 = 0, у = 1 – прямая,
параллельная оси х
б) у – х = 0, у = х - прямая,
биссектриса I и II углов.
1
у = 1
у = х
Две пересекающиеся прямые
у = 1 и у = х являются
графиком уравнения.

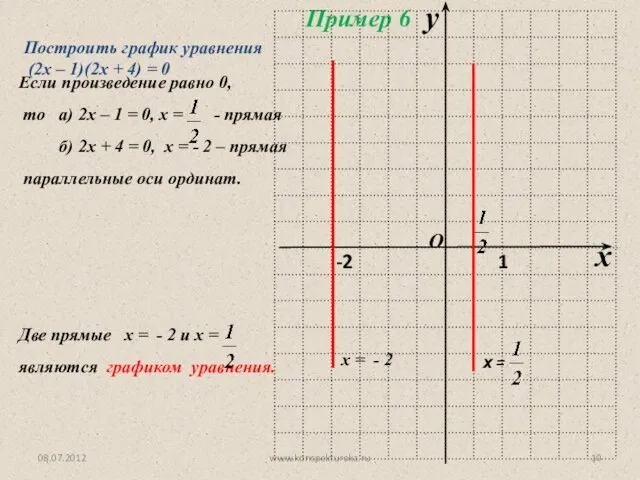
08.07.2012
www.konspekturoka.ru
Построить график уравнения
(2х – 1)(2х + 4) = 0
Пример 6
х = - 2

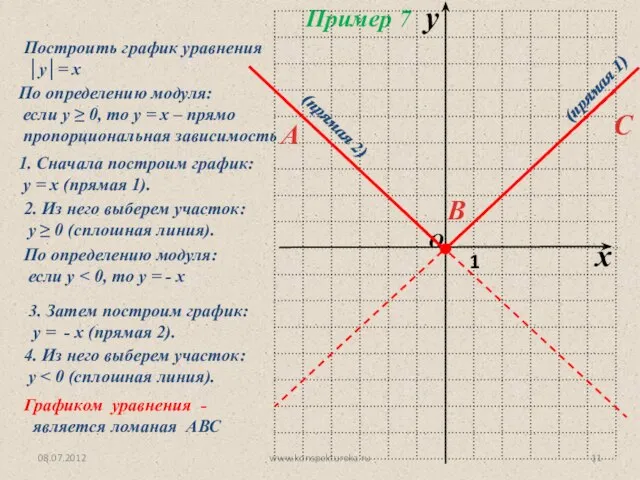
08.07.2012
www.konspekturoka.ru
Построить график уравнения
│у│= х
Пример 7
По определению модуля:
если у ≥ 0, то у = х – прямо
пропорциональная зависимость
1. Сначала построим график:
у = х (прямая 1).
(прямая 1)
2. Из него выберем участок:
у ≥ 0 (сплошная линия).
3. Затем построим график:
у = - х (прямая 2).
(прямая 2)
4. Из него выберем участок:
у < 0 (сплошная линия).
Графиком уравнения -
является ломаная АВС
По определению модуля:
если у < 0, то у = - х

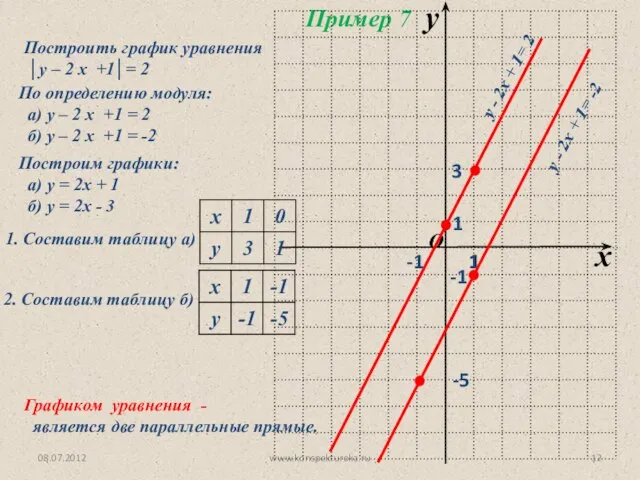
08.07.2012
www.konspekturoka.ru
Построить график уравнения
│у – 2 x +1│= 2
Пример 7
По определению модуля: а) у – 2 x +1 = 2
б) у – 2 x +1 = -2
Построим графики:
а) у = 2х + 1
б) у = 2х - 3
1. Составим таблицу а)
у - 2х + 1= 2
2. Составим таблицу б)
у - 2х + 1= -2
Графиком уравнения -
является две параллельные прямые.