Содержание
- 2. Метод мажорант На самом деле, вы встречались с этим методом, просто не знали, как он называется.
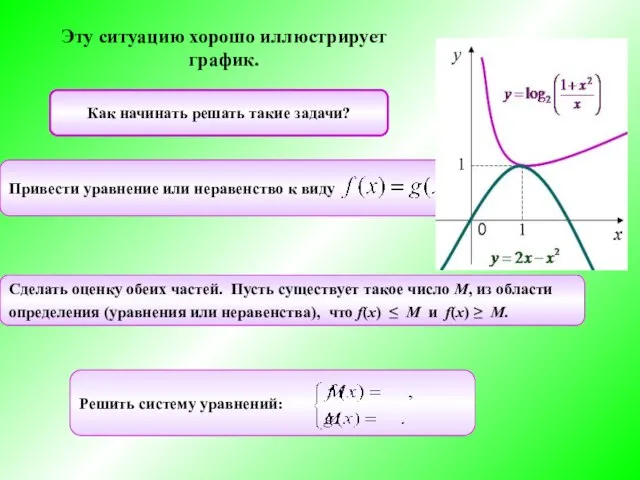
- 3. Определение Метод мажорант или метод оценки используется (чаще всего) в уравнениях вида f(x) = g(x) ,
- 4. Как начинать решать такие задачи? Сделать оценку обеих частей. Пусть существует такое число М, из области
- 5. Решение. Оценим обе части уравнения. При всех значениях х верны неравенства: Следовательно, данное уравнение равносильно системе:
- 6. Пример 2. Решить уравнение Решение: Оценим обе части уравнения. Следовательно, данное уравнение равносильно системе: При х
- 7. Пример 3. Решить неравенство тогда неравенство примет вид неравенство выполняется тогда и только тогда, когда Ответ:
- 8. Пример 4. Решить уравнение Для правой части (в силу неравенства для суммы двух взаимно обратных чисел)
- 9. Пример 5. Решить уравнение Поскольку - 1 ≤ sinx ≤ 1 и - 1 ≤ sin
- 10. Пример 6. Решить уравнение Решение. Очевидно, что почленно эти неравенства, получаем: Следовательно, левая часть равна правой,
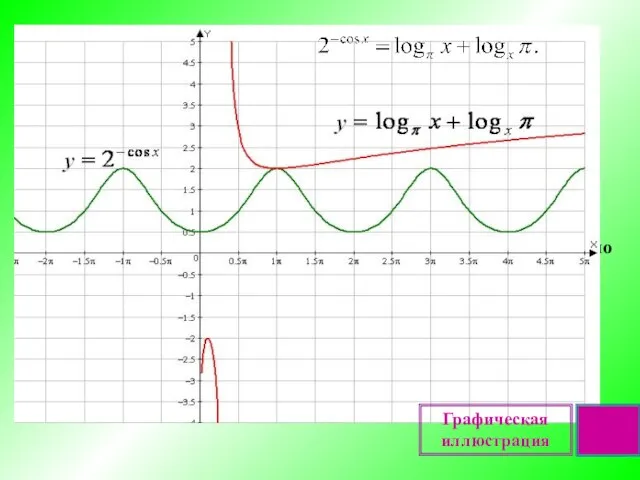
- 11. Проверим справедливость первого равенства, подставив эти корни: Пример 7. Решите уравнение Решение. Для решения уравнения оценим
- 13. Скачать презентацию


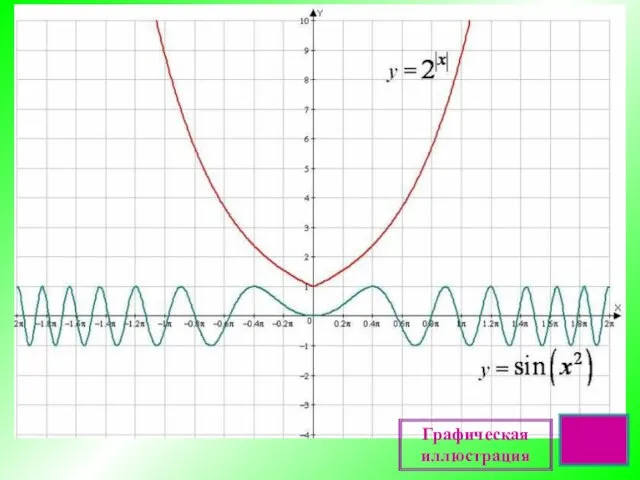
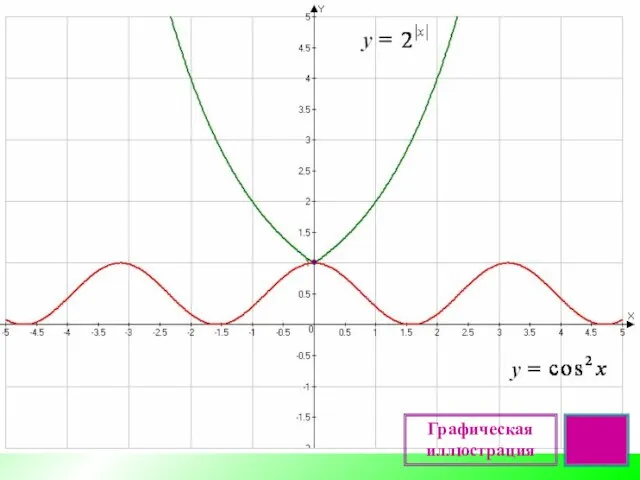
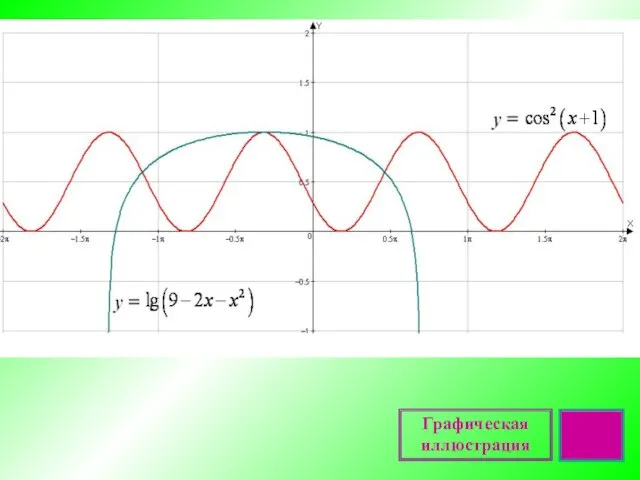



 Графики тригонометрических функций
Графики тригонометрических функций vzaimno-obratnye-funkcii.ppt
vzaimno-obratnye-funkcii.ppt Подготовка к ГИА. Алгебраические выражения
Подготовка к ГИА. Алгебраические выражения Презентация на тему Никола Тесла - человек из будущего
Презентация на тему Никола Тесла - человек из будущего  Построение арифметических выражений
Построение арифметических выражений Приращение аргумента. Приращение функции
Приращение аргумента. Приращение функции Решение систем линейных уравнений с двумя неизвестными
Решение систем линейных уравнений с двумя неизвестными Радианная мера углов и дуг
Радианная мера углов и дуг Презентация на тему Предпосылки возникновения философии в эпоху Возрождения
Презентация на тему Предпосылки возникновения философии в эпоху Возрождения  Алгебра и начала анализа
Алгебра и начала анализа Логарифмы. Логарифмическая функция 10 класс
Логарифмы. Логарифмическая функция 10 класс Исследование математических моделей
Исследование математических моделей  Наглядное представление статистической информации
Наглядное представление статистической информации Презентация на тему Отечественная психологическая мысль
Презентация на тему Отечественная психологическая мысль  Преобразование графиков функций
Преобразование графиков функций Развитие логического мышления у детей дошкольного возраста c речевыми нарушениями
Развитие логического мышления у детей дошкольного возраста c речевыми нарушениями Методы решения иррациональных уравнений Автор: Макарова Татьяна Павловна, учитель математики высшей категории ГБОУ СОШ №618 г.
Методы решения иррациональных уравнений Автор: Макарова Татьяна Павловна, учитель математики высшей категории ГБОУ СОШ №618 г.  Стандартный вид многочлена
Стандартный вид многочлена Сумма бесконечной геометрической прогрессии
Сумма бесконечной геометрической прогрессии  Тізімдер мен кестелер
Тізімдер мен кестелер Числовые промежутки 7 класс
Числовые промежутки 7 класс pervoobraznaya-i-neopredelennyy-integral.pptx
pervoobraznaya-i-neopredelennyy-integral.pptx Степень с рациональным показателем Действия со степенями
Степень с рациональным показателем Действия со степенями  Арифметика десятичных дробей
Арифметика десятичных дробей Теорема Виета (8 класс)
Теорема Виета (8 класс) Неполные квадратные уравнения
Неполные квадратные уравнения Презентация на тему Рынок недвижимости
Презентация на тему Рынок недвижимости  Презентация на тему Монизм, дуализм плюрализм в трактовке Бытия
Презентация на тему Монизм, дуализм плюрализм в трактовке Бытия